形态学算法应用之连通分量提取的python实现——图像处理

原理

连通分量提取是图像处理和计算机视觉中的一项基本任务，旨在识别图像中所有连通区域，并将它们作为独立对象处理。在二值图像中，连通分量通常指的是所有连接在一起的前景像素集合。这里的“连接”可以根据四连通或八连通的邻接关系来定义。

连通分量提取的基本原理
邻接关系：

四连通：一个像素仅与其上、下、左、右四个邻域像素相连。
八连通：一个像素与其上、下、左、右以及四个对角线方向的邻域像素相连。
扫描算法：连通分量的提取通常通过扫描整个图像，对每个前景像素检查其邻域，以确定它是否属于已知的连通分量，或需要创建一个新的连通分量。这个过程可以使用两种主要技术：

基于标签的扫描：在第一次扫描过程中，为图像中的每个像素分配一个临时标签，表示其所属的连通分量。如果一个像素与一个或多个已标记的像素相连，它将被赋予相同的标签。如果相连的像素属于不同的连通分量，则需要在后续处理中合并这些分量。第二次扫描中，所有属于同一连通分量的像素将被赋予一个唯一的标签。
并查集（Union-Find）算法：这是一种有效的数据结构和算法，用于跟踪元素分组的集合。在连通分量提取的过程中，它可以用来合并相交的连通分量，并快速查找某个像素所属的连通分量。
数学形态学在连通分量提取中的应用
数学形态学提供了一组用于图像处理的工具，特别是对图像进行膨胀、腐蚀、开操作和闭操作，这些都是基于结构元素的形状操作。在连通分量提取中，可以利用膨胀和腐蚀操作来改善连通分量的识别：
腐蚀：可以用来去除小的噪声点，可能有助于分离在原始图像中紧密相连的对象。
膨胀：可以用来填补对象内的小孔，或将靠得很近的对象连接起来。
应用
连通分量提取广泛应用于图像分割、对象识别、目标跟踪和图像分类等领域。通过识别和标记图像中的独立对象，可以进一步对每个对象进行分析，如计算它们的大小、形状、位置等特性，这对于理解图像内容和进行高级图像分析至关重要。

python实现下图

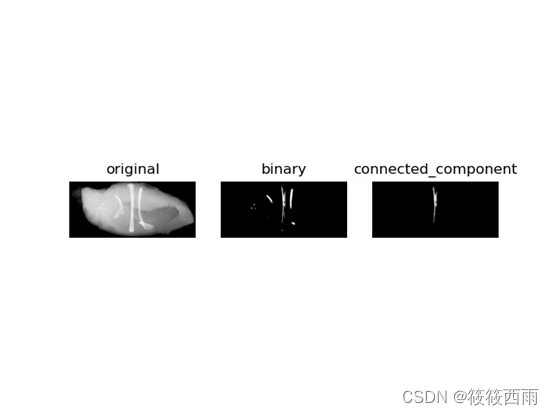
提示

结果图显示了对该图提取其中一个连通分量的结果。
第一步，用阈值210对原图进行阈值操作，得到二值图像，可用函数cv2.threshold(img, 210, 1, cv2.THRESH_BINARY)实现；
第二步，指定一个连通分量的起始位置（实验中取坐标(100, 350)），构造初始阵列X_0（除了(100,350)位置置1，其余位置置0）；
第三步，按照公式X_k=〖(X〗(k-1)⊕B)∩A,k=1,2,3,…更新阵列，直到X_k=X(k-1)，其中B是5×5的方形结构元.最后收敛后的X_k即为上图最右显示的一个连通分量。

python代码

import cv2
import numpy as np
import matplotlib.pyplot as plt

start_position=(100,350)  #(90,400)
img = cv2.imread('Fig0918.tif', 0)
_, img_bin = cv2.threshold(img, 210, 1, cv2.THRESH_BINARY)
kernel = np.ones((5, 5), dtype=np.uint8)
img_dst = np.zeros(img.shape)
img_dst[start_position] = 1
img_last = np.zeros(img.shape)

while (np.sum(img_dst-img_last) != 0):
    img_last = img_dst
    img_dst = cv2.dilate(img_last, kernel)
    img_dst = np.logical_and(img_dst, img_bin)
    img_dst = img_dst.astype(np.float)

plt.subplot(1,3,1)
plt.imshow(img,cmap='gray')
plt.axis("off")
plt.title("original")

plt.subplot(1,3,2)
plt.imshow(img_bin,cmap='gray')
plt.axis("off")
plt.title("binary")
plt.subplot(1, 3, 3)
plt.imshow(img_dst, cmap='gray')
plt.axis('off')
plt.title('connected_component')

plt.show()

此代码是从一个指定的起点开始，通过迭代膨胀和逻辑与操作，识别和提取与该点连通的图像区域。这种方法特别适用于分析和处理具有复杂形状或结构的图像，在图像分割、目标识别等领域有着广泛的应用。

结果展示

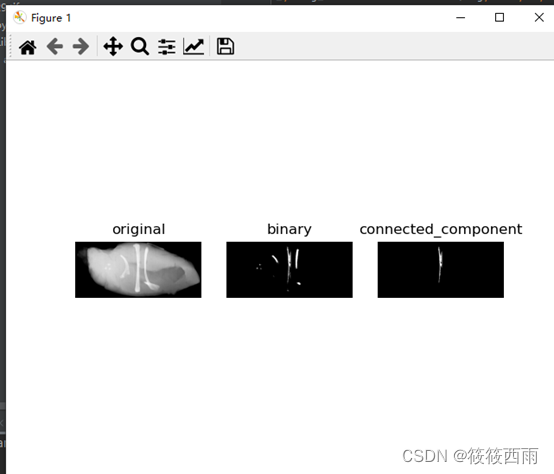
取坐标(90, 400), 可以提取出另一根骨头。

总结

连通分量的定义：令S是一个像素子集，如果S中的全部像素之间存在一个通路（m通路或8通路），则可以说两个像素p和q在S中是连通的。对于S中的任何像素p，S中连通到该像素的像素集称为S的连通分量。
应用背景：在许多自动图像分析应用中，如何识别出图像中的不同之处，往往是从其二值图像中提取连通分量。

流程：
第一步，用阈值210对原图进行阈值操作，得到二值图像，可用函数cv2.threshold(img, 210, 1, cv2.THRESH_BINARY)实现；
第二步，指定一个连通分量的起始位置（实验中取坐标(100, 350)），构造初始阵列X_0（除了(100,350)位置置1，其余位置置0）；
第三步，按照公式X_k=〖(X〗(k-1)⊕B)∩A,k=1,2,3,…更新阵列，直到X_k=X(k-1)，其中B是5×5的方形结构元.最后收敛后的X_k即为上图最右显示的一个连通分量。