「递归算法」:子集(两种解法)
一、题目
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3] 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0] 输出:[[],[0]]
二、思路解析
解法一
来看看这道题的决策树模型,下图的 × 代表不选择该元素,✓ 代表选择,所有叶子节点均为答案。

而这种方法,需要一个 pos 变量,用于记录已经遍历过的元素个数。
当遍历个数和 nums 数组的大小一致时,则为函数出口,把一次遍历也插入到 ret 变量中,然后直接返回即可。
函数体部分代码也较为简单,剪枝我也在前面出过一期博客,在此不做讲解。
第一种解法的所有叶子结点均为符合题意的答案。
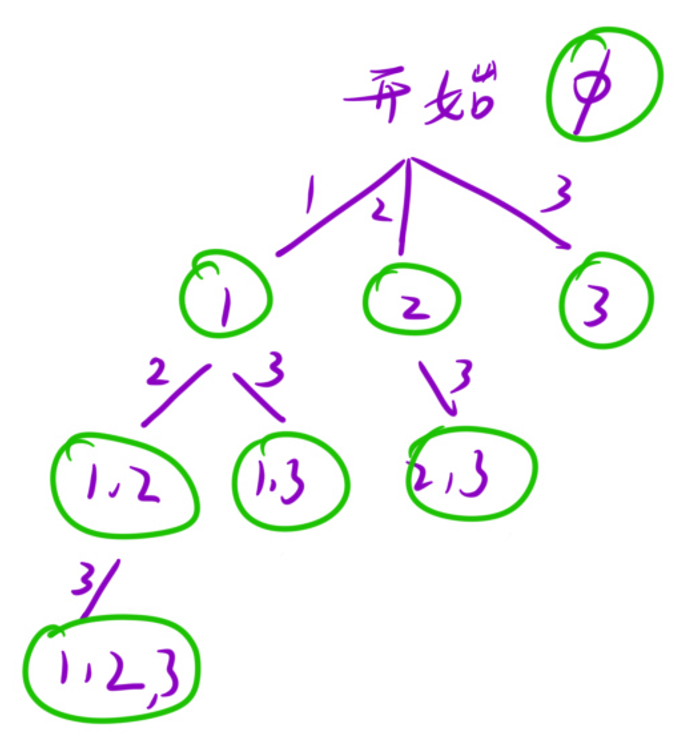
解法二
和解法一的区别,主要在于解法二用了一个 for 循环来遍历数组,且在循环中再次递归调用。
但是在这种解法,我们不再判断选与不选,而是把当前元素及其后面的每个元素都统计在内。
这样的结果,就是所有节点均为满足题意的答案,也就是图中绿色部分元素。
三、完整代码
解法一:
class Solution {
List<List<Integer>> ret;
List<Integer> path;
public List<List<Integer>> subsets(int[] nums) {
ret = new ArrayList<>();
path = new ArrayList<>();
dfs(nums , 0);
return ret;
}
public void dfs(int[] nums , int pos){
// 解法一
if(pos == nums.length){
ret.add(new ArrayList<>(path));
return;
}
// 选
path.add(nums[pos]);
dfs(nums , pos + 1);
path.remove(path.size() - 1);
// 不选
dfs(nums , pos + 1);
}解法二:
class Solution {
List<List<Integer>> ret;
List<Integer> path;
public List<List<Integer>> subsets(int[] nums) {
ret = new ArrayList<>();
path = new ArrayList<>();
dfs(nums , 0);
return ret;
}
public void dfs(int[] nums , int pos){
// 解法二
ret.add(new ArrayList<>(path));
for(int i = pos ; i < nums.length ; i ++){
path.add(nums[i]);
dfs(nums , i + 1);
path.remove(path.size() - 1);
}
}以上就是本篇博客的全部内容啦,如有不足之处,还请各位指出,期待能和各位一起进步!
