经典排序算法
文章目录
- 序言
- 算法分类
- 算法复杂度
- 1、交换排序
- 1.1 冒泡排序(Bubble Sort)
- 1.2 快速排序(Quick Sort)
- 2、选择排序
- 2.1 直接选择排序
- 3、插入排序
- 3.1 直接插入排序
- 3.2 希尔排序
- 4、归并排序
序言
算法分类
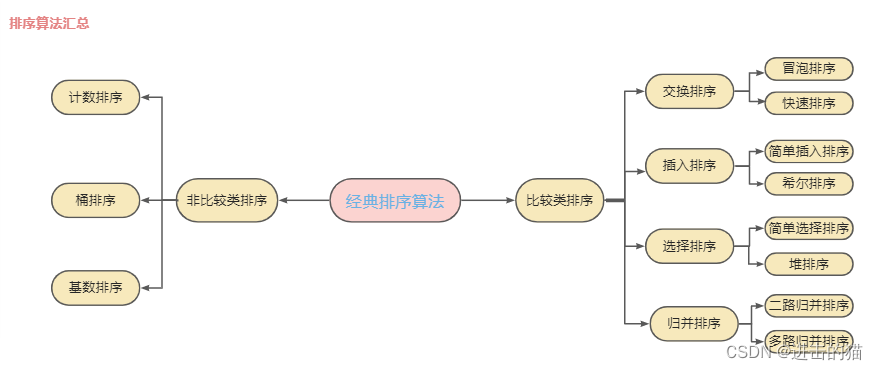
排序算法可以分为两大类:
- 比较类排序:通过相互比较来决定各元素之间的顺序,由于其时间复杂度不能突破O(nlogn),即非线性时间比较类排序。主要包含交换排序、插入排序、选择排序和归并排序;
- 非比较类排序:不通过比较来决定元素间的顺序,它可以突破基于比较排序的时间下界,以线性时间运行,即线性时间非比较类排序。主要包含计数排序、桶排序和基数排序;
算法复杂度
| 排序算法 | 时间复杂度(平均) | 时间复杂度(最差) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n2) | O(n) | O(1) | 稳定 |
| 快速排序 | O(n㏒2n) | O(n2) | O(n㏒2n) | O(n㏒2n) | 不稳定 |
| 简单插入排序 | O(n2) | O(n2) | O(n) | O(1) | 稳定 |
| 希尔排序 | O(n1.3) | O(n2) | O(n) | O(1) | 不稳定 |
| 简单选择排序 | O(n2) | O(n2) | O(n2) | O(1) | 不稳定 |
| 堆排序 | O(n㏒2n) | O(n㏒2n) | O(n㏒2n) | O(1) | 不稳定 |
| 归并排序 | O(n㏒2n) | O(n㏒2n) | O(n㏒2n) | O(n) | 稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(n+k) | 稳定 |
| 桶排序 | O(n+k) | O(n2) | O(n) | O(n+k) | 稳定 |
| 基数排序 | O(n2k) | O(n2k) | O(n2k) | O(n+k) | 稳定 |
稳定性: 排序过程中,相等的两个值对比时是否会发生前后变化。
- (1)稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
- (2)不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
时间复杂度: 对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
空间复杂度: 是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
1、交换排序
1.1 冒泡排序(Bubble Sort)
描述:
冒泡排序 是一种简单的排序算法。重复遍历需要排序的数列,每次比较两个元素,按照升序或降序的方式交换位置,直到没有再需要交换的值,即该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
图形效果:
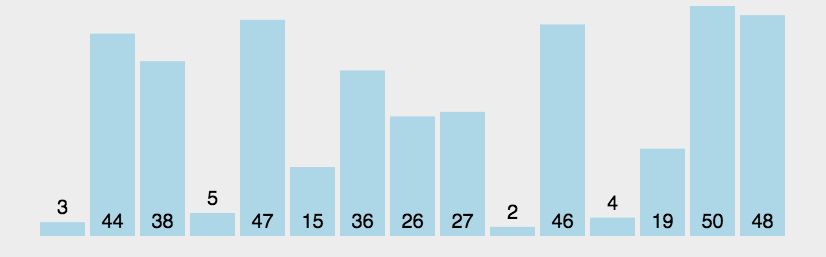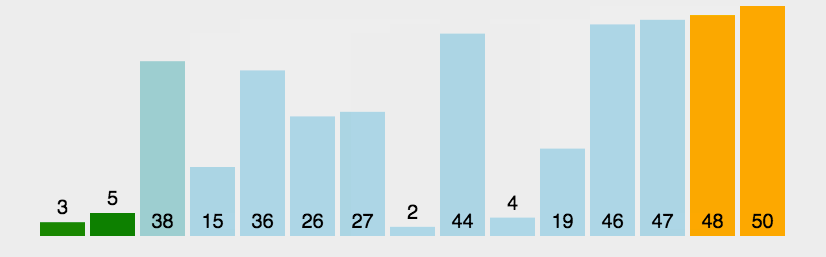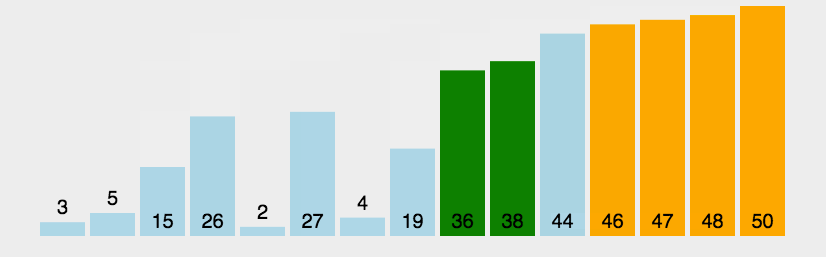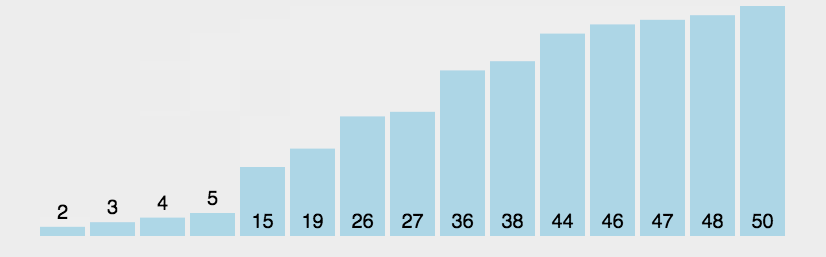
设计思想(分治法)::
使用双重循环遍历该数组,外层循环控制遍历次数,内层循环每个位置相互比较,按照升序或降序的规则,对比时小的或大的数值将被放在前面或后面。
性能:
- 时间复杂度:最好时间:O(n) 最坏:O(n2) 平均:O(n2)
- 辅助空间:O(1)
- 稳定性:稳定
代码实现:
/**
* 交换排序:冒泡排序
* @param array
* @return
*/
public static int[] bubbleSort(int[] array){
for (int i = 0; i < array.length; i++) {//外层循环控制遍历的位置数量
for (int j = 0; j < array.length - i - 1; j++) {//内层循环对比是否交换位置
if(array[j] > array[j+1]){
int tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
}
}
}
return array;
}
1.2 快速排序(Quick Sort)
描述:
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分割结束之后,对基准值的排序就已经完成;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
图形效果:
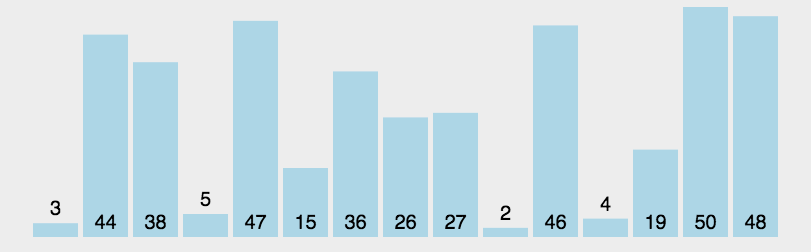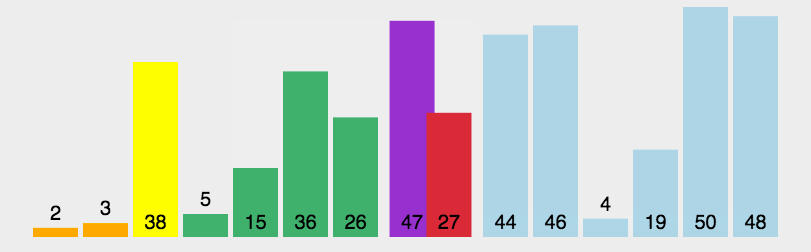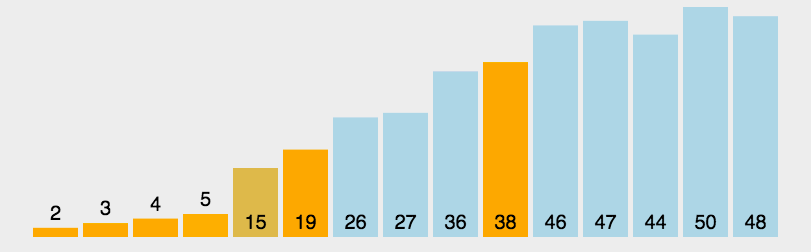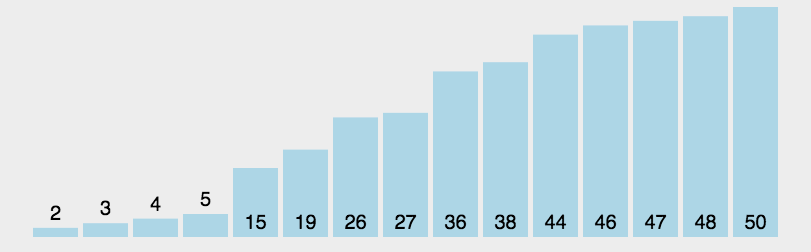
设计思想(分治法):
- (1)对于一组给定的记录,通过一趟排序后,将原序列分为两部分,其中前一部分的所有记录均比后一个序列的记录小;
- (2)再依次对前后两部分的记录进行快速排序;
性能::
- 时间复杂度:最坏时间:O(n2); 最好和平均:O(n*log n)
- 辅助空间:O(log n)
- 稳定性:不稳定
代码实现:
/**
* 交换排序:快速排序
* 时间复杂度:最坏时间:O(n^2); 最好和平均:O(n*log n) 辅助空间:O(log n) 稳定性:不稳定
* @param array 待排序数组
* @return 排序后的数组
*/
public static int[] quickSort(int[] array) {
if(array!=null&&array.length>0){
quickSorts(array,0,array.length-1);
}
return array;
}
private static void quickSorts(int[] array, int low, int high){
//递归结束条件
if(low >= high){
return ;
}
//定义基准值
int key = array[low];
//从前往后遍历的索引坐标
int i = low;
//从后往前遍历的索引坐标
int j = high;
//从基准开始出发,i、j两个值从前和从后两个方向向中间遍历,直到相遇(交叉)即停止遍历,代表此次找到新的基准和分段排序
while(i < j){
//循环从后往前遍历获取比基准key小的值,记录下标j
while(i < j && array[j] > key){
j--;
}
//循环从前往后遍历获取比基准key大的值,记录下标i
while(i < j && array[i] <= key){
i++;
}
/**
* 找到基准key进行上述i和j的循环需要交换的值
* i为找到大于等于基准的下标索引
* j为找到小于基准的下标索引
* i大于等于j则表明不需要交换,不满足交换i、j条件
*/
if(i < j){
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
// 调整key的基准即
int temp = array[low];
array[low] = array[i];
array[i] = temp;
//排序i左边
quickSorts(array,low,i-1);
//排序i右边
quickSorts(array,i+1,high);
}
2、选择排序
2.1 直接选择排序
描述:
选择排序就是每次找未排序数组中的最小(最大)的记录并固定其位置。
图形效果:
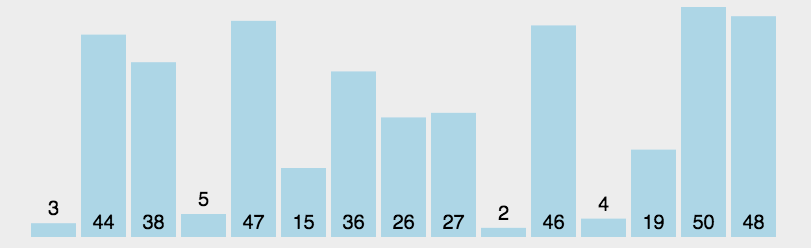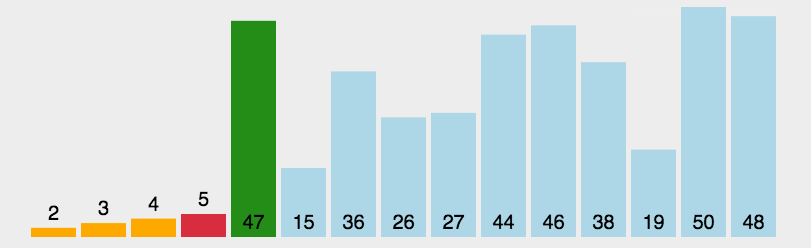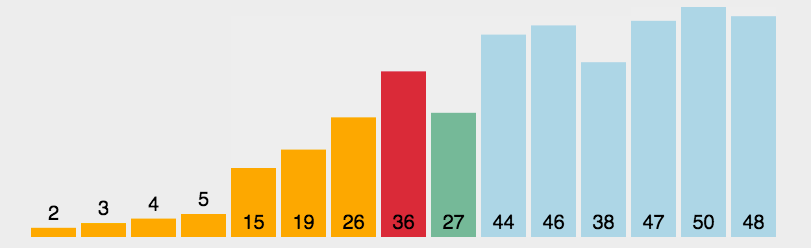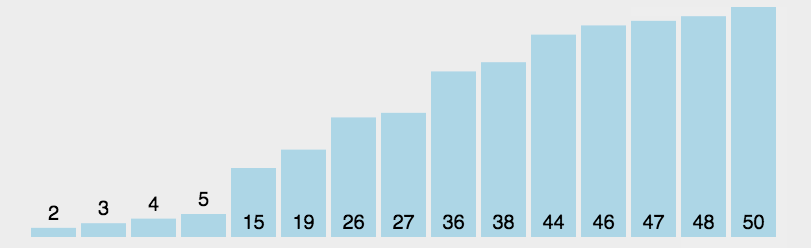
设计思想:
- (1)对于给定的一组记录,经过第一轮比较后得到最小的记录,然后将该记录与第一个记录的位置进行交换;
- (2)接着对不包括第一个记录之外的其他记录进行第二轮比较,得到最小的记录并与第二个记录进行位置交换;
- (3)重复该过程,直到全部排序
性能::
- 时间复杂度:最好和最坏的平均时间均为O(n2)
- 辅助空间:O(1)
- 稳定性:不稳定
代码实现:
/**
* 选择排序:直接选择排序
* 时间复杂度:最好和最坏平均时间均为O(n^2) 辅助空间:O(1) 稳定性:不稳定
* @param array
* @return
*/
public static int[] chooseSort(int[] array){
//控制外层循环即N次交换值,将剩余后的最小值与i位置交换
for(int i = 0; i < array.length - 1; i++){
//记录每次循环的最小值索引
int min = i;
//遍历找到每次循环的最小值
for(int j = i + 1; j < array.length; j++){
if(array[j] < array[min]){
//记录本次外层循环的最小值
min = j;
}
}
//将最小值和第i个位置进行对换
int temp = array[i];
array[i] = array[min];
array[min] = temp;
}
return array;
}
3、插入排序
3.1 直接插入排序
描述:
将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找并进行移动。
图形效果:
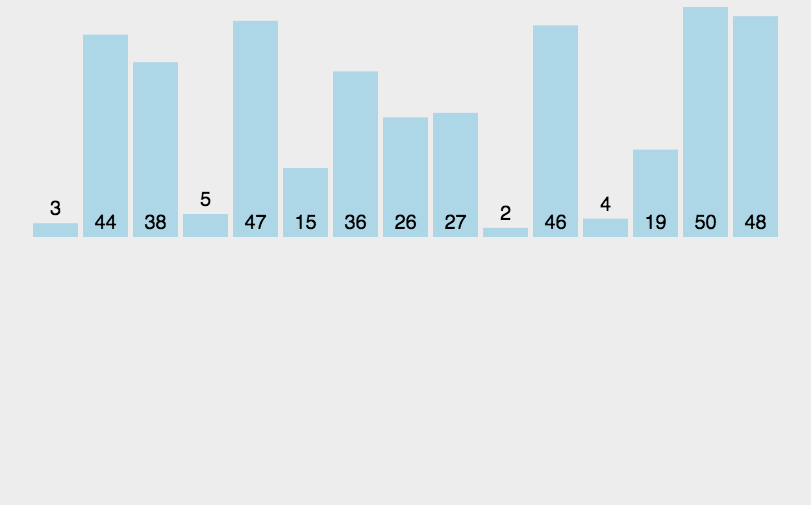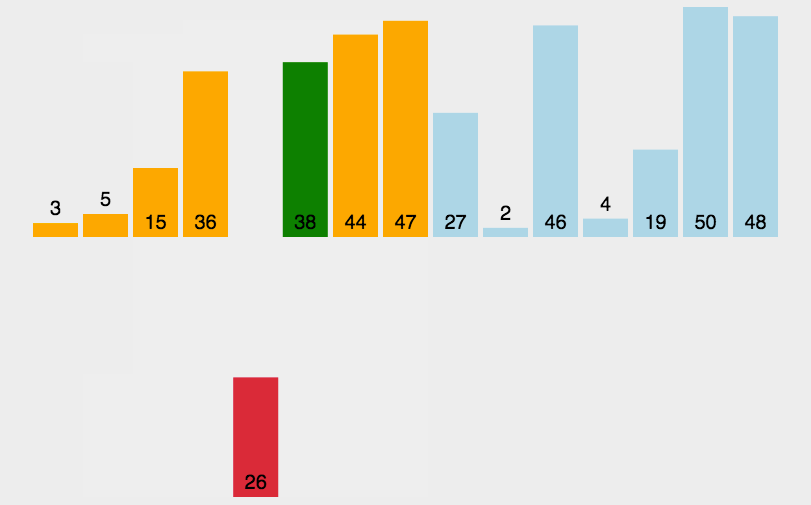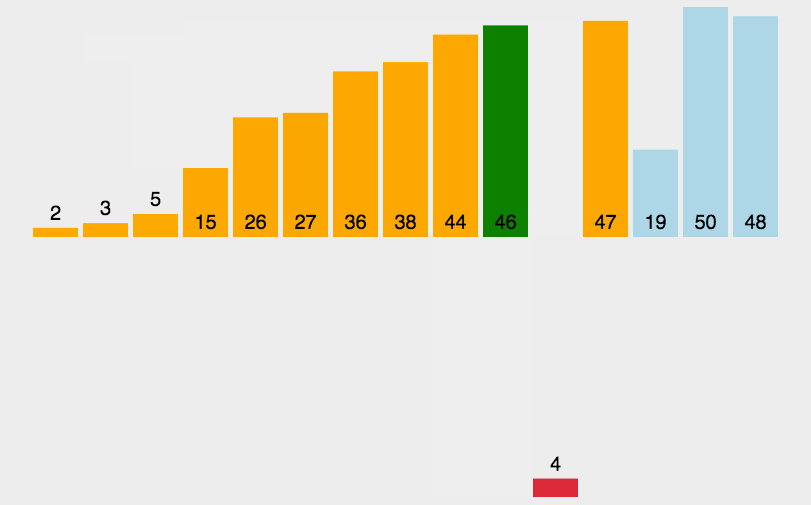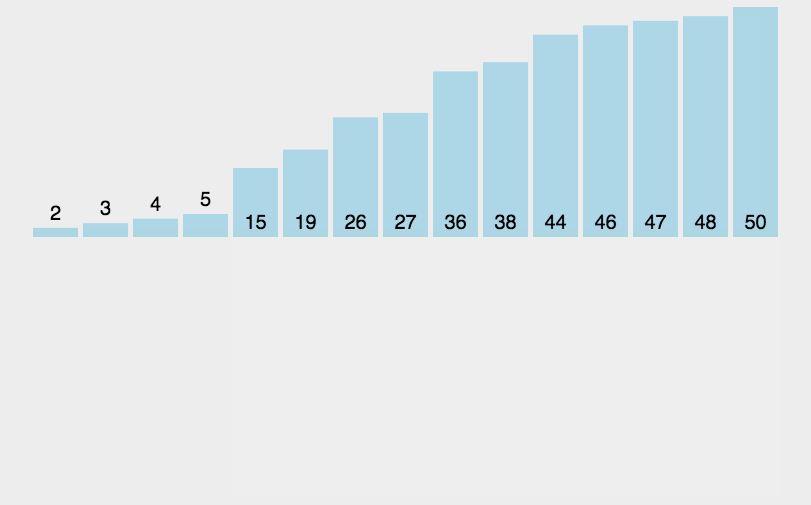
设计思想:
- 初始时假设第一个记录自成一个有序序列,其余记录均为无序序列;
- 接着从第二个记录开始,按照记录的大小依次将当前处理的记录插入到其之前的有序序列中;
- 直到最后一个记录插入到有序序列中为止;
性能::
- 时间复杂度:最好时间:O(n);最坏:O(n2) 平均:O(n2)
- 辅助空间:O(1)
- 稳定性:稳定
代码实现:
/**
* 插入排序:直接插入排序
* @param array
* @return
*/
public static int[] insertSort(int[] array){
//待插入的节点
int insertNode = 0;
//遍历索引
int leftIndex = 0;
//循环遍历,从数组中第二个节点开始,默认第一个节点是有序的即一个数字本身就是有序的
for(int i = 1; i < array.length; i++){
//循环设置插入值
insertNode = array[i];
//获取有序列表中的最右下标索引
leftIndex = i - 1;
/**
* 从有序列表中的最右下标索引开始与插入值对比
* 仅当下标索引不为负数才使用下标索引值对比插入值即索引仍在有序列表中
* 索引值大于插入值,则说明继续往左边遍历
*/
while(leftIndex >= 0 && array[leftIndex] > insertNode){
//移动有序列表中的值
array[leftIndex+1] = array[leftIndex];
//索引自减
leftIndex--;
}
/**
* 将插入值放入索引位置,因遍历初进行i-1,说明本身leftIndex是在i的左侧
* 若while循环未进入,也能保证leftIndex+1 等于i,相当于自身重复赋值
* 若满足while条件,则说明leftIndex又被减少过,即说明插入点索引也是需要加1
*/
array[leftIndex+1] = insertNode;
}
return array;
}
3.2 希尔排序
描述:
希尔排序也叫“缩小增量排序”,是插入排序的改进版
图形效果:

设计思想:
- 首先选择一个步长序列,t1=n/2, t2=t1/2, … ,tk=1;如n=10,则步长序列{5,2,1}
- 然后按步长序列个数k,对待排序序列进行k趟排序;
- 每趟排序,根据对应步长ti,将待排序列分成ti个子序列,分别对各个子序列进行直接插入排序。
性能::
- 时间复杂度:最坏平均:O(n*log n)或 O(n^1.25)
- 辅助空间:O(1)
- 稳定性:不稳定
代码实现:
/**
* 插入排序:希尔排序
* @param a 排序的数组
* @param n 排序的长度,用以确定步长序列{t1=n/2,t2=t1/2,...}
*/
public static void shellSort(int[] array,int n){
//获取步长
for (int gap = n/2; gap > 0 ; gap = gap/2) {
//对每一个步长,进行遍历,按步长对应的索引下标对比
for (int i = gap; i < n; i++) {
// 索引对应值对比
if(array[i] < array[i-gap]){
//存储步长目标值
int temp = array[i];
//获取步长的上一个索引下标
int k = i - gap;
/**
* 循环对比步长索引值即关键遍历步长对比
* (1)每次对比必须步长前索引值大于目标索引值才进行赋值
* (2)每次进行赋值后,需要对步长对比索引向前推进步长单位,然后再次进行对比
* (3)直到对比索引越界后结束或对比索引值与目标索引小,则结束while循环
*/
while (k >= 0 && array[k] > temp){
//将目标值小于对比索引值的进行赋值即将小值放在前一个步长
array[k+gap] = array[k];
//继续按步长进行推进,再次对比,检查是否需要继续向前对比
k -= gap;
}
//将步长目标值设置到原位置或上述while变更的位置
array[k+gap] = temp;
}
}
}
}
4、归并排序
描述:
将待排序列使用递归进行折半分组,使用辅助数组按照从小到大进行两两合并;
图形效果:
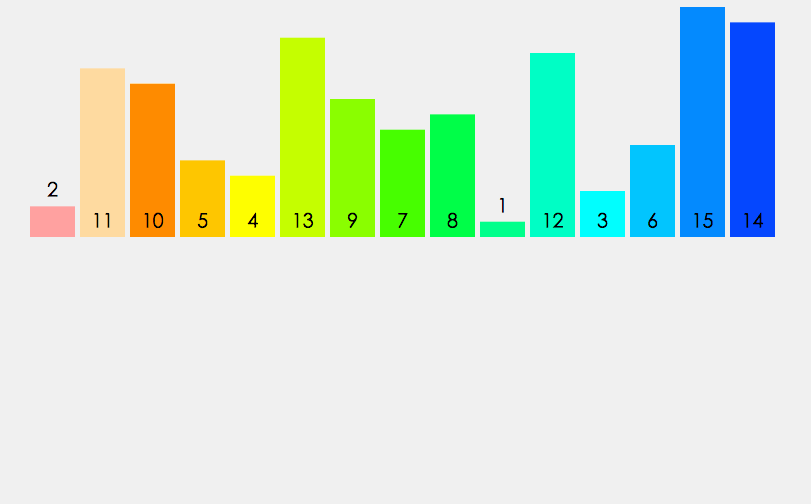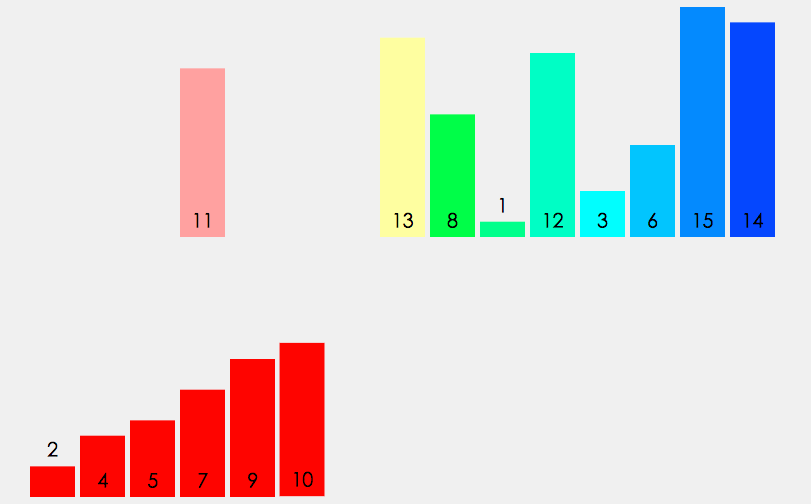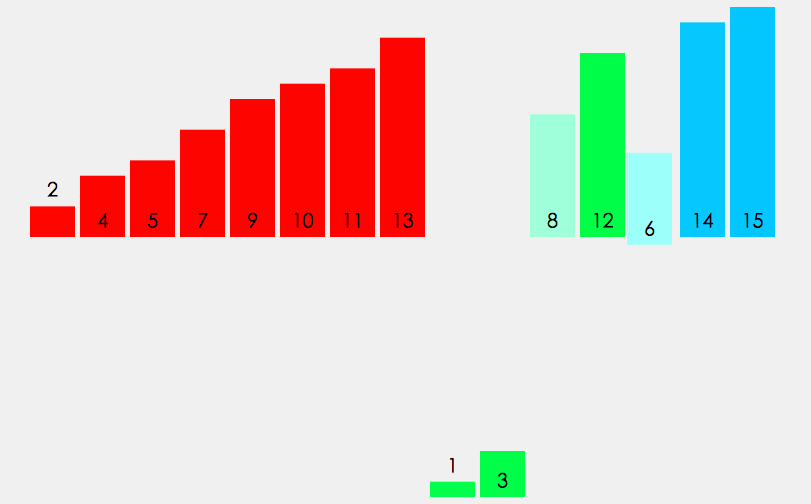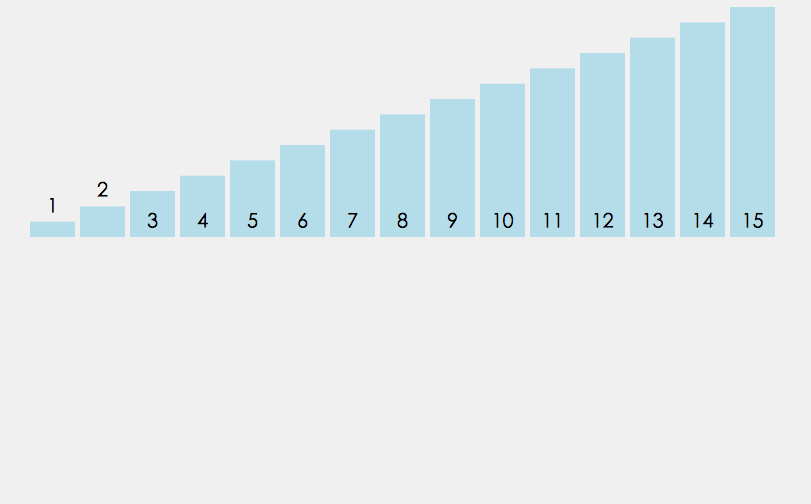
设计思想:
利用递归与分治技术将数据序列划分为越来越小的半子表,再对半子表排序,最后用递归将排好序的半子表合并为越来越大的有序序列。
- (1) “归”–表示递归,即递归将数组折半地分为单个数组;
- (2) “并”–表示合并,即将分开的数据按照从小到大或从大到小的顺序再放到一个数组中;
- (3)对于给定一组记录,首先将每两个相邻的长度为1的子序列进行归并,得到【n/2】(向上取整)个长度为2或者1的有序子序列,再将其两两归并;反复执行此过程直到得到一个有序序列;
性能:
- 时间复杂度:最好、最坏、平均时间:O(n*log n)
- 辅助空间:O(n)
- 稳定性:稳定
实现代码:
/**
* 2.二路归并排序,递归实现
* @param array 待排序数组
* @param first 起点
* @param last 终点
* @param temp 辅助数组
*/
public static void mergeSort(int[] array,int first,int last,int[] temp){
//二路排序递归终止条件
if(first >= last){
return ;
}
//获取本次需要排序的起点和终点的中间点
int mid = (first + last)/2;
//开启中间点左边排序即一路
mergeSort(array,first,mid,temp);
//开启中间点右边排序即另一路
mergeSort(array,mid+1,last,temp);
//对上述两路排序进行合并排序
mergeArray(array,first,mid,last,temp);
}
/**
* 1.将两个有序数组进行合并,a[first,mid] 和 a[mid+1,last]
* @param array 待排序数组
* @param first 起点
* @param mid 中间点
* @param last 终点
* @param temp 辅助数组
*/
public static void mergeArray(int[] array,int first,int mid,int last,int[] temp){
//定义第一路即中间点左边数组起始点
int i = first;
//定义第二路即中间点右边数组起始点
int j = mid + 1;
//定义辅助数组起始点
int k = 0;
//循环遍历两路,将小值陆续放入辅助数组
while (i <= mid && j <= last){
//左路与右路遍历对比
if(array[i] <= array[j]){
//放入辅助数组
temp[k++] = array[i++];
}else {
//放入辅助数组
temp[k++] = array[j++];
}
}
//检查上面while不满足条件时是否存在左路未遍历完
while (i <= mid){
temp[k++] = array[i++];
}
//检查上面while不满足条件时是否存在右路未遍历完
while (j <= last){
temp[k++] = array[j++];
}
for (int s = 0;s < k;s++) {
array[first+s] = temp[s];
}
}
