回溯算法大致分为以下几类：
组合：组合、组合总和、电话号码的字母组合
分割：分割回文串、复原IP地址
子集：子集
排列：全排列
棋盘问题：N皇后、解数独
其他：递增子序列、重新安排行程

一、什么是回溯算法

回溯算法也可以叫做回溯搜索法，它是一种搜索方法。
回溯是递归的副产品，只要有递归就会有回溯（递归中隐藏着回溯算法）。
所以以下讲解中，回溯函数也就是递归函数，指的都是一个函数。

二、回溯算法解决什么问题

回溯算法，一般可以解决如下几种问题：

• 组合问题：N个数里面按一定规则找出K个数的集合
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 排列问题：N个数按一定规则全排列，有多少种排列方式
• 棋盘问题：N皇后，解数独等

这里再帮大家回顾一下高中的排列组合知识。
组合和排列的区别是，组合是不强调元素顺序的，而排列强调元素顺序。
举个最简单的例子：[1,2]这个集合，论组合只有[1,2]这一个集合，论排列却有[1,2]、[2,1]这两个集合。

三、如何理解回溯算法

回溯法解决的问题都可以抽象成树形结构，因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，构成了树的深度。递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

四、回溯算法模板

1、回溯函数模板返回值以及参数

回溯算法中函数返回值一般为void。再来看一下参数，因为回溯算法需要的参数不像二叉树递归的时候那么容易一次性确定下来，所以一般先写逻辑，然后需要什么参数，就填什么参数。
回溯函数伪代码如下：

void backtrack(参数)

2、回溯函数终止条件

回溯法是一种树形结构，那么一定就会有终止条件。
什么时候达到了终止条件，树中就可以看出，一般来说搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。
所以回溯函数终止条件伪代码如下：

if (终止条件) {
    存放结果;
    return;
}

3、回溯搜索的遍历过程

回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成了树的深度。
如下图：

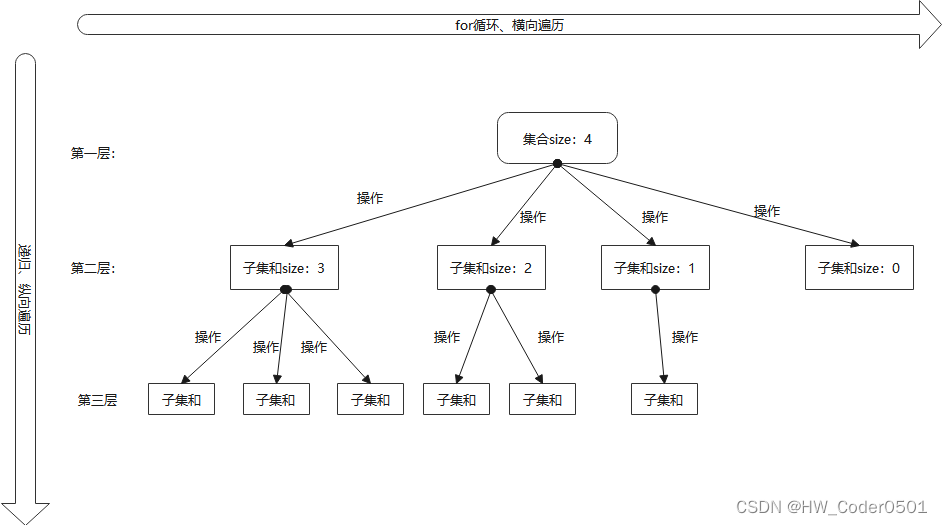
图中特意举例集合大小和孩子数量相等。
回溯函数遍历过程伪代码如下：

for (选择：本层集合中元素(树中节点孩子的数量就是集合的大小)) {
    处理节点;
    backtrack(路径， 选择列表);  // 递归
    回溯，撤销处理结果
}

for循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个for循环就执行多少次。
backtrack这里自己调用自己，实现递归。
可以从图中看出for循环可以理解是横向遍历，backtrack是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜到的叶子节点就是找的其中的一个结果了。
分析完过程，回溯算法模板框架如下：

void backtrack(参数)
if (终止条件) {
    存放结果;
    return;
}
for (选择：本层集合中元素(树中节点孩子的数量就是集合的大小)) {
    处理节点;
    backtrack(路径， 选择列表);  // 递归
    回溯，撤销处理结果
}

五、回溯算法效率

虽然回溯法很难，很不好理解，但是回溯法并不是什么高效的算法。
因为回溯的本质是穷举，穷举所有的可能，然后选出我们想要的答案，如果想要回溯法高效一些，可以加一些剪枝的操作，但这也改变不了回溯法就是穷举的本质。
那么，既然回溯法并不高效，为什么还要用它呢？因为对于某些问题来讲，只能使用暴力搜索来解决，除此之外没有更高效的解决方法。

六、回溯算法例题

以LeetCode第46题为例来讲解一下回溯算法的具体应用。

46. 全排列
给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]
示例 3：

输入：nums = [1]
输出：[[1]]
 
提示：
1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同

这个问题是典型的回溯递归问题，可用如下代码解答：

void swap(int * nums,int index1,int index2)
{
    int temp = nums[index1];
    nums[index1] = nums[index2];
    nums[index2] = temp;
}

void backTrack(int* nums, int numsSize, int* returnSize, int** returnColumnSizes, int** res, int offset)
{
    if(offset == numsSize) {  // 遍历到了末尾
        res[*returnSize] = (int *)malloc(sizeof(int ) * numsSize);
        memcpy(res[*returnSize], nums, sizeof(int) * numsSize );  // 拷贝结果到res中保存
        (*returnColumnSizes)[*returnSize] = numsSize;  // 记录返回数组中每行的列数
        *returnSize = *returnSize + 1;
    } else {
        //回溯算法的核心
        for(int i = offset; i < numsSize; i++) {
            swap(nums, i, offset);  // i 和 offset 交换，如[1,2,3]填入res后，此时步步回溯后，二次循环i为2，off为1，交换后为[1,3,2]
            backTrack(nums, numsSize, returnSize, returnColumnSizes, res, offset+1);
            swap(nums, i, offset);  // 从prem返回之后，也即找到一个答案后，将数组恢复为原来状态，在原状基础上继续遍历，如[1,3,2]填入res后恢复为[1,2,3]
        }
    }
}

int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes)
{
    //不重复的数字的全排序
    //组合次数为 n！= n *( n - 1) *( n - 2) ...... 2 * 1
    //这样的方法适合回溯的方法
    //取值范围1 <= nums.length <= 6  = 6 * 5 * 4 * 3 *2 * 1 = 720中可能
    int **res = (int **)malloc(sizeof(int *) * 721);
    *returnColumnSizes = (int *)malloc(sizeof(int ) * 721);
    *returnSize = 0;
    backTrack(nums, numsSize, returnSize, returnColumnSizes, res, 0);
    return res;
}