当前位置： 首页 > article >正文

动态规划题目集一（代码 注解）

article 2025/1/24 2:17:41

目录

 介绍：

题目一: 

 题目二：

 题目三：

 题目四：

 题目五：

 题目六：

 题目七：

 题目八：

题目九：

 介绍：

动态规划是一种算法设计技术，用于解决具有重叠子问题和最优子结构特征的问题。它通过将大问题拆分成小问题，并保存每个小问题的解以避免重复计算，从而提高算法的效率。

在动态规划中，问题可以通过子问题的最优解来构建整体问题的最优解。动态规划的核心思想是利用已解决的子问题的解来构建更大规模问题的解，以此递推得到最优解。

动态规划通常包含以下三个步骤：
1. 定义问题的状态：将问题划分为若干个子问题，并确定状态变量表示子问题的解。
2. 定义状态转移方程：通过递推关系式，将大问题的解表示为小问题的解。
3. 定义边界条件：确定问题的初始状态，即最小规模的子问题的解。通常是一些边界情况。

动态规划适用于那些具有重叠子问题和最优子结构特征的问题，例如最长公共子序列、背包问题、最短路径等。通过利用动态规划，我们可以将问题的时间复杂度从指数级别降低到多项式级别，从而提高算法的效率。

题目一: 

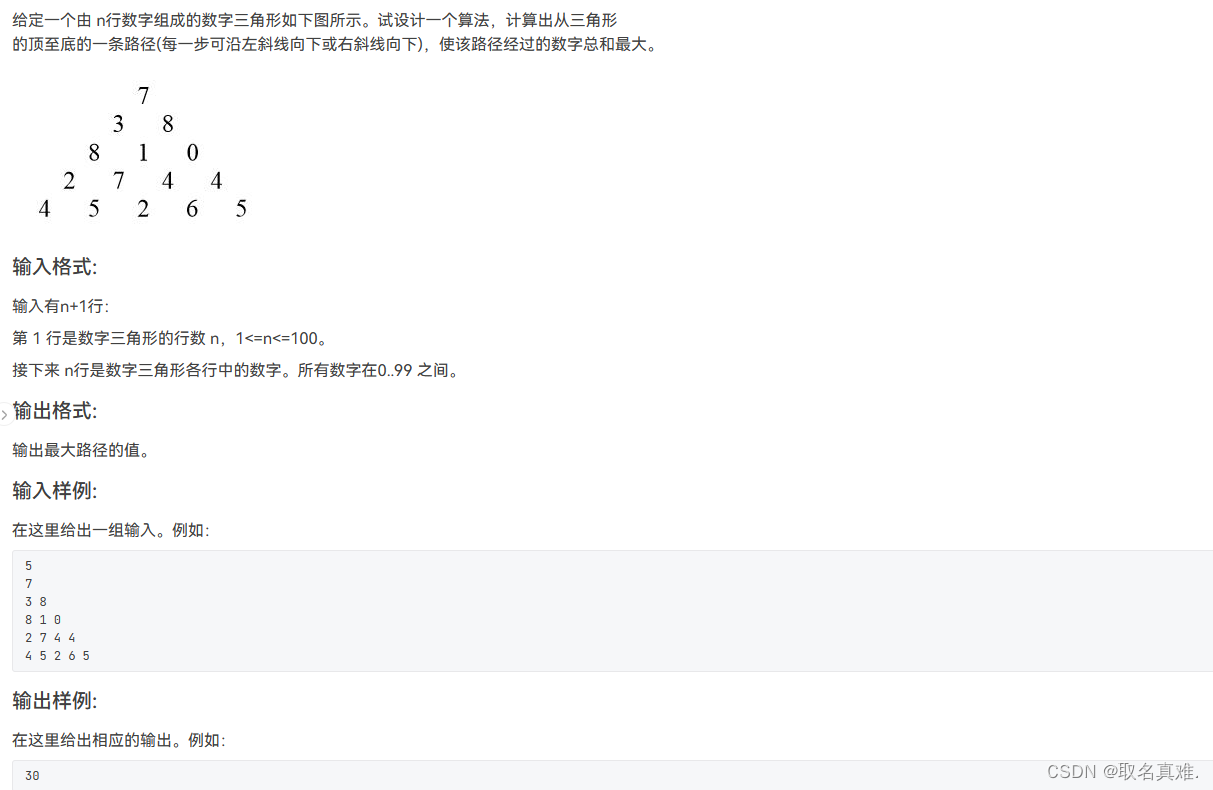
#include<iostream>
#include<cstring>
using namespace std;
int main()
{
    long long a[110][110];//第i行第j个可取的最大值
    int n;
    long long ans = 0;
    cin >> n;
    memset(a, 0, sizeof(a));
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= i; j++)
        {
            cin >> a[i][j];
            a[i][j] += max(a[i - 1][j], a[i - 1][j - 1]);//正上方的和斜上角的取大的加
            ans = max(ans, a[i][j]);
        }
    }
    cout << ans;
}

 题目二：

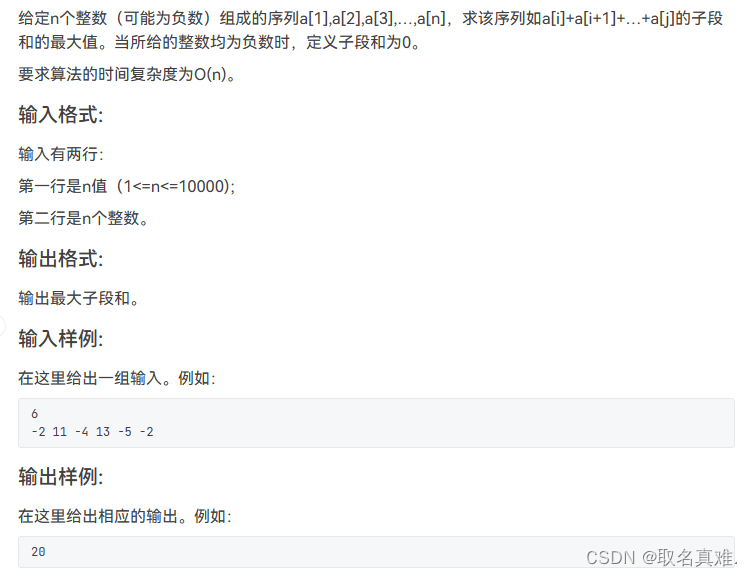
#include<iostream>
#include<cstring>
using namespace std;
int n;
int a[100100];
int f[100100];//以第j个结尾的最大子段和
int ans = 0;
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
    }
    f[1] = a[1];//第一个就为第一个的值
    for (int i = 2; i <= n; i++)
    {
        f[i] = max(f[i - 1] + a[i], a[i]);//比较i-1子段和加上当前的数是否大于当前数
        ans = max(ans, f[i]);
    }

    cout << ans << endl;

}

 题目三：

#include<iostream>
#include<cstring>
using namespace std;
int n;
int a[300][300];//i站到j站的租金
int f[300];//到j站的最少的租金
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		for (int j = i + 1; j <= n; j++)
		{
			cin >> a[i][j];
		}
	}
	for (int i = 1; i <= n; i++)
	{
		for (int j = i + 1; j <= n; j++)
		{
            if(i==1)
                f[j]=a[i][j];//每站初始为1直接到各个站
            else
			    f[j] = min(f[j], f[i] + a[i][j]);//选i为中转站，不选继承，选了则f[i]+a[i][j]
		}
	}
	cout << f[n] << endl;
}

 题目四：

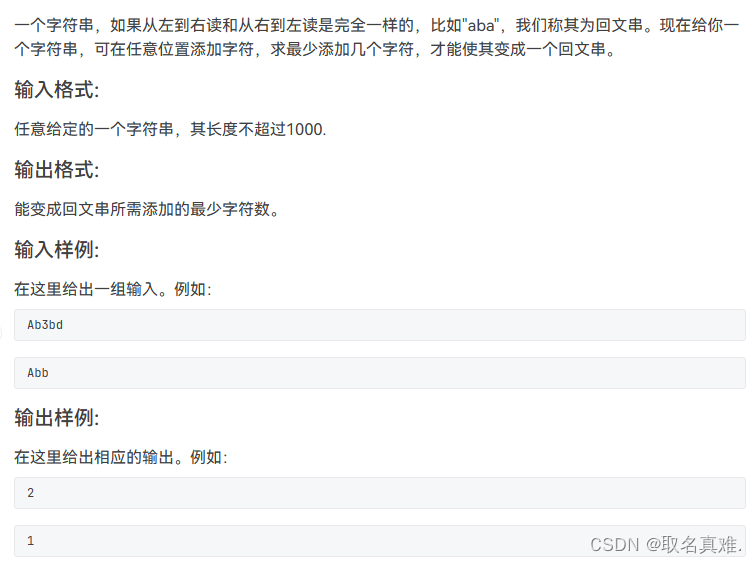
#include<iostream>//求翻转字符串和原字符串的公共子序列
#include<algorithm>
#include<cstring>
using namespace std;
string str, str1;
int dp[1001][1001];//表示到str字符串的第i个与str1字符串的第j个有的最长公共子序列
int main()
{
    memset(dp, 0, sizeof(dp));
    cin >> str;
    int len = str.length();
    str1 = str;
    reverse(str.begin(), str.end());//翻转
    for (int i = 1; i <= len; i++)
    {
        for (int j = 1; j <= len; j++)
            if (str[i - 1] == str1[j - 1])
                dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + 1);
            else
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
    }
    printf("%d\n", len - dp[len][len]);
}

 题目五：

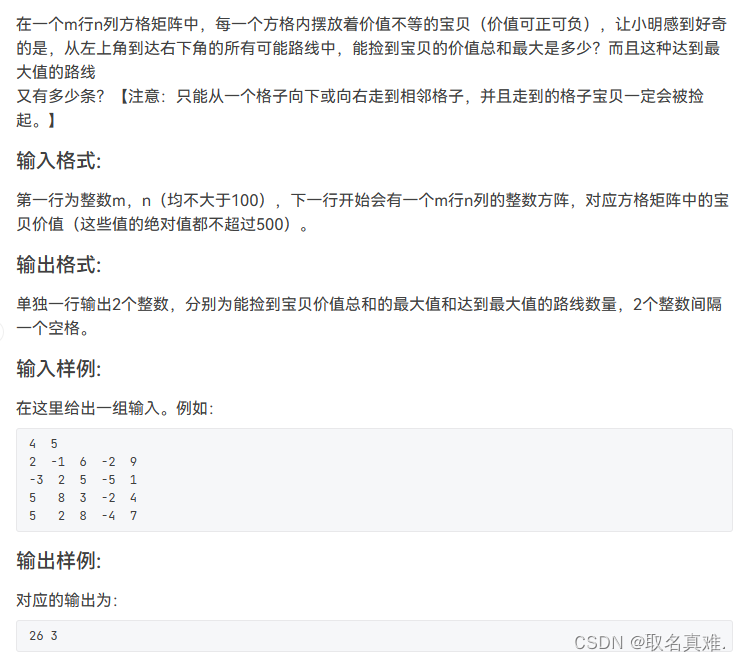
#include<iostream>
#include<cstring>
using namespace std;
struct node
{
    int w, step;
};
node dp[110][110];
int n, m, a[110][110];
int main()
{
    memset(dp, 0, sizeof(dp));
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
        {
            cin >> a[i][j];
        }
    for (int j = 1; j <= m; j++)//第一行
    {
        dp[1][j].w = dp[1][j - 1].w + a[1][j];
        dp[1][j].step = 1;
    }
    for (int i = 1; i <= n; i++)//第一列
    {
        dp[i][1].w = dp[i - 1][1].w + a[i][1];
        dp[i][1].step = 1;
    }
    for (int i = 2; i <= n; i++)
        for (int j = 2; j <= m; j++)
        {
            if (dp[i - 1][j].w > dp[i][j - 1].w)//上>左
            {
                dp[i][j].w = dp[i - 1][j].w + a[i][j];
                dp[i][j].step = dp[i - 1][j].step;
            }
            else if (dp[i - 1][j].w < dp[i][j - 1].w)//上<左
            {
                dp[i][j].w = dp[i][j - 1].w + a[i][j];
                dp[i][j].step = dp[i][j - 1].step;
            }
            else//相等时
            {
                dp[i][j].w = dp[i - 1][j].w + a[i][j];
                dp[i][j].step = dp[i][j - 1].step + dp[i - 1][j].step;//两个步数相加
            }
        }
    cout << dp[n][m].w << " " << dp[n][m].step << endl;
}

 题目六：

#include<iostream>
#include<cstring>
using namespace std;
int a[1010100], b[1010100],dp[1010100];
int n,tmp;
void prin(int k)
{
    if(k>n-3)//大于n-3 即可以直接跳到终点
    { cout<<k<<endl;return ;}
    else
        cout<<k<<" ";
    prin(b[k]);
}
int main()
{
	memset(a, 0, sizeof(a));
	cin >> n;
	for (int i = 0; i <= n; i++)
	{
		cin >> a[i];
	}
	for (int i = n - 3; i >= 0; i--)//从后往前走
	{
		tmp = a[i + 1];//从后一格来
		b[i] = i + 1;
		if (tmp > a[i + 2])//后两格
		{
			b[i] = i + 2;
			tmp = a[i + 2];
		}
		if (tmp > a[i + 3])//后三格
		{
			b[i] = i + 3;
			tmp = a[i + 3];
		}
		a[i] += tmp ;
	}
	cout << a[0] << endl;
    prin(0);
}

 题目七：

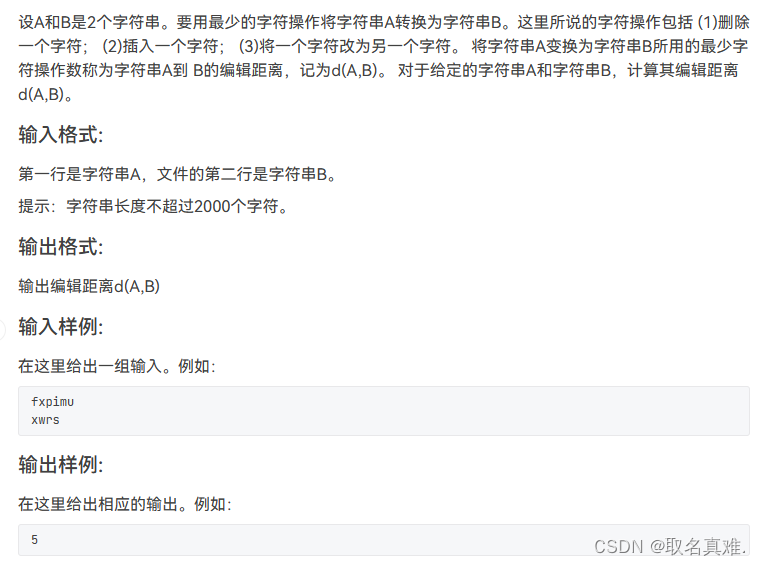
#include<iostream>//最长公共子序列
#include<cstring>
using namespace std;
int dp[2010][2010];
int main()
{
    string s1, s2;
    cin >> s1 >> s2;
    memset(dp, 0, sizeof(dp));
    int len1 = s1.size(), len2 = s2.size();
    for (int j = 1; j <= len2; j++)  
        dp[0][j] = dp[0][j - 1] + 1;
    for (int i = 1; i <= len1; i++)  
        dp[i][0] = dp[i - 1][0] + 1;
    for (int i = 1; i <= len1; i++)
    {
        for (int j = 1; j <= len2; j++)
        {
            if (s1[i - 1] == s2[j - 1])//两个字符相同，不做操作
                dp[i][j] = dp[i - 1][j - 1];
            else//不相同，选择三种操作中，操作数最小的
                dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
        }//dp[i-1][j-1]表示替换，dp[i-1][j]表示删除a[i]字符，dp[i][j-1]表示在a[i]后插入
    }
    cout << dp[len1][len2] << endl;
}

 题目八：

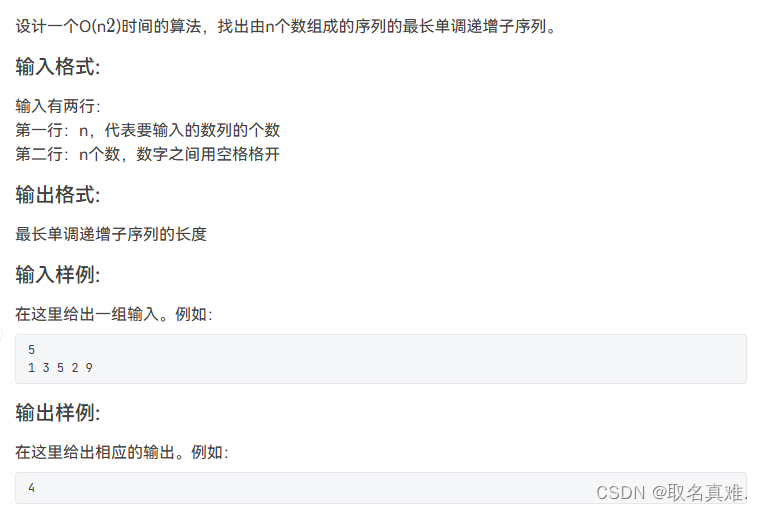
#include<iostream>
#include<cstring>
using namespace std;
int n;
int a[100100];
int f[100100];//以j结尾的最大递增序列
int ans = 0;
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
		f[i] = 1;//以i结尾的数的最大递增序列，起始都是包含自己的一个
	}
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= i; j++)//从a[1]到a[i]的循环
		{
			if (a[i] > a[j] && f[j]+1 > f[i])//第i个大于第j个且 以j结尾的最大递增序列加上一个（即a[i]这个数）大于 原先以i结尾的最大递增子序列
			{
				f[i] = f[j] + 1;
				ans = max(ans, f[i]);
			}
		}
	}
	cout << ans <<endl;
}

题目九：

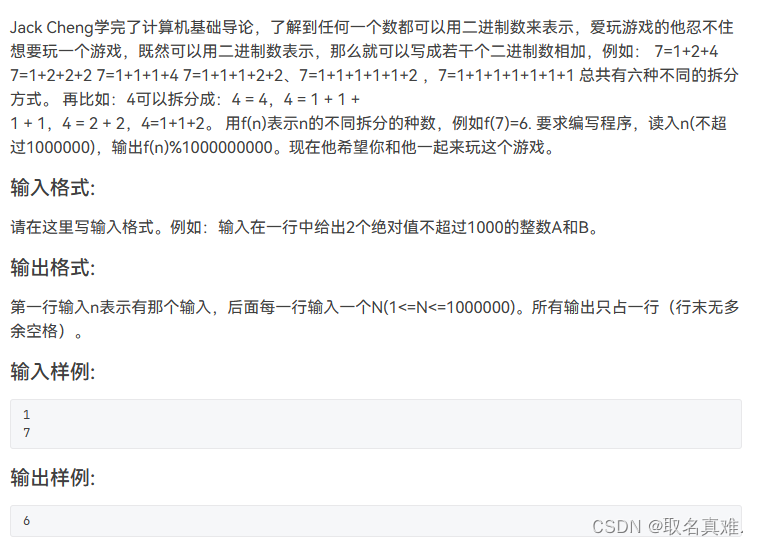
#include<iostream>//看成背包问题
using namespace std;
int v[21];
int dp[1000001];//表示装j有几种方法
int mod = 1e9;
int main() 
{
	int i, j, n, k;
    v[0]=1;
	for (i = 1; i <= 20; i++)//初始化体积
		v[i]=2*v[i-1];
	for (j = 0; j <= 1000000; j++) //每个j都至少有一种方法，全为1
		dp[j] = 1;
	for (i = 1; i <= 20; i++)//从第一件物品开始装，每件物品有无限个
		for (j = v[i]; j <= 1000000; j++)
				dp[j] = (dp[j] + dp[j - v[i]]) % mod;
    cin>>n;
	while (n--)
	{
		cin >> k;
		cout << dp[k];
		if (n != 0)
			cout << " ";
	}

}


http://www.kler.cn/a/272056.html

相关文章：

  • 如何给自己的域名配置免费的HTTPS How to configure free HTTPS for your domain name
  • Android系统开发（十五）：从 60Hz 到 120Hz，多刷新率进化简史
  • 简识JVM私有内存区域栈、数据结构
  • YOLOv5训练自己的数据及rknn部署
  • 博客搭建 — GitHub Pages 部署
  • 【FISCO BCOS】二十四、通过Java SDK对FISCO BCOS进行压力测试
  • 继承 ResponseEntityExceptionHandler
  • 2024云服务器安装MySQL，连接Navicat保姆级教程
  • Realtek PCIE Ethenter - PG Tool 使用操作說明
  • SpringBoot整合ElasticSearch应用
  • python中pdf转图片的操作方法二
  • “城市绿肺诊断：集成GIS、RS、VORS模型、CCDM模型、geodetecto、GWR模型技术深入解析生态系统与城镇化协调发展“
  • 接口幂等性问题和常见解决方案
  • LLM之RAG实战（二十九）| 探索RAG PDF解析
  • Flutter开发进阶之使用工具效率开发
  • 京东云主机+京美建站SaaS版
  • Python程序设计基础——代码习题
  • Python常见报错疑难杂症的解决思路解决方案
  • 【学习张天禹老师的vue课程发现的一个问题-vue销毁时候到底会不会解绑原生的dom事件？】
  • Halcon OCR文字识别
  • 【方法封装】时间格式化输出，获取请求设备和IP
  • 代码随想录算法训练营day24 | 回溯算法理论基础、77.组合
  • IIS上部署.netcore WebApi项目及swagger
  • Mysql 索引、锁与MVCC等相关知识点
  • webpack5零基础入门-10babel的使用
  • 第三篇 - 概述- IAB受众和技术标准 - IAB视频广告标准《数字视频和有线电视广告格式指南》