当前位置：首页 > article >正文

组合逻辑电路（四）

article 2025/1/20 21:48:05

目录

采用MSI的组合逻辑电路的分析与设计

采用MSI的组合逻辑电路的设计

用具有n个地址输入端的中规模集成器件实现n变量逻辑函数

用译码器设计组合逻辑电路

例

用数据选择器设计组合逻辑电路

例

用具有n个地址输入端的数据选择器实现m变量逻辑函数（m>n）

采用MSI的组合逻辑电路的分析

采用MSI的组合逻辑电路的分析与设计

采用MSI的组合逻辑电路的设计

中规模集成器件因具有体积、功能耗低、速度高及抗干扰能力强等一系列优点，得到了广泛的应用

在较复杂的数字逻辑电路设计中，以常用中规模集成器件和相应的功能电路为基本单元，取代门级组合电路，可以使设计过程大为简化，设计的电路工作更加可靠

另外也可以采用可编程逻辑器件设计

通常采用中规模集成电路设计组合逻辑电路可接一下步骤进行

根据题意列真值表

由真值表写逻辑函数表达式，将要实现的逻辑函数表达式变换成与所用中规模集成器件逻辑函数表达式相似的形式，比较两逻辑函数表达式（比较法）

逻辑函数比较可能出现下列几种情况：

若要实现的组合逻辑函数表达式与某种中规模集成器件的逻辑函数表达式形式上完全一致，则可选用该种器件实现设计

若要实现的组合逻辑函数表达式是某种中规模集成器件的逻辑函数表达式的一部分，则只需对器件多余的输入端作适当处理（接1或接0）即可

若要实现的组合逻辑函数的变量比某种中规模集成器件的输入变量多，则可通过扩展法或降维的方法来实现设计

根据比较结果，画出逻辑电路图

一般情况下，单输出的组合电路的逻辑函数选用器实现比较方便

而多输出的组合电路的逻辑函数选用译码器较好

对一些具有某些特点的逻辑函数，如逻辑函数输出为输入信号相加，则采用全加器实现较为方便

用具有n个地址输入端的中规模集成器件实现n变量逻辑函数

用译码器设计组合逻辑电路

由于n个输入变量的二进制译码器可提供2^n个最小项（或最小项的反函数）的输出，而任何一个逻辑函数都可变换为最小项之和的标准与-或表达式

因此，利用译码器和门电路可实现单输出和多输出组合逻辑电路

当译码器为输出低电平有效时，选用与非门

当译码器为输出高电平有效时，选用或门

例

试用3线-8线译码器74LS138和门电路实现下列多输出逻辑函数

$eq?F_%7B1%7D%3DA%5Cbar%7BC%7D+%5Cbar%7BA%7DBC+A%5Cbar%7BB%7DC$

$eq?F_%7B2%7D%3DA%5Cbar%7BB%7D%5Cbar%7BC%7D+%5Cbar%7BA%7D%5Cbar%7BB%7DC+BC$

$eq?F_%7B3%7D%3DA+%5Cbar%7BA%7DBC$

解

将F1~F3化为最小项之和形式，即

$eq?F_%7B1%7D%3DA%5Cbar%7BC%7D+%5Cbar%7BA%7DBC+A%5Cbar%7BB%7DC$

对于F1这个式子中有三项，一项中最多有3个变量，所以对于不同时存在三个变量的式子，通过 $eq?A+%5Cbar%7BA%7D%3D1$ ，进行变式，此式子中A与上面不同

F1中 $eq?A%5Cbar%7BC%7D$ ，不同时存在三个变量所以对 $eq?A%5Cbar%7BC%7D$ 进行变式

缺少变量B

$eq?A%5Cbar%7BC%7D%28%5Cbar%7BB%7D+B%29$

对于分配律有两种搭配

$eq?A%5Cbar%7BB%7D%5Cbar%7BC%7D+AB%5Cbar%7BC%7D$

即 $eq?F_%7B1%7D%3DA%5Cbar%7BB%7D%5Cbar%7BC%7D+AB%5Cbar%7BC%7D+%5Cbar%7BA%7DBC+A%5Cbar%7BB%7DC$

$eq?%3Dm_%7B4%7D+m_%7B6%7D+m_%7B3%7D+m_%7B5%7D$ $eq?A$

对于 $eq?A%5Cbar%7BB%7D%5Cbar%7BC%7D$ ，A不为非，B为非，C为非，所以对应100，二进制数对应的十进制数为4，所以m的下标为4

对于 $eq?AB%5Cbar%7BC%7D$ ，A不为非，B不为非，C为非，所以对应110，二进制数对应的十进制数为6，所以m的下标为6

对于 $eq?%5Cbar%7BA%7DBC$ ，A为非，B不为非，C不为非，所以对应011，二进制数对应的十进制数为3，所以m的下标为3

对于 $eq?A%5Cbar%7BB%7DC$ ，A不为非，B为非，C不为非，所以对应101，二进制数对应的十进制数为5，所以m的下标为5

所以F1的最小项之和形式为

$eq?F_%7B1%7D%3Dm_%7B3%7D+m_%7B4%7D+m_%7B5%7D+m_%7B6%7D$

$eq?F_%7B2%7D%3DA%5Cbar%7BB%7D%5Cbar%7BC%7D+%5Cbar%7BA%7D%5Cbar%7BB%7DC+BC$
对于F2这个式子中有三项，一项中最多有3个变量，所以对于不同时存在三个变量的式子，通过 $eq?A+%5Cbar%7BA%7D%3D1$ ，进行变式，此式子中A与上面不同

F2中 $eq?BC$ ，不同时存在三个变量所以对 $eq?BC$ 进行变式

缺少变量A

$eq?%28A+%5Cbar%7BA%7D%29BC$

对于分配律有两种搭配

$eq?ABC+%5Cbar%7BA%7DBC$

即 $eq?F_%7B2%7D%3DA%5Cbar%7BB%7D%5Cbar%7BC%7D+%5Cbar%7BA%7D%5Cbar%7BB%7DC+ABC+%5Cbar%7BA%7DBC$

$eq?%3Dm_%7B4%7D+m_%7B1%7D+m_%7B7%7D+m_%7B3%7D$

对于 $eq?A%5Cbar%7BB%7D%5Cbar%7BC%7D$ ，A不为非，B为非，C为非，所以对应100，二进制数对应的十进制数为4，所以m的下标为4

对于 $eq?%5Cbar%7BA%7D%5Cbar%7BB%7DC$ ，A为非，B为非，C不为非，所以对应001，二进制数对应的十进制数为1，所以m的下标为1

对于 $eq?ABC$ ，A不为非，B不为非，C不为非，所以对应111，二进制数对应的十进制数为7，所以m的下标为7

对于 $eq?%5Cbar%7BA%7DBC$ ，A为非，B不为非，C不为非，所以对应011，二进制数对应的十进制数为3，所以m的下标为3

所以F2的最小项之和形式为

$eq?F_%7B2%7D%3Dm_%7B1%7D+m_%7B3%7D+m_%7B4%7D+m_%7B7%7D$

$eq?F_%7B3%7D%3DA+%5Cbar%7BA%7DBC$

对于F3这个式子中有两项，一项中最多有3个变量，所以对于不同时存在三个变量的式子，通过 $eq?A+%5Cbar%7BA%7D%3D1$ ，进行变式，此式子中A与上面不同

F3中 $eq?A$ ，不同时存在三个变量所以对 $eq?A$ 进行变式

缺少变量B和C

$eq?A%28B+%5Cbar%7BB%7D%29%28C+%5Cbar%7BC%7D%29$

对于分配律有四种搭配

$eq?ABC+AB%5Cbar%7BC%7D+A%5Cbar%7BB%7DC+A%5Cbar%7BB%7D%5Cbar%7BC%7D$

即 $eq?F_%7B3%7D%3DABC+AB%5Cbar%7BC%7D+A%5Cbar%7BB%7DC+A%5Cbar%7BB%7D%5Cbar%7BC%7D+%5Cbar%7BA%7DBC$

$eq?%3Dm_%7B7%7D+m_%7B6%7D+m_%7B5%7D+m_%7B4%7D+m_%7B3%7D$

对于 $eq?ABC$ ，A不为非，B不为非，C不为非，所以对应111，二进制数对应的十进制数为7，所以m的下标为7

对于 $eq?AB%5Cbar%7BC%7D$ ，A不为非，B不为非，C为非，所以对应110，二进制数对应的十进制数为6，所以m的下标为6

对于 $eq?A%5Cbar%7BB%7DC$ ，A不为非，B为非，C不为非，所以对应101，二进制数对应的十进制数为5，所以m的下标为5

对于 $eq?A%5Cbar%7BB%7D%5Cbar%7BC%7D$ ，A不为非，B为非，C为非，所以对应100，二进制数对应的十进制数为4，所以m的下标为4

对于 $eq?%5Cbar%7BA%7DBC$ ，A为非，B不为非，C不为非，所以对应011，二进制数对应的十进制数为3，所以m的下标为3

$eq?F_%7B3%7D%3Dm_%7B3%7D+m_%7B4%7D+m_%7B5%7D+m_%7B6%7D+m_%7B7%7D$

令A2=A，A1=B，A0=C，将m0~m7用译码器输出 $eq?%5Cbar%7BY_%7Bi%7D%7D$ 表示，因此有

$eq?F_%7B1%7D%3D%5Coverline%7B%5Cbar%7Bm_%7B3%7D%7D%5Cbar%7Bm_%7B4%7D%7D%5Cbar%7Bm_%7B5%7D%7D%5Cbar%7Bm_%7B6%7D%7D%7D%3D%5Coverline%7B%5Cbar%7BY_%7B3%7D%7D%5Cbar%7BY_%7B4%7D%7D%5Cbar%7BY_%7B5%7D%7D%5Cbar%7BY_%7B6%7D%7D%7D$

$eq?F_%7B2%7D%3D%5Coverline%7B%5Cbar%7Bm_%7B1%7D%7D%5Cbar%7Bm_%7B3%7D%7D%5Cbar%7Bm_%7B4%7D%7D%5Cbar%7Bm_%7B7%7D%7D%7D%3D%5Coverline%7B%5Cbar%7BY_%7B1%7D%7D%5Cbar%7BY_%7B3%7D%7D%5Cbar%7BY_%7B4%7D%7D%5Cbar%7BY_%7B7%7D%7D%7D$

$eq?F_%7B3%7D%3D%5Coverline%7B%5Cbar%7Bm_%7B3%7D%7D%5Cbar%7Bm_%7B4%7D%7D%5Cbar%7Bm_%7B5%7D%7D%5Cbar%7Bm_%7B6%7D%7D%5Cbar%7Bm_%7B7%7D%7D%7D%3D%5Coverline%7B%5Cbar%7BY_%7B3%7D%7D%5Cbar%7BY_%7B4%7D%7D%5Cbar%7BY_%7B5%7D%7D%5Cbar%7BY_%7B6%7D%7D%5Cbar%7BY_%7B7%7D%7D%7D$

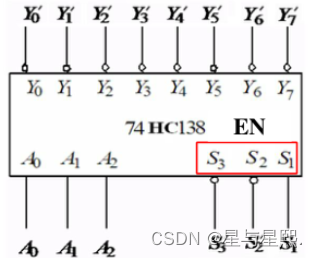
3线-8线译码器：

根据式子可画出F1~F3的逻辑电路

即

输出变量Y3Y4Y5Y6同时取与非后输出F1

输出变量Y1Y3Y4Y7同时取与非后输出F2

输出变量Y3Y4Y5Y6Y7同时取与非后输出F3

用数据选择器设计组合逻辑电路

由于数据选择器在输入全部数据都为1时，输出为输入地址变量全部最小项的和，而任一逻辑函数都可变换为最小项之和的标准与或表达式

如数据选择器的输入数据 $eq?D_%7Bi%7D%3D1$ ，则在数据选择器输出逻辑函数表达式中，相应最小项保留

如数据 $eq?D_%7Bi%7D%3D0$ ，则相应最小项就不存在

这里i=0.1，2，...，n-1

利用数据选择器的这一特点，可以方便地实现组合逻辑函数

例

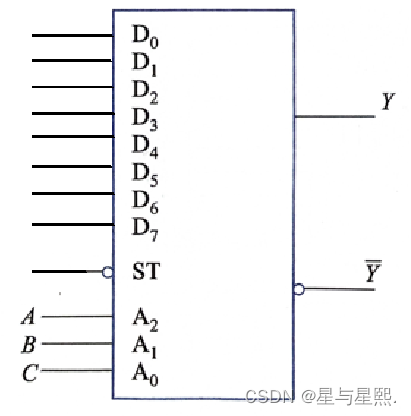
试用数据选择器74LS151实现下列逻辑函数

$eq?F%3D%5Cbar%7BA%7DB+%5Coverline%7BA%5Cbigoplus%20C%7D$

解

由于要实现的逻辑函数有3个变量，而8选1数据选择器74LS151有3位地址码，所以只要将这3个变量和3位地址码对应相连便可直接利用该数据选择器实现逻辑函数

该题可用卡诺图法和代数法求解

卡诺图法：

写出逻辑函数F的标准与或表达式为

$eq?F%3D%5Cbar%7BA%7DB+%5Coverline%7BA%5Cbigoplus%20C%7D$ $eq?%5Coverline%7BA%5Cbar%7BC%7D+%5Cbar%7BA%7DC%7D%3D%5Coverline%7BA%5Cbigoplus%20C%7D%3DA%5Cbigodot%20C%3DAC+%5Cbar%7BA%7D%5Cbar%7BC%7D$

$eq?%3D%5Cbar%7BA%7DB+A%5Cbar%7BC%7D+%5Cbar%7BA%7DC$

对于F这个式子中有三项，一项中最多有3个变量，所以对于不同时存在三个变量的式子，通过 $eq?A+%5Cbar%7BA%7D%3D1$ ，进行变式，此式子中A与上面不同

F中 $eq?%5Cbar%7BA%7DB$ 、 $eq?AC$ 和 $eq?%5Cbar%7BA%7D%5Cbar%7BC%7D$ ，不同时存在三个变量所以对 $eq?%5Cbar%7BA%7DB$ 、 $eq?AC$ 和 $eq?%5Cbar%7BA%7D%5Cbar%7BC%7D$ 进行变式

对于 $eq?%5Cbar%7BA%7DB$

$eq?%5Cbar%7BA%7DB%28C+%5Cbar%7BC%7D%29$

对于分配律有两种搭配

$eq?%5Cbar%7BA%7DBC+%5Cbar%7BA%7DB%5Cbar%7BC%7D$

对于 $eq?AC$

$eq?AC%28B+%5Cbar%7BB%7D%29$

对于分配律有两种搭配

$eq?ABC+A%5Cbar%7BB%7DC$

对于 $eq?%5Cbar%7BA%7D%5Cbar%7BC%7D$

$eq?%5Cbar%7BA%7D%5Cbar%7BC%7D%28B+%5Cbar%7BB%7D%29$

对于分配律有两种搭配

$eq?%5Cbar%7BA%7DB%5Cbar%7BC%7D+%5Cbar%7BA%7D%5Cbar%7BB%7D%5Cbar%7BC%7D$

即 $eq?F%3D%5Cbar%7BA%7DBC+%5Cbar%7BA%7DB%5Cbar%7BC%7D+ABC+A%5Cbar%7BB%7DC+%5Cbar%7BA%7DB%5Cbar%7BC%7D+%5Cbar%7BA%7D%5Cbar%7BB%7D%5Cbar%7BC%7D$

$eq?%5Cbar%7BA%7DBC+%5Cbar%7BA%7DB%5Cbar%7BC%7D+ABC+A%5Cbar%7BB%7DC+%5Cbar%7BA%7D%5Cbar%7BB%7D%5Cbar%7BC%7D$ 利用公式 $eq?A+A%3DA$ 将相应项合并

$eq?%3Dm_%7B3%7D+m_%7B2%7D+m_%7B7%7D+m_%7B5%7D+m_%7B0%7D$

对于 $eq?%5Cbar%7BA%7DBC$ ，A为非，B不为非，C不为非，所以对应011，二进制数对应的十进制数为3，所以m的下标为3

对于 $eq?%5Cbar%7BA%7DB%5Cbar%7BC%7D$ ，A为非，B不为非，C为非，所以对应010，二进制数对应的十进制数为2，所以m的下标为2

对于 $eq?ABC$ ，A不为非，B不为非，C不为非，所以对应111，二进制数对应的十进制数为7，所以m的下标为7

对于 $eq?A%5Cbar%7BB%7DC$ ，A不为非，B为非，C不为非，所以对应101，二进制数对应的十进制数为5，所以m的下标为5

对于 $eq?%5Cbar%7BA%7D%5Cbar%7BB%7D%5Cbar%7BC%7D$ ，A为非，B为非，C为非，所以对应000，二进制数对应的十进制数为0，所以m的下标为0

$eq?F%3Dm_%7B0%7D+m_%7B2%7D+m_%7B3%7D+m_%7B5%7D+m_%7B7%7D$

写出CC74HCT151的输出逻辑函数Y的表达式， $eq?%5Coverline%7BST%7D%3D0$ 时

$eq?Y%3D%5Cbar%7BA_%7B2%7D%7D%5Cbar%7BA_%7B1%7D%7D%5Cbar%7BA_%7B0%7D%7DD_%7B0%7D+%5Cbar%7BA_%7B2%7D%7D%5Cbar%7BA_%7B1%7D%7DA_%7B0%7DD_%7B1%7D+%5Cbar%7BA_%7B2%7D%7DA_%7B1%7D%5Cbar%7BA_%7B0%7D%7DD_%7B2%7D+%5Cbar%7BA_%7B2%7D%7DA_%7B1%7DA_%7B0%7DD_%7B3%7D+A_%7B2%7D%5Cbar%7BA_%7B1%7D%7D%5Cbar%7BA_%7B0%7D%7DD_%7B4%7D+A_%7B2%7D%5Cbar%7BA_%7B1%7D%7DA_%7B0%7DD_%7B5%7D+A_%7B2%7DA_%7B1%7D%5Cbar%7BA_%7B0%7D%7DD_%7B6%7D+A_%7B2%7DA_%7B1%7DA_%7B0%7DD_%7B7%7D$

$eq?%3Dm_%7B0%7DD_%7B0%7D+m_%7B1%7DD_%7B1%7D+m_%7B2%7DD_%7B2%7D+m_%7B3%7DD_%7B3%7D+m_%7B4%7DD_%7B4%7D+m_%7B5%7DD_%7B5%7D+m_%7B6%7DD_%7B6%7D+m_%7B7%7DD_%7B7%7D$

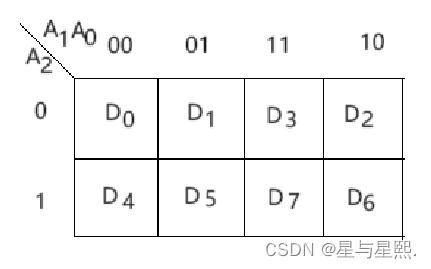
画出F和Y的卡诺图
令A=A2、B=A1、C=A0，比较F和Y两个卡诺图可得

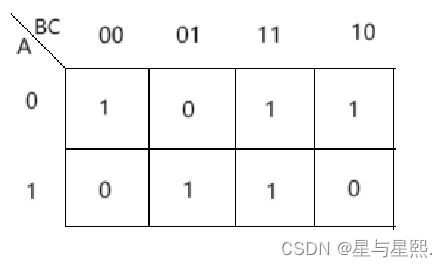
D1=D4=D6=0

D0=D2=D3=D5=D7=1

代数法：

写出逻辑函数F的最小项表达式为

$eq?F%3D%5Cbar%7BA%7DB+%5Coverline%7BA%5Cbigoplus%20C%7D$

由上可知

$eq?F%3Dm_%7B0%7D+m_%7B2%7D+m_%7B3%7D+m_%7B5%7D+m_%7B7%7D$

写出CC74HCT151输出逻辑函数Y的表达式为

$eq?Y%3D%5Cbar%7BA_%7B2%7D%7D%5Cbar%7BA_%7B1%7D%7D%5Cbar%7BA_%7B0%7D%7DD_%7B0%7D+%5Cbar%7BA_%7B2%7D%7D%5Cbar%7BA_%7B1%7D%7DA_%7B0%7DD_%7B1%7D+%5Cbar%7BA_%7B2%7D%7DA_%7B1%7D%5Cbar%7BA_%7B0%7D%7DD_%7B2%7D+%5Cbar%7BA_%7B2%7D%7DA_%7B1%7DA_%7B0%7DD_%7B3%7D+A_%7B2%7D%5Cbar%7BA_%7B1%7D%7D%5Cbar%7BA_%7B0%7D%7DD_%7B4%7D+A_%7B2%7D%5Cbar%7BA_%7B1%7D%7DA_%7B0%7DD_%7B5%7D+A_%7B2%7DA_%7B1%7D%5Cbar%7BA_%7B0%7D%7DD_%7B6%7D+A_%7B2%7DA_%7B1%7DA_%7B0%7DD_%7B7%7D$

$eq?%3Dm_%7B0%7DD_%7B0%7D+m_%7B1%7DD_%7B1%7D+m_%7B2%7DD_%7B2%7D+m_%7B3%7DD_%7B3%7D+m_%7B4%7DD_%7B4%7D+m_%7B5%7DD_%7B5%7D+m_%7B6%7DD_%7B6%7D+m_%7B7%7DD_%7B7%7D$

比较F和Y两式中对应最小项的关系

设A=A2、B=A1，C=A0，且F=Y

比较F和Y两式中的最小项，若F式中的最小项为mi，则Y式中对应mi最小项的数据Di=1，若F式中没有的最小项为mj，则Y式中对应mj最小项的数据Dj=0，由此可得

D1=D4=D6=0

D0=D2=D3=D5=D7=1

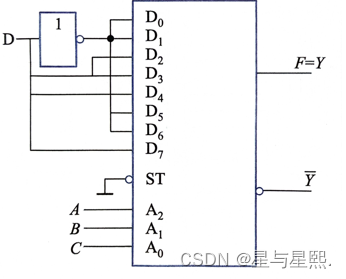
根据上式画出逻辑图与图

用具有n个地址输入端的数据选择器实现m变量逻辑函数（m>n）

用两片n个地址输入端的数据选择器实现m变量逻辑函数（扩展法）

用具有n个地址输入端的数据选择器实现变量m的逻辑函数（代数法）

用具有n个地址输入端的数据选择器实现m变量逻辑函数（降维图）

采用MSI的组合逻辑电路的分析

以中规模集成电路为核心构成的组合逻辑电路的分析方法，与用小规模集成电路构成的组合电路的分析方法有不同之处

中规模集成电路的多样性和复杂性，给组合电路的分析带来一定的困难

分析过程与结果是否正确，取决于分析者对常用功能电路的熟悉程度和经验

基本分析步骤如下：

对给定的逻辑电路图加以分析，根据电路的复杂程度和器件类型，将电路划分为一个或多个逻辑功能块

写出功能块的逻辑函数表达式

由逻辑函数式列真值表

根据逻辑函数表达式或真值表分析出功能块的逻辑功能

如果有多个逻辑功能块，则在各功能块电路分析的基础上，对整个电路进行整体功能的分析