算法——贪心
「贪心的本质是选择每一阶段的局部最优,从而达到全局最优」
贪心无套路
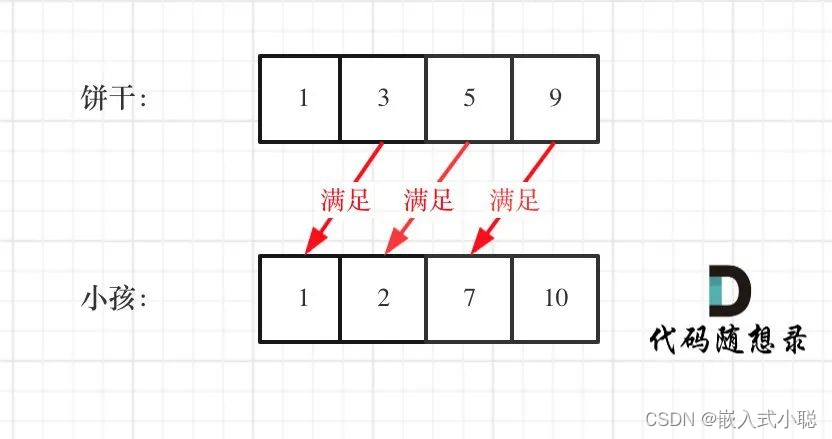
1. 分发饼干
贪心策略:
(1)局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩
(2)局部最优就是小饼干喂给胃口小的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩
代码实现:
// 冒泡排序 void sort(int *a, int len) { int flag = 1; for (int i = len - 1; flag && i > 0; i--) { flag = 0; for (int j = 0; j < i; j++) { if (a[j] > a[j + 1]) { flag = 1; int temp = a[j]; a[j] = a[j + 1]; a[j + 1] = temp; } } } } int findContentChildren(int *g, int gSize, int *s, int sSize) { sort(g, gSize); sort(s, sSize); int j = 0; int sum = 0; for (int i = 0; i < gSize; i++) { while (j < sSize && s[j] < g[i]) { j++; } if (j < sSize) { sum++; j++; } } return sum; }
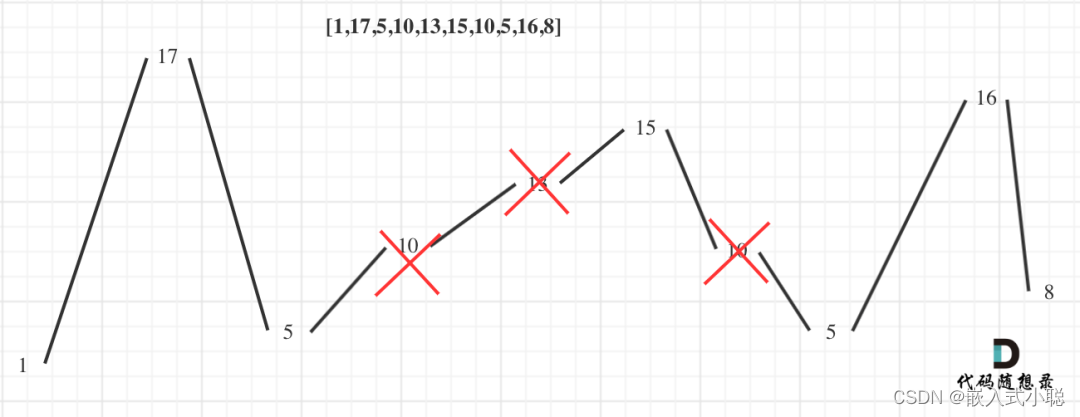
2. 摆动序列
贪心策略:
「局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值」
「整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列」
「实际操作上,其实连删除的操作都不用做,因为题目要求的是最长摆动子序列的长度,所以只需要统计数组的峰值数量就可以了(相当于是删除单一坡度上的节点,然后统计长度)」
代码实现:
int wiggleMaxLength(int *nums, int numsSize) { if (numsSize <= 1) { return numsSize; } int now = 0; // 当前一对峰值 int pre = 0; // 前一对峰值 int result = 1; // 记录峰值个数,序列默认序列最右边有一个峰值 for (int i = 1; i < numsSize; i++) { now = nums[i] - nums[i - 1]; // 出现峰值 if ((now > 0 && pre <= 0) || (pre >= 0 && now < 0)) { result++; pre = now; } } return result; }
3. 最大子数组和
暴力解法:超时
int maxSubArray(int *nums, int numsSize) { int result = INT32_MIN; int count = 0; for (int i = 0; i < numsSize; i++) { // 设置起始位置 count = 0; for (int j = i; j < numsSize; j++) { // 每次从起始位置i开始遍历寻找最大值 count += nums[j]; result = count > result ? count : result; } } return result; }动规五步曲:
确定dp数组(dp table)以及下标的含义
dp[i]:以 i 结尾的最大连续子序列和为dp[i]
确定递推公式(容斥原理)
dp[i]只有两个方向可以推出来:
dp[i - 1] + nums[i],即:nums[i]加入当前连续子序列和
nums[i],即:从头开始计算当前连续子序列和
一定是取最大的,所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);
#define max(a, b) ((a) > (b) ? (a) : (b)) int maxSubArray(int *nums, int numsSize) { if (numsSize == 0) { // 特殊情况 return 0; } int dp[numsSize]; dp[0] = nums[0]; int result = dp[0]; for (int i = 1; i < numsSize; i++) { dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移方程 result = max(result, dp[i]); // result 保存dp[i]的最大值 } return result; }贪心策略:
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小
全局最优:选取最大“连续和”
int maxSubArray(int *nums, int numsSize) { int result = INT32_MIN; int count = 0; for (int i = 0; i < numsSize; i++) { count += nums[i]; if (count > result) { // 取区间累计的最大值(相当于不断确定最大子序终止位置) result = count; } if (count <= 0) { count = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和 } } return result; }
4. 买卖股票的最佳时机||
贪心策略:
「局部最优:收集每天的正利润,全局最优:求得最大利润」
5. 跳跃游戏
贪心策略:
「贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点」
6. 跳跃游戏||
7. K次取反后最大化的数组和
贪心策略:
局部最优:让绝对值大的负数变为正数,当前数值达到最大,整体最优:整个数组和达到最大
如果将负数都转变为正数了,K依然大于0
局部最优:只找数值最小的正整数进行反转,当前数值可以达到最大,全局最优:整个 数组和 达到最大
第一步:将数组按照绝对值大小从大到小排序,「注意要按照绝对值的大小」
第二步:从前向后遍历,遇到负数将其变为正数,同时K--
第三步:如果K还大于0,那么反复转变数值最小的元素,将K用完
第四步:求和
8. 加油站