leetcode 3080
leetcode 3080
题目

例子

思路
创建数组,记录nums 的值 对应的id, 按照大小排序。
代码实现
class Solution {
public:
vector<long long> unmarkedSumArray(vector<int>& nums, vector<vector<int>>& queries) {
vector<long long> res;
int n = nums.size();
/*
ids 数组是为了记录nums的val的index的序列。
举个例子:
nums = [1,2,2,1,2,3,1]
ids[0] [1] [2] 对应的值是0, 3, 6
因为nums[0], nums[3], nums[6] 的值都是1,是最小值;
*/
vector<int> ids(n);
iota(ids.begin(), ids.end(), 0);
ranges::stable_sort(ids, [&](int i, int j) { return nums[i] < nums[j]; });
for(int i=0; i<queries.size(); i++){
int q_id = queries[i][0];
int q_num = queries[i][1];
// 被标记的id 的nums的值,设置为0, 这样计算sum 的时候,直接默认标记了。
// 已知nums 是正整数数组,正整数的范围是 >0 的。
nums[q_id] = 0;
int j =0;
while(q_num > 0 && j<n){
int num_id = ids[j];
if(nums[num_id] == 0){
j++;
}else{
nums[num_id] = 0;
q_num--;
j++;
}
}
long long sum = std::accumulate(nums.begin(), nums.end(), 0);
res.push_back(sum);
}
return res;
}
};
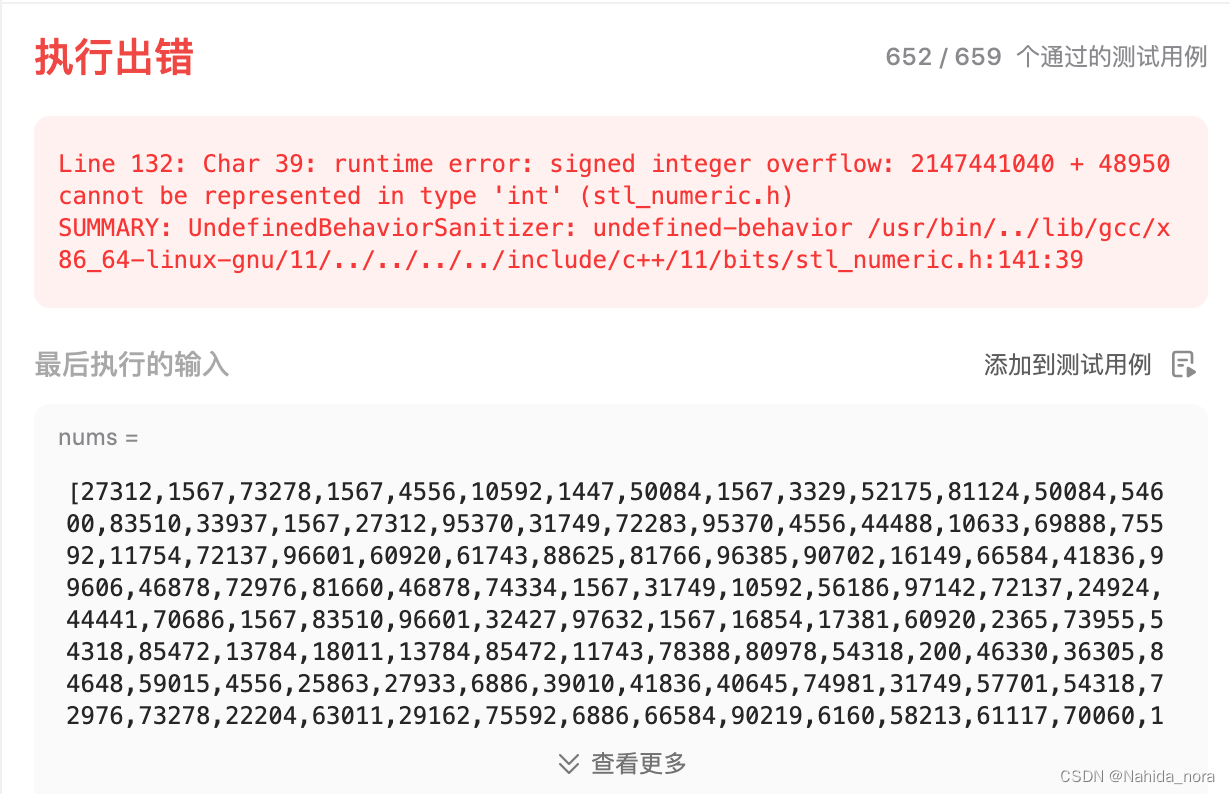
long long sum = std::accumulate(nums.begin(), nums.end(), 0LL);
解决了runtime error , 还是有超时问题。

class Solution {
public:
vector<long long> unmarkedSumArray(vector<int>& nums, vector<vector<int>>& queries) {
vector<long long> res;
int n = nums.size();
long long sum = std::accumulate(nums.begin(), nums.end(), 0LL);
/*
ids 数组是为了记录nums的val的index的序列。
举个例子:
nums = [1,2,2,1,2,3,1]
ids[0] [1] [2] 对应的值是0, 3, 6
因为nums[0], nums[3], nums[6] 的值都是1,是最小值;
*/
vector<int> ids(n);
iota(ids.begin(), ids.end(), 0);
ranges::stable_sort(ids, [&](int i, int j) { return nums[i] < nums[j]; });
int j =0;
for(int i=0; i<queries.size(); i++){
int q_id = queries[i][0];
int q_num = queries[i][1];
// 被标记的id 的nums的值,设置为0, 这样计算sum 的时候,直接默认标记了。
// 已知nums 是正整数数组,正整数的范围是 >0 的。
sum = sum - nums[q_id];
nums[q_id] = 0;
while(q_num > 0 && j<n){
int num_id = ids[j];
if(nums[num_id] > 0){
sum = sum - nums[num_id];
nums[num_id] = 0;
q_num--;
}
j++;
}
res.push_back(sum);
}
return res;
}
};
减少while or loop 里的计算or 判断,可以减少执行时间。
分析
时间复杂度:
O(nlogn)
stable_sort 的时间复杂度是nlogn;
stable_sort 使用的是归并排序;
对于递归方程 T(n) = 2T(n/2) + O(n),我们可以通过分析归并排序的算法流程来推导出时间复杂度为 O(n log n)。
- 根据递归方程 T(n) = 2T(n/2) + O(n),我们可以得到以下递归树:
T(n)
/ \
T(n/2) T(n/2)
/ \ / \
T(n/4) T(n/4) T(n/4) T(n/4)
-
递归树的每一层的时间复杂度为 O(n),因为每层的合并操作需要线性时间。
-
递归树的高度为 log n,因为每次将序列一分为二,直到子序列只有一个元素。
-
在递归树的每一层,都有 O(n) 的合并操作,总共有 log n 层,因此总的时间复杂度为 O(n log n)。
综上所述,通过对递归方程和递归树的分析,可以得出归并排序的时间复杂度为 O(n log n)。
希望这个解释能够帮助您理解如何从递归方程推导出时间复杂度为 O(n log n)。如果您有任何其他问题,请随时告诉我。
空间复杂度:
O(n)
stable_sort 函数
对于 ranges::stable_sort(ids, [&](int i, int j) { return nums[i] < nums[j]; }); 这样的调用方式,我们可以简单地了解其实现原理。由于 ranges::stable_sort 是 C++20 中引入的新函数,其具体实现可能会因标准库的不同而有所差异。以下是一个简单的伪代码示例,展示了 ranges::stable_sort 的可能实现:
template <class RandomAccessIterator, class Compare>
void ranges::stable_sort(RandomAccessIterator first, RandomAccessIterator last, Compare comp) {
if (first == last) return;
using value_type = typename std::iterator_traits<RandomAccessIterator>::value_type;
std::vector<value_type> temp(first, last); // 将范围内的元素复制到临时数组中
// 使用 lambda 表达式作为比较函数
auto lambda_comp = [&](int i, int j) { return comp(temp[i], temp[j]); };
std::stable_sort(temp.begin(), temp.end(), lambda_comp); // 使用 std::stable_sort 对临时数组进行排序
std::copy(temp.begin(), temp.end(), first); // 将排序后的元素复制回原始范围
}
上述伪代码简单地描述了 ranges::stable_sort 的实现思路。首先,将范围内的元素复制到临时数组中,然后使用 lambda 表达式作为比较函数,对临时数组进行排序,最后将排序后的元素复制回原始范围。这种实现方式保证了稳定排序的特性。
需要注意的是,实际的 ranges::stable_sort 实现可能会更加复杂,因为它需要考虑范围操作、迭代器特性、元素类型等多个因素。
accumulate 函数
std::accumulate 是 C++ 标准库中的一个算法函数,用于对一个范围内的元素进行累积操作。它定义在 <numeric> 头文件中。
std::accumulate 函数的原型如下:
template< class InputIt, class T >
T accumulate( InputIt first, InputIt last, T init );
其中:
InputIt是输入迭代器的类型,用于指定范围的开始和结束位置。T是累积结果的类型,也是初始值的类型。first和last分别是指向范围的起始和结束位置的迭代器。init是初始值,用于初始化累积结果。
std::accumulate 函数会从 first 到 last 遍历范围内的元素,对它们进行累积操作。具体而言,它将初始值 init 和范围内的每个元素进行二元操作(通常是加法),并将结果存储在累积结果中。最终返回累积结果。
以下是一个示例用法:
#include <iostream>
#include <vector>
#include <numeric>
int main() {
std::vector<int> vec = {1, 2, 3, 4, 5};
// 使用 std::accumulate 函数计算和
int sum = std::accumulate(vec.begin(), vec.end(), 0);
std::cout << "Sum of elements in the vector: " << sum << std::endl;
return 0;
}
在这个示例中,我们使用 std::accumulate 函数计算了一个 std::vector 中所有元素的和,并将结果打印到控制台上。
std::accumulate 函数在处理累积操作时非常方便,可以用于对容器中的元素进行求和、求积、计算平均值等操作。希望这个介绍能够帮助您理解 std::accumulate 函数的用法。如果您有任何其他问题,请随时告诉我。
