学完排序算法，终于知道用什么方法给监考完收上来的试卷排序……

由于每个老师批改完卷子之后装袋不一定是有序的，鼠鼠我被拉去当给试卷排序的苦力。面对堆积成山的试卷袋，每一份试卷袋的试卷集又很重，鼠鼠我啊为了尽早下班，决定用一种良好的办法进行排序。

1.插入排序

首先考虑的是插入排序。第一份试卷就当做已经有序了；第二份试卷序号如果比第一份试卷小，那么放在第一份试卷的上面，否则放在下面；第三份试卷又放在前两份试卷集合的正确位置。总之，保证我拿到一份试卷，这一份试卷就插入到了正确的位置。

这一个排序算法看起来是生活中用的最常见的（因为看上去其他苦力鼠鼠也是这么干的），代码也是比较好写的：i迭代完1次说明1个元素有了相对排好序的位置。注意，第一次我们跳过了i=0，实际上默认第一个就是相对有序的（本来它就只有一个，所以有序）。i = 1，说明我们正在给i=1的试卷进行插入操作，而前面如果排好序的元素大于它，就一个一个往后移，直到找到一个学号小于当前我们拿到的试卷上填的学号，我们就放在这个试卷的后面。

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        for(int i = 1; i < nums.size(); ++i){//从第二个开始排
            int key = nums[i];
            int j = i - 1;
            while(j >= 0 && nums[j] > key){
                nums[j + 1] = nums[j];
                j = j - 1;
            }
            nums[j + 1] = key;

        }
        return nums;
    }
};

再来一个注释版本，跟上面是一样的

#include <vector>
using namespace std;

class Solution {
public:
    void insertionSort(vector<int>& nums) {
        int n = nums.size();
        for (int i = 1; i < n; i++) {
            int key = nums[i]; // 取出未排序部分的第一个元素
            int j = i - 1;

            // 将大于key的元素向后移动一个位置
            while (j >= 0 && nums[j] > key) {
                nums[j + 1] = nums[j];
                j = j - 1;
            }
            nums[j + 1] = key; // 找到了key的正确位置，插入key
        }
    }

    vector<int> sortArray(vector<int>& nums) {
        insertionSort(nums);
        return nums;
    }
};

2. 改良：归并+插入排序

但是试卷实在太重了，一个班有60个人，每个人有2页试卷，2页答题纸，2页草稿纸……排序到后面，鼠鼠真的没有力气捧着排好序的试卷挨个插入。

于是聪明的鼠鼠想了一个办法：把试卷分成两叠（或者更多叠，看试卷一共有多少份）。两叠内用插入排序，那么能够得到两叠排好序的试卷，这样鼠鼠每次捧在手上的试卷少了，插入排序也排的很轻松（知识点：插入排序对小数据集非常高效）。

而针对两叠有序的试卷，就可以进行归并排序了。注意，这只是归并排序中两块merge的部分操作，而省去了归并排序中递归拆分到大小为1然后再两两merge的操作。简单来说，这里使用到了归并排序的最后一步，在我参考的博客中找了个图如下，用到的是红框中标出的排序理念：

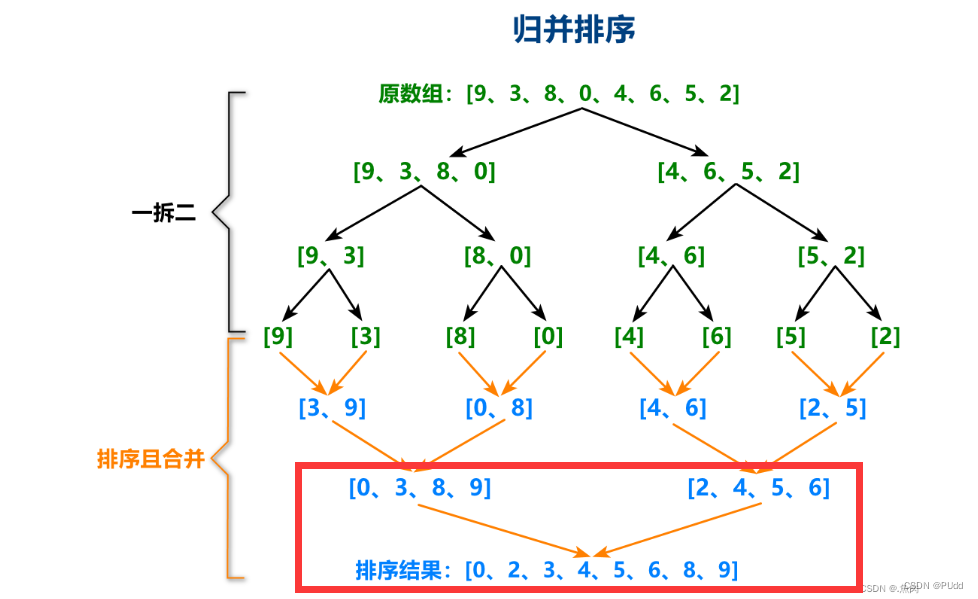
此时，我们其实是双指针分别指着两堆试卷的头，哪个序号小就放在temp数组里面，最后我们的temp数组就存放了所有的排好序的试卷（真是伟大的鼠鼠，聪明的鼠鼠！）如果一个班的同学更多一点，那么我们实际上可以将其分成四份，合并过程则为该图的后三行。1、2两个数组先合并，3、4两个数组先合并，最后剩下来的两个数组继续合并。

归并排序算法如下：

代码思路也很简单，主要是用到的递归。第一个merge块其实就是做了我刚刚给两坨有序试卷双指针飞快排序的过程；而第二个merge_recursive实际上是做了图上第一块讲的“一拆二”的过程，拆到每份试卷只剩一个，再进行merge。

class Solution {
public:
    void merge(int left,  int mid, int right,vector<int>& nums, vector<int>& temp){
        int i = left;
        int j = mid + 1;
        int k = 0;
        while(i <= mid && j <= right){
            if(nums[i] <= nums[j])
                temp[k++] = nums[i++];
            else temp[k++] = nums[j++];
        }
        while(i <= mid){
            temp[k++] = nums[i++];
        }
        while(j <= right){
            temp[k++] = nums[j++];
        }

        for (i = left, k = 0; i <= right; i++, k++) {
            nums[i] = temp[k];
        }
    }

    void merge_recursive(int left, int right, vector<int>&nums, vector<int>& temp){
        if(left < right){
            int mid = left + (right - left)/2;
            merge_recursive(left, mid, nums, temp);
            merge_recursive(mid + 1, right, nums, temp);
            merge(left, mid, right, nums, temp);
        }
    }
    vector<int> sortArray(vector<int>& nums) {
        vector<int> temp(nums.size());
        merge_recursive(0, nums.size() - 1, nums, temp);
        return nums;
    }
};

下面仍旧是一个写好注释的版本：

#include <vector>
using namespace std;

// 归并操作，合并两个有序数组段[arr[left..mid]]和[arr[mid+1..right]]为一个有序数组段[arr[left..right]]
// temp是一个临时数组，用于存储合并后的有序序列，避免直接在原数组上操作导致的数据错乱
void merge(vector<int>& arr, int left, int mid, int right, vector<int>& temp) {
    int i = left; // 左半部分的起始位置
    int j = mid + 1; // 右半部分的起始位置
    int k = 0; // temp数组的当前索引

    // 遍历两个数组，按顺序选择较小的元素放入temp中
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
        }
    }

    // 如果左半部分还有剩余，将剩余元素复制到temp中
    while (i <= mid) {
        temp[k++] = arr[i++];
    }

    // 如果右半部分还有剩余，将剩余元素复制到temp中
    while (j <= right) {
        temp[k++] = arr[j++];
    }

    // 将排序后的temp数组复制回原数组arr
    for (i = left, k = 0; i <= right; i++, k++) {
        arr[i] = temp[k];
    }
}

// 递归执行归并排序
// left是数组段的起始位置，right是数组段的结束位置
void mergeSortRecursive(vector<int>& arr, int left, int right, vector<int>& temp) {
    if (left < right) { // 如果当前数组段不是单元素
        int mid = left + (right - left) / 2; // 计算中间位置
        // 递归排序左半部分
        mergeSortRecursive(arr, left, mid, temp);
        // 递归排序右半部分
        mergeSortRecursive(arr, mid + 1, right, temp);
        // 合并两个有序的部分
        merge(arr, left, mid, right, temp);
    }
}

// 归并排序的主函数，返回排序后的数组
vector<int> sortArray(vector<int>& nums) {
    vector<int> temp(nums.size()); // 创建一个临时数组，大小与原数组相同
    mergeSortRecursive(nums, 0, nums.size() - 1, temp); // 从整个数组的范围开始递归排序
    return nums;
}

3.在排好试卷以后……

鼠鼠希望找到更加高效的方法，于是深入学习了冒泡排序、快速排序、堆排序、选择排序、希尔排序、桶排序和基数排序。在这里与大家分享学习心得，让大家加入鼠鼠大家庭 更快地排序。

对于桶排序、基数排序、希尔排序，不打算写代码，所以浅讲思路。

3.1 桶排序：

假设我们有一组0到99的数字，我们用10个桶来对它们进行排序，每个桶负责一个范围：0-9, 10-19, …, 90-99。将数字根据它们的十位数分配到对应的桶中。
每个桶里面，再进行排序，这里随便你选用什么算法，最好还是插入排序，又稳定，又适应小数据集。这样，每个桶内都是有序的。如果选择插入排序，那么顺带着整个桶排序都是稳定的。
此时再对桶间进行排序。由于每个桶对应的数字范围是不重叠的，我们只需要按桶的顺序依次将桶内的元素合并起来，就可以得到一个有序数组，所以桶间不需要排序。

3.2 基数排序

假设有很多长度相同的数字，我们有0-9 一共10个桶。个位为1的全放到桶1，为2的全放到桶2，……按个位排好了再去排十位，百位。排到最后一位，就是全部有序的了。

3.3 希尔排序

希尔排序是插入排序的升级版，它的优势在于能够快速地把较大的数放到该去的位置附近。第一次排序以较大的一个数x作为间隔，相隔x的数都收集起来进行一个插入排序；然后间隔减小，再插入排序；最后间隔减小到1，此时就已经基本上完全有序了。这个解释不清楚，需要看动图理解。此处略过。

4. 冒泡排序、快速排序、选择排序、堆排序

4.1 冒泡排序

使用flag来标明排好序，也就是说在一次遍历的过程中没有发生任何交换。注意，看代码是从j开始看，外层的i仅仅用来表明j应该到哪里结束（每一次循环，把最大的放到nums的尾部，这样尾部就不用参加两两交换的过程了。）

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int n = nums.size();
        bool flag = true;
        for(int i = 0; flag && i < n - 1; ++i){
            bool flag = false;
            for(int j = 0; j < n - i - 1; ++j){
                if(nums[j] > nums[j + 1]){
                    flag = true;
                    // swap(nums[j], nums[j + 1]);
                    nums[j] = nums[j]^nums[j + 1];
                    nums[j + 1] = nums[j] ^ nums[j + 1];
                    nums[j] = nums[j] ^ nums[j + 1];
                }
            }
        }
        return nums;
    }
};

4.2 快速排序

这里我使用了双指针，似乎还有什么单指针，还有随机化、三向之类的用于描述快排算法细分类的写法。我自定义这里为未随机化（因为每次基准选的是最后一位）+二向（我是两个方向，前后夹击），不知道是否正确，总之感觉这是一个比较好理解的代码。
在quickSort函数里，我们定义了partition_id,并且根据这个partition_id左右切分，继续快排，直到start >= end， 也就是说没有计算partition_id的必要了。
再看partition函数，左右指针分别抓取一个不合规的元素(左边指针指着比最后一个元素小的值，右边指针指着一个比最后一个元素大的值)，然后交换，一直到左右指针重叠，或者左指针大于右指针。此时把最后一个元素和左指针指向的元素进行交换（这里如果不懂为什么是左指针指向的，手动排个序试一试吧），返回的partition就是left指针指向的id。

class Solution {
public:
    int partition(int start, int end, vector<int>& nums){
        int pivot = end;
        int left = start;
        int right = end - 1;

        while(1){
            while(left <= right && nums[left] <= nums[pivot]){
                left++;
            }

            while(left <= right && nums[right] > nums[pivot]){
                right--;
            }
            if(left >= right) break;
            swap(nums[left], nums[right]);
            left++;
            right--;
        }

        swap(nums[pivot], nums[left]);
        return left;
    }

    void quickSort(int start, int end, vector<int>& nums){
        if(start < end){
            int partition_id = partition(start, end, nums);
            quickSort(start, partition_id - 1, nums);
            quickSort(partition_id + 1, end, nums);
        }
    }

    vector<int> sortArray(vector<int>& nums) {
        quickSort(0, nums.size() - 1, nums);
        return nums;
    }
};

4.3 选择排序

我宣布选择排序是最简单的排序算法，就是选最小值，放到第一个，选后面最小值，放到第二个。

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        for(int i = 0; i < nums.size(); ++i){
            int min_index = i;
            for(int j = i; j < nums.size(); ++j){
                if(nums[j] < nums[min_index]) min_index = j;
            }
            swap(nums[i], nums[min_index]);
        }

        return nums;
    }
};

4.4 堆排序

堆排序让我很意外时间复杂度是O(nlogn)，其实是不信建堆时间只要O(n)，但是我们对n/2 个节点以它们为根节点的树进行调整，确实是每个只要跟子节点进行比较一下就好了，如果有涉及到子节点调整那也不会增加太多时间(没细看这里)，所以说确实是O(n)的建堆时间。heapSort里先对于非叶子节点一层一层往上调整根为最大，然后如果交换完了则需要对交换的子节点再次调整。heapify即是一个能够把当前i节点视为树根节点，并且保证i节点为树里最大节点、底下节点也满足根最大的一个函数

class Solution {
public:
    void heapify(vector<int>&nums, int n, int i){
        int largest = i;
        int left = 2*i + 1;
        int right = 2*i + 2;
        if(left < n && nums[left] > nums[largest])
            largest = left;
        if(right < n && nums[right] > nums[largest])
            largest = right;
        if(largest != i){
            swap(nums[i], nums[largest]);
            heapify(nums, n, largest);
        }
    }
    
    void heapSort(vector<int>& nums){
        int n = nums.size();
        // 构建最大堆
        for(int i = n/2 - 1; i >= 0; i--){
            heapify(nums, n, i);//nums一共是n个节点，根是第i个节点
        } 
        //堆顶取值
        for(int i = n - 1; i > 0; i--){
            swap(nums[0],nums[i]);
            heapify(nums, i, 0);//剩下要调整的nums一共是i个节点，根是第0个节点
        }
    }
    
    vector<int> sortArray(vector<int>& nums) {
        heapSort(nums);
        return nums;
    }
};

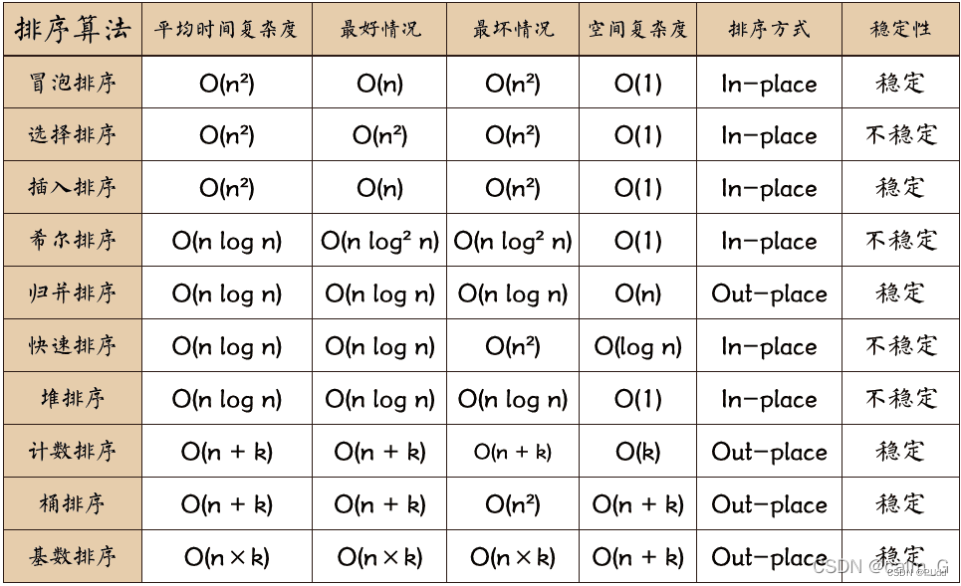
至于稳定性、时间复杂度，鼠鼠又搬运一波