统计-R(相关系数)与R^2(决定系数)
1.相关系数(R)
定义:考察两个事物(在数据里我们称之为变量)之间的相关程度。
假设有两个变量X,Y,那么两个变量间的皮尔逊相关系数可通过以下公式计算:
公式一:
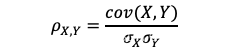
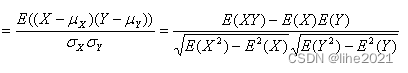
其中,cov是协方差,是X的标准差,是Y的标准差。上述公式可以知道,皮尔逊相关系数是用协方差除以两个变量的标准差得到的。
公式二:
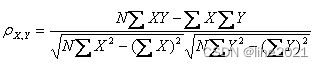
公式三:
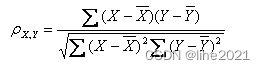
公式四:
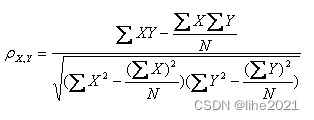
以上列出的四个公式等价,E是数学期望
对关系数的含义可以有如下理解:
(1)当相关系数为0时,X和Y两变量无关系。
(2)当X的值增大(减小),Y值增大(减小),两个变量为正相关,相关系数在0.00与1.00之间
(3)当X的值增大(减小),Y值减小(增大),两个变量为负相关,相关系数在-1.00与0.00之间
(4)相关系数的绝对值越大,相关性越强,相关系数越接近于1或-1,相关度越强;相关系数越接近于0,相关度越弱
2.决定系数(R^2)
定义:对模型进行线性回归后,评价回归模型系数拟合优度。
公式:R2=SSR/SST=1-SSE/SST
SST (total sum of squares):总平方和
SSR (regression sum of squares):回归平方和
SSE (error sum of squares) :残差平方和。
