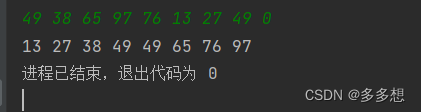
选择排序算法（Selection Sort）原理及实现

选择排序算法，运行效率不高，但是非常容易理解，算法复杂度为  。

原理：

假设要排序的数组的长度为n，将数组先分为两个部分，一个是有序区域部分，另一个为无序区域部分。初始时有序部分中没有元素，所有的元素都在无序区域中。第 1 趟遍历无序区域中的 n 个元素，从中选出最小的元素作为有序区域的第一个元素；第 2 趟遍历无序区域中剩下的 n-1 个元素，选出最小的元素作为有序区域的第二个元素。可以看到每遍历无序区域一遍，就找到其中最小的元素放入有序区的尾部，这样只要遍历n遍就能将无序区域中的所有元素按照顺序放入有序区域中了，也就完成了排序的操作。

代码实现：

#include <stdio.h>

int main() {
    int a[10];
    int n = 0, i, j, k, t;
    while (scanf("%d", &a[n])) {//输入任意个数字，遇到0时结束输入，记录个数n
        if (a[n] == 0) break;
        n++;
    }
    for (i = 0; i < n - 1; i++) {//选择排序，遍历n-1遍
        // 从数组开头到第i个元素的区间为有序区域, 无序区域紧接着有序区域
        // 内层循环就是遍历无序区域找到无序区域中最小的元素
        for (j = i + 1, k = i; j < n; j++) {//a[k]记录无序区域中最小元素，k为最小元素的下标
            if (a[j] < a[k]) k = j;
        }
        if (k != i) { // 如果最小值不是第i个元素，则将 a[i] 和 a[k]交换
            t = a[i];
            a[i] = a[k];
            a[k] = t;
        }
    }
    for (i = 0; i < n; i++) {
        printf("%d ", a[i]);
    }
    return 0;
}

可以看出代码的实现并没有遍历 n 遍，而是 n-1 遍，这是因为当无序区域中剩下最后一个元素的时候，该元素是在有序区域之后的，即最后无序区域剩下一个元素时数组已经是有序的了。