当前位置：首页 > article >正文

视频：Python深度学习量化交易策略、股价预测：LSTM、GRU深度门控循环神经网络|附代码数据...

article 2024/11/15 5:38:48

全文链接：https://tecdat.cn/?p=37539

分析师：Shuo Zhang

本文以上证综指近 22 年的日交易数据为样本，构建深度门控循环神经网络模型，从股价预测和制定交易策略两方面入手，量化循环神经网络在股票预测以及交易策略中的效果，结合一个Python深度学习股价预测、量化交易策略：LSTM神经网络的代码和数据，为构建神经网络股票预测以及量化交易模型提供参考信息（点击文末“阅读原文”获取完整代码数据）。

讲解视频

关键词：深度门控循环神经网络；股票市场；股价预测；交易策略

研究背景与意义

（一）研究背景
随着科技的进步，大量的金融数据得以保留，为股票市场的分析提供了坚实的数据基础。同时，算法的不断发展更新，为人们分析股票市场提供了强有力的工具。研究者们正在不断探索机器学习、深度学习方法在股票市场上的应用。

（二）研究意义
本文通过构建深度门控循环神经网络模型，量化其在股票预测以及交易策略中的效果，期望能为构建神经网络股票预测以及量化交易模型提供一些可供参考的信息。

人工神经网络

常见的神经网络模型由输入层、隐藏层和输出层组成，如图所示。图中的每一个圆圈都表示一个神经元，每一个神经元都与下一层的神经元连接，这种神经网络也被称之为全连接神经网络。

深度神经网络

在简单的神经网络中增加隐藏层的层数，同时增加隐藏层神经元的个数，可得到深度神经网络（DNN）。相较于简单的神经网络，深度神经网络有着更加复杂的结构，且随着隐藏层个数或隐藏层神经元的不断增加，深度神经网络也会变得越来越复杂。

神经网络的正向传播

以一个神经元模型为例，该模型包含输入、输出以及计算单元。其中 x 为输入，w 为权重，output 为输出，是激活函数。神经网络的正向传播过程就是通过一层一层计算和传递，最后得到一个输出结果的过程，可用于解决实际中关于分类或者预测的问题。

神经网络的反向传播

反向传播过程是将预测值与真实值反向传播回去，从而调整神经网络模型中的权重参数的过程。进行反向传播时，需先定义一个损失函数来度量预测值和真实值之间的偏离程度，本文采用均方误差为损失函数。在反向传播过程中调整权重参数通常采用梯度下降法，该方法实际就是一个不断求导的过程，首先对损失函数进行求导，然后让参数按着导数的方向变化，之后不断重复这个过程。

激活函数

（一）ReLU 函数
ReLU 函数只保留正数元素，并清除负数元素，是一个简单的非线性变换。

（二）sigmoid 函数
sigmoid 函数能够将输入变成在 0 到 1 之间的值，当输入的值在 0 的附近时，该函数近似于线性变换。

（三）tanh 函数
tanh 函数也被称为双曲正切函数，它可以把输入的值变换到 -1 到 1 之间。

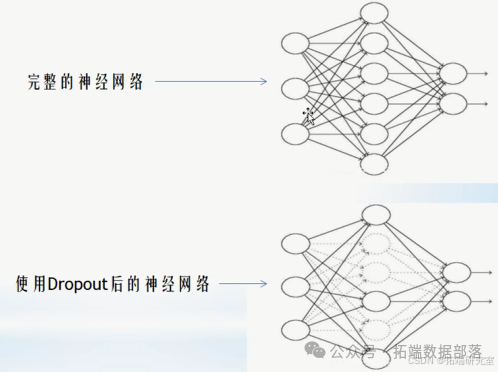
丢弃法

在模型的训练过程中，可能会出现过拟合和欠拟合的问题。过拟合是指模型在训练集中表现良好，而在测试集中表现变差；欠拟合可能是由于模型的复杂程度不够，可以考虑增加模型的层数或者隐藏层的单元数。过拟合时需要对模型进行正则化，正则化可以很好地应对过拟合。丢弃法（又称 dropout）通过在训练时以一定概率丢弃神经元来简化模型，从而起到正则化的作用。

循环神经网络

如图所示，左边为神经网络模型，右边为循环神经网络模型。X 表示输入，Y 表示输出，中间部分都是隐藏层。二者的不同之处在于隐藏层是否存在虚线，在循环神经网络模型中，这个虚线的功能就是维护一个状态，使得这个状态可以作为下一时刻的输入。也就是说，当前时刻的输入不仅与当前时刻的输入 X 有关，而且还与上一时刻的隐藏状态有关。

深度循环神经网络

深度循环神经网络即有多个隐藏层的循环神经网络。其中每个隐藏状态不仅传递给当前时间步的下一层，而且还传递给当前层的下一个时间步。其中 X 为输入，H 为隐藏状态，W 为权数，b 为偏差项，O 为输出，p 为激活函数。第 1 层的隐藏状态的计算公式没有变化，而其它隐藏层的隐藏状态的计算公式会发生变化。到最后，只需要基于最后一层即第 L 隐藏层的隐藏状态去计算输出层的输出。将隐藏层单元换为 LSTM 单元就可得到深度门控循环神经网络模型。

LSTM 神经网络

长短期记忆门控循环神经网络（LSTM）是一种对 RNN 的改进网络。它在神经网络中引入了门控机制，即输入、遗忘和输出门。

LSTM 神经网络的训练步骤

（一）第一步：设计 LSTM 的模型网络结构，建立好 LSTM 模型，并选择好所需的损失函数。

（二）第二步：建立好模型以后，需要初始化模型参数，通过前向计算求解出模型的估计值，并根据估计值和真实值计算出模型的损失函数值。

（三）第三步：根据损失函数对参数求导计算参数的梯度信息，根据模型的学习率和梯度信息来更新模型参数（学习率过大会导致模型难以收敛，学习率过小模型收敛速度又会过慢），并将新的参数重新带入模型进行数据信息的前向计算。

（四）最后：通过第二、三步的循环计算，我们最终可以确定模型参数，建立出合适的 LSTM 模型，应用于实际的分类或预测中。

数据的处理和分析

本文主要介绍了股票数据的收集、预处理、分析以及深度门控循环神经网络模型在股票市场中的应用，包括数据的划分、LSTM 的适用性研究、超参数的选择和优化、预测结果分析及评估以及量化交易策略的制定等内容。

（一）数据收集

本文通过引入 python 中的 tushare 库来收集上证综指从 2000 年初到 2021 年末的日交易数据，包括 date（数据日期）、open（开盘指数）、close（收盘指数）、high（最高指数）、low（最低指数）以及 volume（成交量），共有 5332 条数据。
股票价格指数可以反映股市总体价格水平的变化，对所在市场的运行状况有很好的敏感性。股票价格指数上升表明股票的平均价格水平上涨，反之则下降。

（二）数据分析

使用 python 对上证综指的收盘指数进行描述性统计分析，包括均值、中位数等，同时绘制收盘指数的走势图。分析可知收盘指数的偏度为 0.62，为中度右偏分布；峰度为 0.64，为尖峰分布，该分布不为也不近似于正态分布。

（三）数据的划分

在应用神经网络模型进行分类或预测时，需将数据划分为训练集、验证集以及测试集。本文按照 8:2 的比例将上证综指的数据分为训练集和测试集，并将训练集的 10% 作为验证集，用于检验模型的性能并调整参数。

（四）LSTM 的适用性研究

利用上证综指的收盘指数数据集对 LSTM 模型在股市中的适用性进行研究。将数据集按照 8:2 的比例划分为训练集和测试集，训练集的 10% 作为验证集。分别使用 ANN 模型和 LSTM 模型对数据进行训练验证和预测，优化器都使用 Adam，激活函数都为 ReLU 函数，都使用均方误差 MSE 作为损失函数。由结果可知 LSTM 模型的最终验证误差更小。

（五）超参数的选择和优化

超参数是在训练前人为设置的参数，不同的超参数对模型性能影响很大，因此需要进行优化。本文使用网格搜索的方法对神经网络模型进行超参数优化，确定几个候选超参数，给出取值范围，遍历所有可能的组合，找到使验证集损失值最小的组合。
经过实验，调整窗口大小分别为 10、20、50，当窗口大小为 50 时整体表现最好，故选择 50 为窗口大小；再进行试验发现训练 50 轮之后训练误差仍有小幅度减小，故选取 100 作为训练轮数。如右表所示，为模型设定的所有具体超参数组合以及在该组合下模型的最低验证误差 (val loss)，当有 2 层 LSTM 隐藏层，神经元个数为 50，丢弃率为 30%，batch_size 为 64 时，模型获得相对最小的验证误差。

（六）预测结果分析及评估

构建深度门控循环神经网络模型后，利用训练集训练模型，代入测试集进行预测，将预测值反归一化变为正常数据并与真实值比较，最后将结果可视化。

点击标题查阅往期内容

R语言对S＆P500股票指数进行ARIMA + GARCH交易策略

左右滑动查看更多

（七）量化交易策略的制定

制定量化交易策略为：定义目标变量 Price Rise，当明日收盘价大于当日收盘价则赋值为 1，否则赋值为 0。按 8:2 划分训练和测试集。经过多次试验，将使用最高价与最低价之差、收盘价与开盘价之差、5 天的标准差、3 日均线、10 日均线、30 日均线、相对强弱指数、威廉姆斯指标等 8 个特征作为输入去训练模型并对测试集进行预测，若预测值大于 0.5 则在当日结束时持多头头寸并在第二日结束时平仓，反之则持空头头寸并在第二日进行平仓。

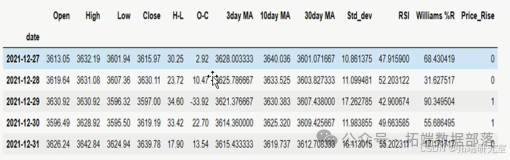
在制定交易策略阶段仍用网格搜索的方法选取超参数，模型选取的超参数如下：2 层 LSTM 隐藏层、每个 LSTM 层 50 个神经元、LSTM 层激活函数为 ReLU、最后一层全连接层激活函数为 Sigmoid、优化器为 Adam、Dropout 取 20%、损失函数为 MSE，batch size 为 20、训练轮数 epochs 为 100，在模型训练阶段又新加入了模型评估指标准确率 accuracy。由于更换了输入特征，在数据缩放阶段经过多次试验发现标准化的效果要比归一化效果更好，故在数据预处理时对数据进行了标准化处理。

最后让本文制定的交易策略（策略一）的累计收益与在今天结束时持有多头头寸并在第二天结束时平仓（策略二）这样一个策略的累计收益进行对比。为便于计算和对比，本文计算的收益都为对数收益，即今天的收盘价除以昨天的收盘价的对数。由结果可知本文的策略收益较为可观，但由于每天都要交易，交易频率较高，故该模型在交易佣金较高的股票中表现可能会较差。

Python深度学习股价预测、量化交易策略：LSTM神经网络|附代码数据

股价预测

本文对股票数据进行了分析和处理，通过计算指数移动平均值、定义超参数、监测测试均方误差等方法构建了股票预测模型，并对预测结果进行了可视化展示。

数据展示与处理

首先，我们查看了股票数据的头部信息（spy.head()）。然后，通过设置图形参数，绘制了特定股票数据的折线图，其中横坐标为数据索引，每隔 500 个数据点显示一个标签，并将标签旋转 45 度，纵坐标为股票数据的特定列值。

spy.head()

plt.xticks(range(0,df.shape\[0\],500),df.index\[::500\],rotation=45)plt.plot(df\[column\])

指数移动平均计算

接下来，计算了指数移动平均值（EMA）。初始时，EMA 设为 0.0，设定衰减因子 gamma 为 0.1。通过遍历数据集中的每个时间点，根据公式 EMA = gamma*train_data[ti] + (1-gamma)*EMA 不断更新 EMA 值，其中 train_data[ti] 表示当前时间点的原始数据值。

EMA = 0.0gamma = 0.1for ti in range(4907):EMA = gamma\*train\_data\[ti\] + (1-gamma)\*EMAtrain\_data\[ti\] = EMA

超参数定义

为了构建深度长短期记忆（LSTM）模型，定义了一系列超参数。数据的维度 D 设为 1，表示数据的单一特征维度。设定未来观察的时间步数为 num_unrollings = 50，即模型将考虑未来 50 个时间步的情况。批量大小 batch_size 设为 500，表示每次训练时使用的样本数量。定义了隐藏层节点数量列表 num_nodes = [250,200,100]，表示深度 LSTM 堆栈中每个层的隐藏节点数量，总层数 n_layers 为隐藏层节点数量列表的长度。设置 dropout 比例为 0.2，以防止过拟合。

D = 1 # Dimensionality of the datanum\_unrollings = 50 # Number of time steps looking into the future.batch\_size = 500 # Number of samples in a batchnum\_nodes = \[250,200,100\] # Number of hidden nodes in each layer of the deep LSTM stackn\_layers = len(num_nodes) # number of layersdropout = 0.2 # dropout amount

模型训练与监测

在模型训练过程中，持续监测测试集的均方误差（MSE）。如果当前测试 MSE 大于已记录的测试 MSE 列表中的最小值，则增加损失非递减计数。如果当前测试 MSE 小于或等于已记录的最小值，则将损失非递减计数重置为 0。当损失非递减计数超过设定的阈值时，增加训练步数并重置损失非递减计数。最终，得到最低的测试 MSE 值为 round(min(test_mse_ot), 5)。

if len(test\_mse\_ot)>0 and current\_test\_mse > min(test\_mse\_ot):loss\_nondecrease\_count += 1else:loss\_nondecrease\_count = 0if loss\_nondecrease\_count > loss\_nondecrease\_threshold :session.run(inc\_gstep)loss\_nondecrease_count = 0
``````
round(min(test\_mse\_ot), 5) #MSE

预测结果可视化

确定最佳预测时期为第 9 个 epoch。通过绘制图形展示预测结果随时间的演变。首先，设置图形尺寸为 (18,18)，并分为两个子图。在第一个子图中，绘制了所有中间数据的折线图，颜色为蓝色。对于预测结果，随着时间的推移，旧的预测使用较低的透明度，新的预测使用较高的透明度。从初始透明度 start_alpha = 0.25 开始，根据预测数量逐步增加透明度，使得预测结果的演变更加直观。横坐标限制在特定的数据范围 (4907,5032)，以便更好地观察预测结果在特定时间段的变化。

best\_prediction\_epoch = 9alpha  = np.arange(start\_alpha,1.1,(1.0-start\_alpha)/len(predictions\_over\_time\[::3\]))for p\_i,p in enumerate(predictions\_over\_time\[::3\]):for xval,yval in zip(x\_axis\_seq,p):plt.plot(xval,yval,color='r',alpha=alpha\[p\_i\])

股票市场交易策略分析 —— 基于 LSTM 模型与其他方法的比较

本文利用从 1973 年 1 月 1 日至 2011 年 3 月 31 日的标准普尔 500 指数数据，通过定义函数计算毛收益率和净收益率，构建了 LSTM 模型以决定在测试期间每月的第一天是否进入市场。同时，将 LSTM 方法与买入持有策略和移动平均策略进行比较，以评估不同策略在股票市场中的表现。

数据获取

使用雅虎财经获取了从 1973 年 1 月 1 日至 2011 年 3 月 31 日的标准普尔 500 指数数据。由于在当前环境中无法直接使用雅虎财经，故将数据保存为 “GSPC.csv” 文件。分析基于月度数据进行，且所有决策都在每月的第一个交易日做出。出于某种原因，分析将从 1973 年 1 月后的 24 个月开始，并在 2011 年 3 月的前一个月结束。对数据进行重采样，以月为单位计算平均值（dfm = df.resample("M").mean()）。

dfm=df.resample("M").mean()

二、定义计算毛收益率和净收益率的函数

注意到可以使用特征 “rapp” 非常容易地计算毛收益率。以下函数解释了如何计算：向量v选择我们将在市场中停留的月份。

三、定义 LSTM 模型

我们希望使用 LSTM 神经网络在测试期间的每个月的第一天决定是否在该月留在市场中。对数据进行重塑（LSTM 模型需要特定形状的数据，涉及 “窗口”），并且在每个步骤中，我们希望预测下个月第一天的开盘价格。通过这种方式，我们能够找到向量v，它选择了我们将在市场中停留的月份。

model=model\_lstm(window+1,8)history=model.fit(X\_trainw,y\_traiplt.plot(history.history\['loss'\])plt.plot(history.history\['val\_loss'\])plt.title('model loss')plt.ylabel('loss')plt.xlabel('epoch')plt.legend(\['train', 'test'\], loc='upper right')plt.show()

构建 LSTM 模型（model = model_lstm(window + 1, 8)），并使用训练集和验证集进行训练（history = model.fit(X_trainw, y_trainw, epochs=500, batch_size=24, validation_data=(X_testw, y_testw), verbose=0, callbacks=[], shuffle=False)）。绘制模型的训练损失和验证损失随 epoch 的变化曲线，以观察模型的训练情况。

当预测的下个月价格大于当前价格时，我们留在市场中，否则退出市场。向量v表示 “在市场中的月份”（用 1 表示）和 “不在市场中的月份”（用 0 表示）。

前面的图展示了我们模型预测的一个有趣特征：它在预测指数一阶导数的符号方面相当出色，而这正是我们的交易策略所需要的。

比较 LSTM 方法与其他方法

现在可以将我们的 LSTM 交易策略与买入持有策略和移动平均策略进行比较。为了进行比较，我们计算相应的向量v_bh和v_ma，它们选择了我们将在市场中停留的月份。

结论

本文通过对股票数据的一系列处理和分析，构建了基于深度 LSTM 的股票预测和量化策略模型，并通过可视化展示了预测结果的演变。然而，该模型仍有进一步改进的空间，例如优化超参数选择、引入更多的特征工程等，以提高股票预测的准确性和稳定性。未来的研究可以继续探索更先进的机器学习和深度学习方法，为股票市场的预测和投资决策提供更有力的支持。