基本滤波器响应(低通+高通+带通+带阻)+滤波器的响应特性(阻尼系数+截止频率下降率)
2024-9-4,星期三,20:40,天气:晴,心情:多云。又是上班的一天,至于心情为什么多云,是因为女朋友换季感冒了,我有上班回不去,难受,赶紧到周五吧,我要回去看我的宝宝了!!!其他没啥说的,加油上班,加油学习。
今天开始了第九章的学习,主要学习内容为:基本滤波器响应(低通+高通+带通+带阻)+滤波器的响应特性(阻尼系数+截止频率&下降率)
一、有源滤波器
滤波器可以让某些特定频率的输入信号达到输出端,而让其他频率的输入信号不能通过,这种特性称为选择性。有源滤波器使用的元件包括带无源RC、RL、RLC网络的晶体管或运算放大器,其中,有源器件提供电压增益,无源网络由于频率选择,一般根据响应,有源滤波器分为低通、高通、带通和带阻四种类型。
1. 基本滤波器响应
(1)低通滤波器响应:一个滤波器的通带是其允许通过的频率区域,这些区域中的信号损耗最小(通常定义为小于-3dB);截止频率fc定义为通带的末端频率,通常指响应自通带开始下降3dB(70.7%)的位置;通带后的位置称为过渡区;过渡区后是阻带,过渡区和阻带之间没有精确的分界点。
低通滤波器允许从直流到fc之间的频率通过并使其他频率的信号大幅衰减,理想低通滤波器的通带如下图所示,当频率处于通带以外时响应降为0,理想低通滤波器的带宽BW = fc。
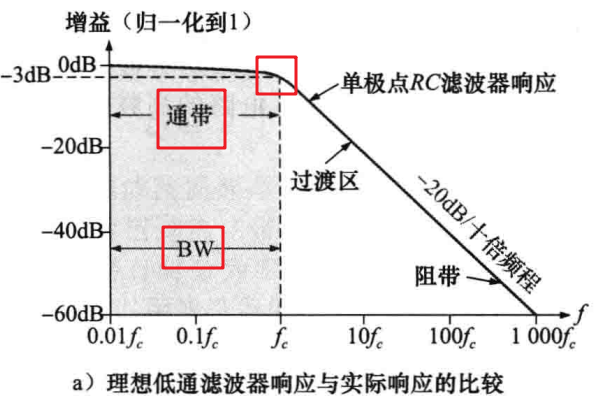
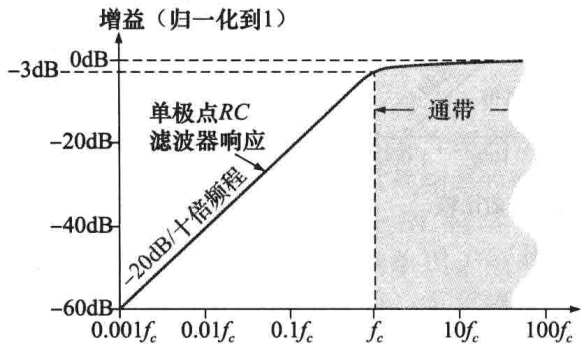
任何实际的滤波器都不可能实现如上图所示的理想响应,实际滤波器的响应取决于极点的数量,极点表示的是滤波器所包含的旁路电容的数量,大部分基本低通滤波器是一个简单的RC电路,仅由一个电容和一个电阻组成,输出在电容上产生,如下图所示,这种基本RC滤波器具有一个单极点,超过截止频率后增益一-20dB/十倍频程的速度衰减(在上图中画出),在通带范围内,其增益几乎是常量,超过截止频率后,增益以固定的下降率迅速下降。
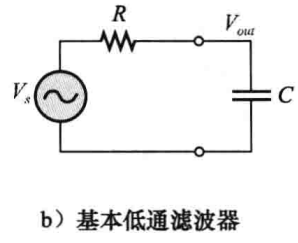
基本RC滤波器增益以-20dB/十倍频程下降意味着在10fc频率处,输出是输入的-20dB(10%),但是这种平缓的下降并不是很好的滤波器特性,因为会使更多不期望的频率信号通过该滤波器。
简单低通滤波器的截止频率位于XC = R处,其中,fc = 1 / 2ΠRC,根据基本电路原理可以知道,截止频率处的输出是输入的70.7%,这种响应等价于衰减了-3dB。下图给出了几种理想低通响应曲线,包括基本单极点响应(下降率-20dB/十倍频程),从图中可以看出,理想低通滤波器在其通带内的响应食分平坦,但实际情况下的通带响应并没有那么平坦,在截止频率处会有-3dB的衰减。
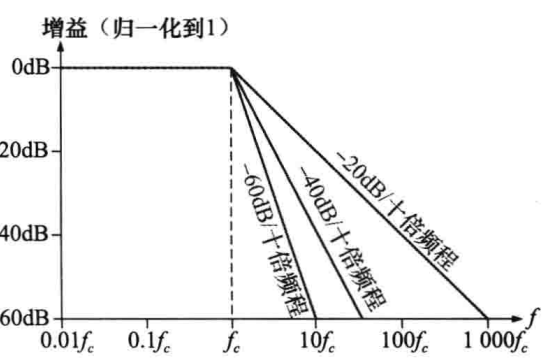
通过将运算放大器与频率选择反馈网络进行组合,设计后的滤波器的下降率可以达到-40dB/十倍频程、-60dB/十倍频程甚至更大,一般把这种包含一个或多个运算放大器的滤波器称为有源滤波器,通常,滤波器使用的极点越多,滤波器相应的过渡区越陡,滤波的效果会越好。
(2)高通滤波器响应:高通滤波器可以极大衰减或不让低于fc的频率信号通过,并让所有高于fc的频率信号通过,如下图所示,同样的,在截止频率处的输出为通带的-3dB(70.7%),理想的响应由图中的阴影区标出,理想情况下,高通滤波器的的通带由大于截止频率的所有频率组成,但实际电路中高频响应受到运算放大器或其他元件的限制。
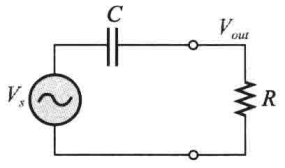
基本高通滤波器同样由一个RC网络组成,与低通滤波器不同的是,高通滤波器的输出取自电阻,如下图所示:
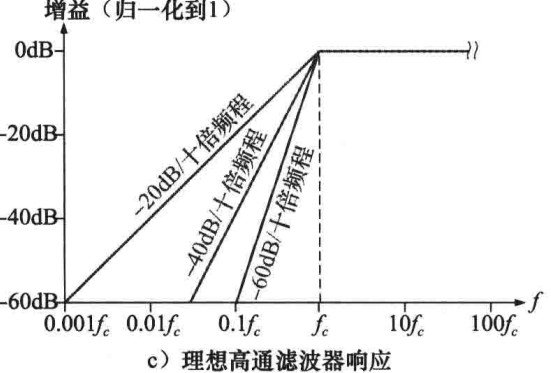
下图展示了几种理想的高通滤波曲线,与低通滤波曲线类似,基本高通滤波器的截止频率发生在XC = R处,此时fc = 1 / 2ΠRC,高通滤波器的滤波效果同样取决几点个数和滤波器类型:
(3)带通滤波器:带通滤波器允许位于下限频率和上线频率之间的信号,阻止给定带宽以外的信号,带宽定义为上截止频率(fc2)和下截止频率(fc1)的差:BW = fc2 - fc1,下图为一基本带通滤波器的响应曲线:
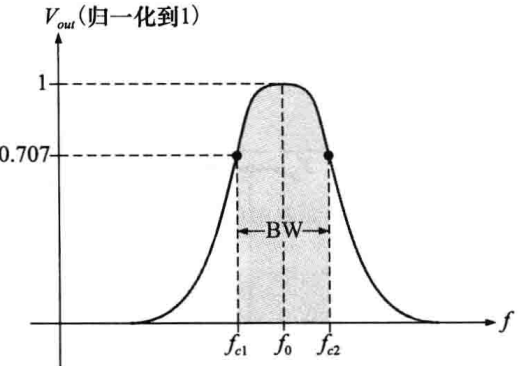
上下截止频率均为响应曲线降到其最大值的70.7%处的频率点(3dB频率),带宽中心的频率称为中心频率f0,其定义为上下截止频率的几何均值,即f0 = (fc1fc2)1/2。
-
品质因数:滤波器的品质因数定义为中心频率和带宽之比,即Q = f0 / BW,当f0一定时,Q的值越高,带宽越窄且选择性越好。带通滤波器根据带宽大小分为窄带(Q > 10)或宽带(Q < 10),Q也可以用滤波器的阻尼系数表示,Q = 1 /DF,后面会详细介绍。
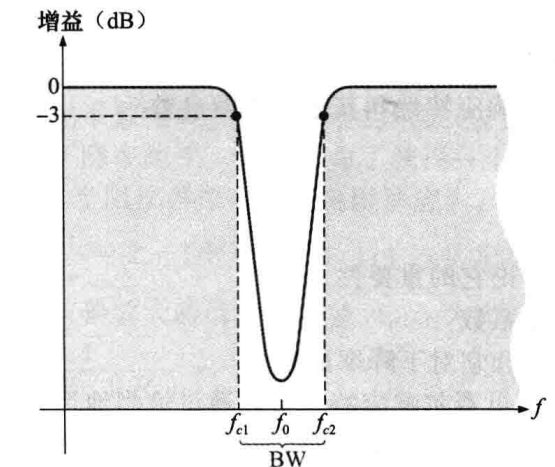
(4)带阻滤波器:带阻滤波器也称陷波滤波器、频带抑制滤波器等,其一般响应曲线如下图所示,带宽是3dB频率点之间的宽度,可以简单的理解为带阻滤波器与贷款滤波器的功能相反,即在带宽范围内的信号会被过滤,而在带宽范围外的信号会通过。
2. 滤波器的响应特性
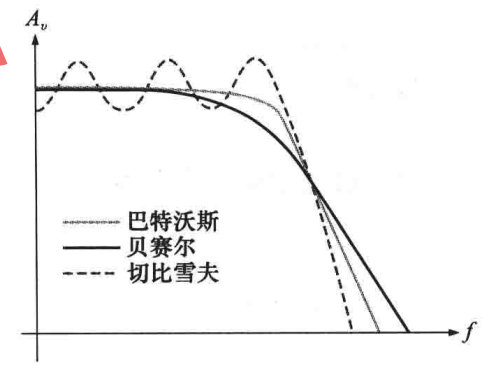
上面学习的每种滤波器可以通过选择恰当的有源滤波器电路的元件值来实现不同的巴特沃斯、切比雪夫或贝塞尔特性,每一种特性都是由响应曲线的形状来进行划分的,每种特性在特定的应用中都具有各自的优势。
-
巴特沃斯特性:巴特沃斯特性曲线在通带内可以提供近乎定值的幅值响应,并且下降率为-20dB/十倍频程/每极点,具有这种特性的滤波器的相位响应是非线性的,但是,通过滤波器的信号相移会随着频率而非线性变化(因此具有时延),因此,加到巴特沃斯响应的滤波器上的脉冲输入将在输出端引起超调,因为脉冲上升沿和下降沿中的每个频率分量经历了不同的时延。具有巴特沃斯响应的滤波器通常用于当通带内的所有频率必须具有相同增益时。
-
切比雪夫特性:具有切比雪夫特性的滤波器常用于要求下降率很快的情况下,因为其可以提供大于-20dB/十倍频程/每极点的下降率,所以对于给定的下降率,滤波器可以用较少的极点和较简单的电路来实现,但是,这种类型的滤波器响应在通带内会产生超调和波动(取决于极点的数量),产生的线性相移也比巴特沃斯特性滤波器少。
-
贝塞尔特性:贝塞尔响应具有线性位移特性,即相移随着频率线性增加,这可以使脉冲输入信号的响应几乎没有超调,因此,贝塞尔特性滤波器常被用于过滤脉冲波形,因为不会产生波形失真
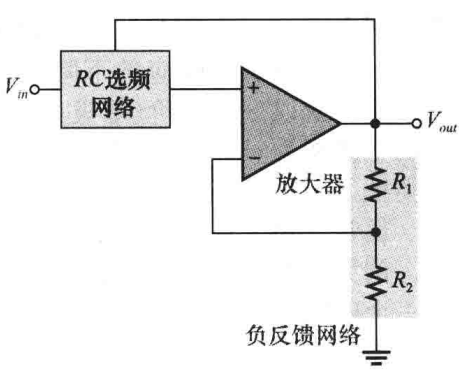
(1)阻尼系数:有源滤波器电路的阻尼系数DF决定了这个滤波器呈现以上三种特性中的哪一种,为了解释DF的概念,下图给出了一个广义的有源滤波器,其包含一个放大器,一个负反馈网络和一个滤波器部分。在一个同相放大器中,放大器和反馈网络相连,阻尼系数有负反馈网络决定,定义为DF = 2 - (R1 / R2):
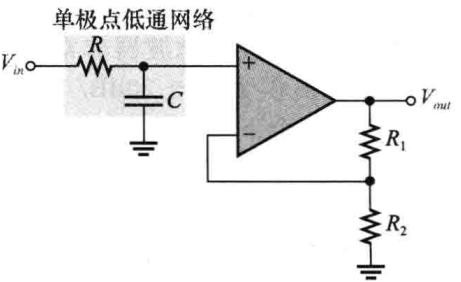
(2)截止频率和下降率:截止频率由RC网络中的电阻和电容值决定,如下图所示,一个单极点(一阶)滤波器,截止频率为:fc = 1 / 2ΠRC:
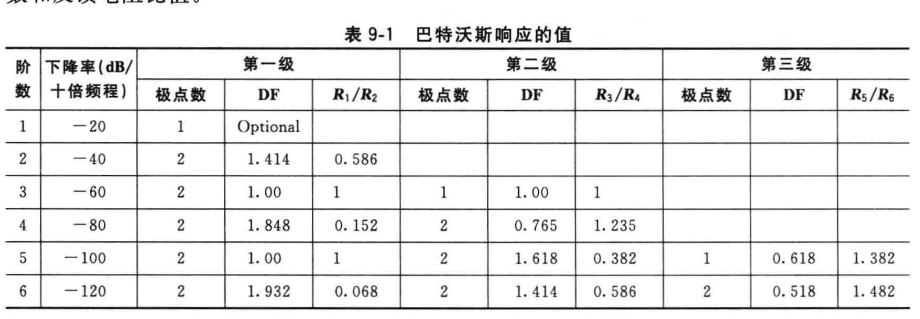
对于一个单极点高通滤波器来说,截止频率的计算方法是相同的,极点数量决定滤波器的下降率,一个巴特沃斯响应的下降率使-20dB/十倍频程/每极点,则单极点(一阶)巴特沃斯响应的下降率为-20dB十倍频程,二极点(二阶)巴特沃斯响应的下降率为-40dB十倍频程,以此类推。为了获得三阶以上的滤波器,通常会采用单极或两级滤波器级联组成,如下图所示:
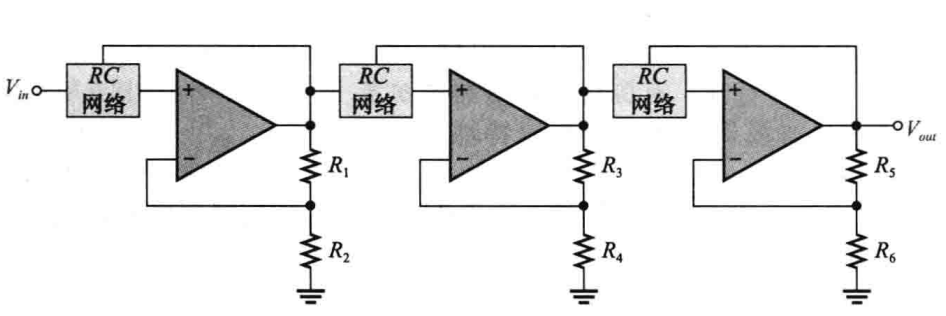
例如,为了得到一个三阶滤波器,将一个二阶滤波器和一个一阶滤波器级联起来,为了得到四阶滤波器,将两个二级滤波器级联。一般在设计时可以通过查表确定夫反馈电阻的阻值,以巴特沃斯响应滤波器为例: