算法复盘——Leetcode hot100:链表160
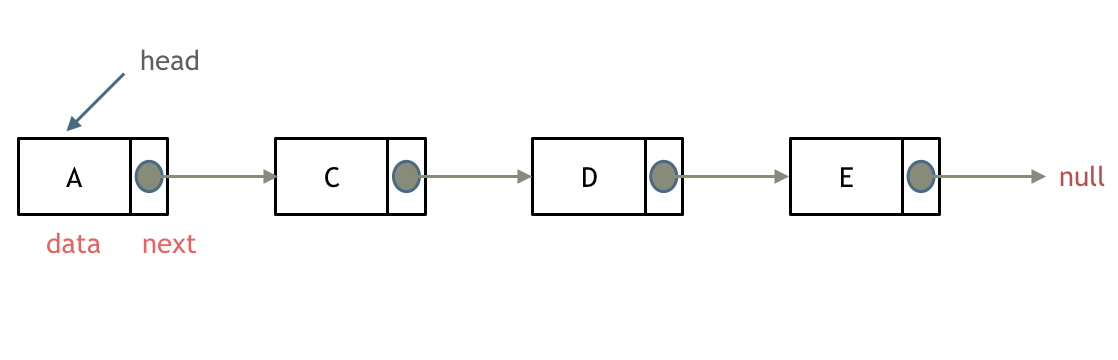
链表
- 链表是一种在物理存储上非连续的结构,数据元素的逻辑结构通过引用链接次序实现
- 结点 一般都是从堆上申请出来的
- 从堆上申请的空间,可能连续可能不连续
- 链表的结构有8种
- 单向或双向
- 带头或者不带头
- 循环或者非循环
- 无头单向非循环
- 无头双向链表
链表常用技巧和操作
- 技巧
- 画图!!!
- 引入虚拟“头”节点
- 不要吝啬空间,大胆去定义变量
- 快慢双指针
- 链表中的常用操作
- 创建一个新节点
- 尾插
- 头插 方便逆序链表
ArrayList和LinkedList的区别

- 面试时需要自己写链表的定义
public class ListNode{
// 结点的值
int val;
// 下一个结点
ListNode next;
// 节点的构造函数(无参)
public ListNode(){
}
public ListNode(int val){
this.val = val;
}
public ListNode(int val,ListNode next){
this.val = val;
this.next = next;
}
}
160. 相交链表 - 力扣(LeetCode)
头脑风暴ing:完全没思路…相交 一样 .next=.next 虽然是简单,但是接触链表第一题完全没思路,直接看的题解~
就是求两个链表交点节点的指针。 交点不是数值相等,而是指针相等。
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode cur1 = headA;
ListNode cur2 = headB;
while(cur1 != cur2){
if(cur1 == null){
cur1 = headB;
}else{
cur1 = cur1.next;
}
if(cur2 == null){
cur2 = headA;
}else{
cur2 = cur2.next;
}
}
return cur1; 当cur1 == cur2时,它们要么都指向相交节点,要么都指向null
}
}
代码解释
-
初始化:定义两个指针
cur1和cur2,分别指向headA和headB。 -
循环:使用一个while循环,直到
cur1和cur2相等(即找到相交节点或者都为null)。 -
指针移动
:
- 如果
cur1到达链表A的末尾(即cur1 == null),将其重新指向链表B的头节点。 - 否则,将
cur1移动到下一个节点。 - 对
cur2执行类似的操作,如果到达链表B的末尾,则重新指向链表A的头节点。
- 如果
-
返回结果:当
cur1和cur2相等时,退出循环,它们要么都指向相交节点,要么都指向null(表示不相交)。
这种算法的时间复杂度为O(n + m),其中n和m分别是链表A和链表B的长度,因为每个节点最多被访问两次。空间复杂度为O(1),因为只使用了常量级别的额外空间。
代码简化:三元条件运算符
while (cur1 != cur2) {
// 如果cur1到达链表A的末尾,将其重定向到链表B的头节点
cur1 = (cur1 == null) ? headB : cur1.next;
// 如果cur2到达链表B的末尾,将其重定向到链表A的头节点
cur2 = (cur2 == null) ? headA : cur2.next;
}
三元条件运算符(ternary operator)在Java及许多其他编程语言中是一种简洁的条件表达式语法。它允许你在单行代码中根据条件选择两个值中的一个。三元运算符由 ? 和 : 组成,语法如下:
result = condition ? valueIfTrue : valueIfFalse;
这里:
condition是一个布尔表达式,它返回true或false。valueIfTrue是当condition为true时要返回的值。valueIfFalse是当condition为false时要返回的值。result是整个三元表达式计算后的结果,它的类型与valueIfTrue和valueIfFalse的类型应该相同(或至少能够隐式转换为相同的类型)。
三元运算符可以极大地简化代码,使你在需要基于条件赋值时不必编写完整的 if-else 语句。然而,过度使用三元运算符可能会使代码变得难以阅读,特别是在复杂的逻辑表达式中。
leetcode上有意思的题解

1.这道题的问题就在于A和B虽然相交,但是A和B的长度不同,也就是A和B离终点的距离不一样,这样不公平啊!总有人会先到相交点!
2.为了解决公平问题,我们假设null是轮回传送门,让他们走一条长度大于等于max{A,B}的路径,他们之间走的距离就一样了,既然“距离一样,速度一样,必然会同时到达终点”
3.已知他们一定会同时到达终点,我们只要把终点设在相交点就大功告成了! 于是我们设定《A长度+B长度+相交点到null的长度+1》这样一条必然大于max{A,B}长度,且两次包含相交点的路作为路径
4.那么A和B走这条路径都会先经历一次相交点再经历一次null再回到对方的起点,最终同时走到终点
- 对的人错过了还是会相遇, 错的人相遇了也是NULL!
