排序
一.排序概念及引用
1.排序概念
排序:使一串记录,按照其中某个或某些关键字大小,递增或递减排列起来的操作
稳定性:假定在待排序的序列中,存在多个相同的关键字,若经过排序,这些关键字的前后位置关系没变,则称这种排序是稳定的,否则称为不稳定的
内部排序:数据元素全部存放在内存中的排序
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动的排序
2.常见的排序算法
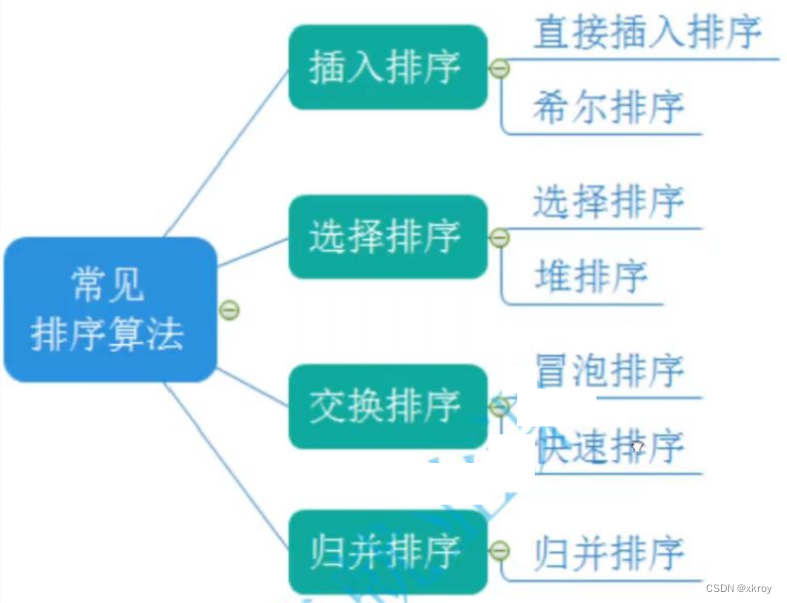
二.常见排序算法的实现
1.插入排序
1.基本思想
2.直接插入排序
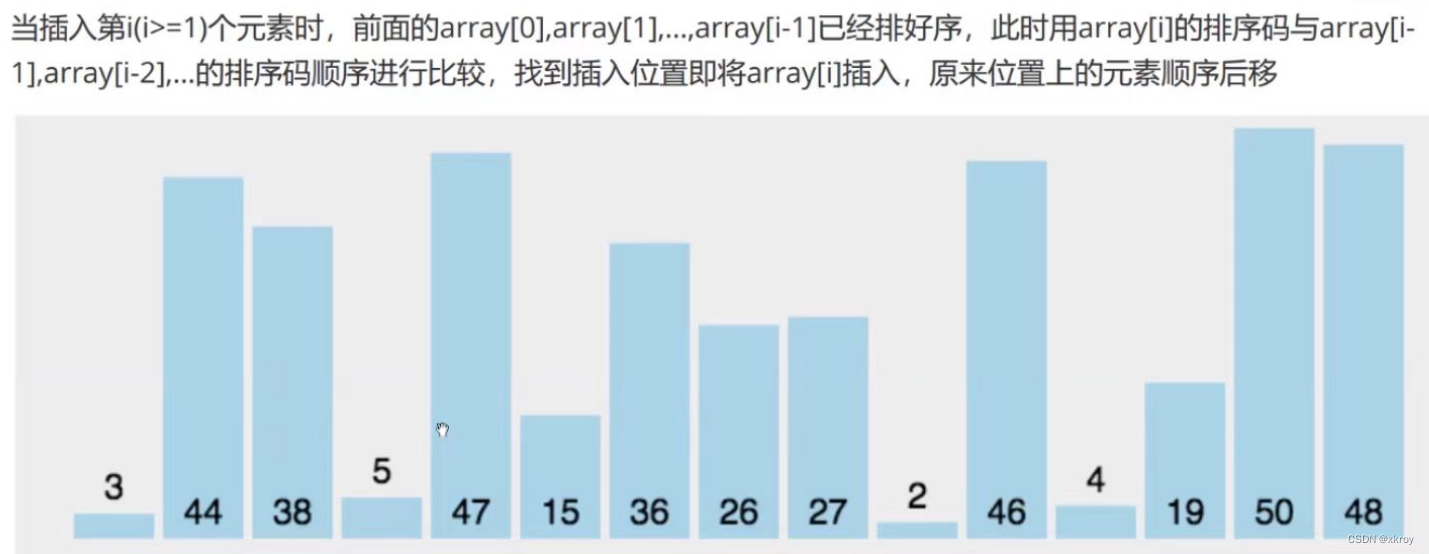
就是和前面的每一个进行比较
代码实现:
public class Sort {
public static void insertSort(int[] array) {
int i =1;
int tmp = 0;
for (; i < array.length; i++) {
tmp = array[i];
int j = i-1;
for (; j>=0; j--){
if (array[j] > tmp){
array[j+1] = array[j];
}else {
break;
}
}
array[j+1] = tmp;
}
}
}直接插入排序总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
注意:一个本身就是稳定的排序是可以实现为不稳定排序的,但一个不稳地排序无法实现稳定排序
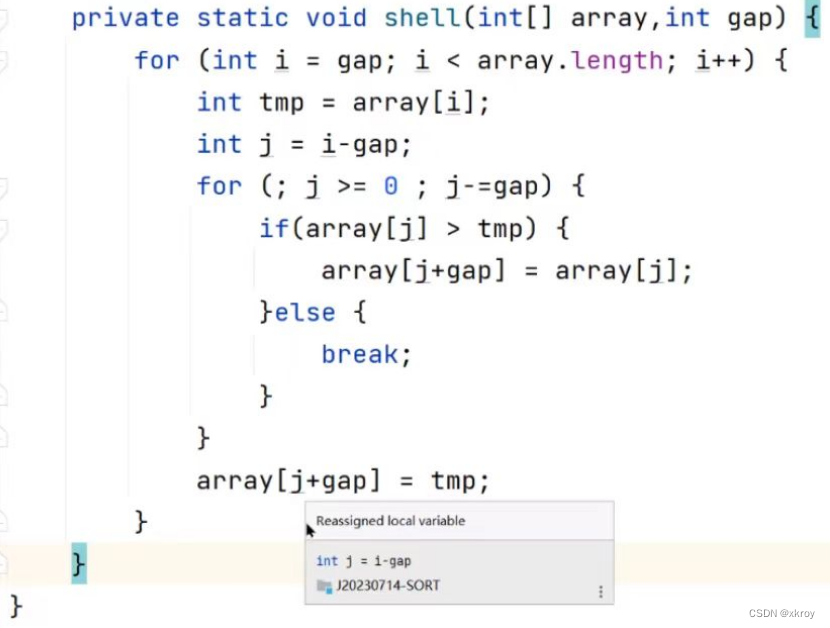
3.希尔排序(增小增量排序)

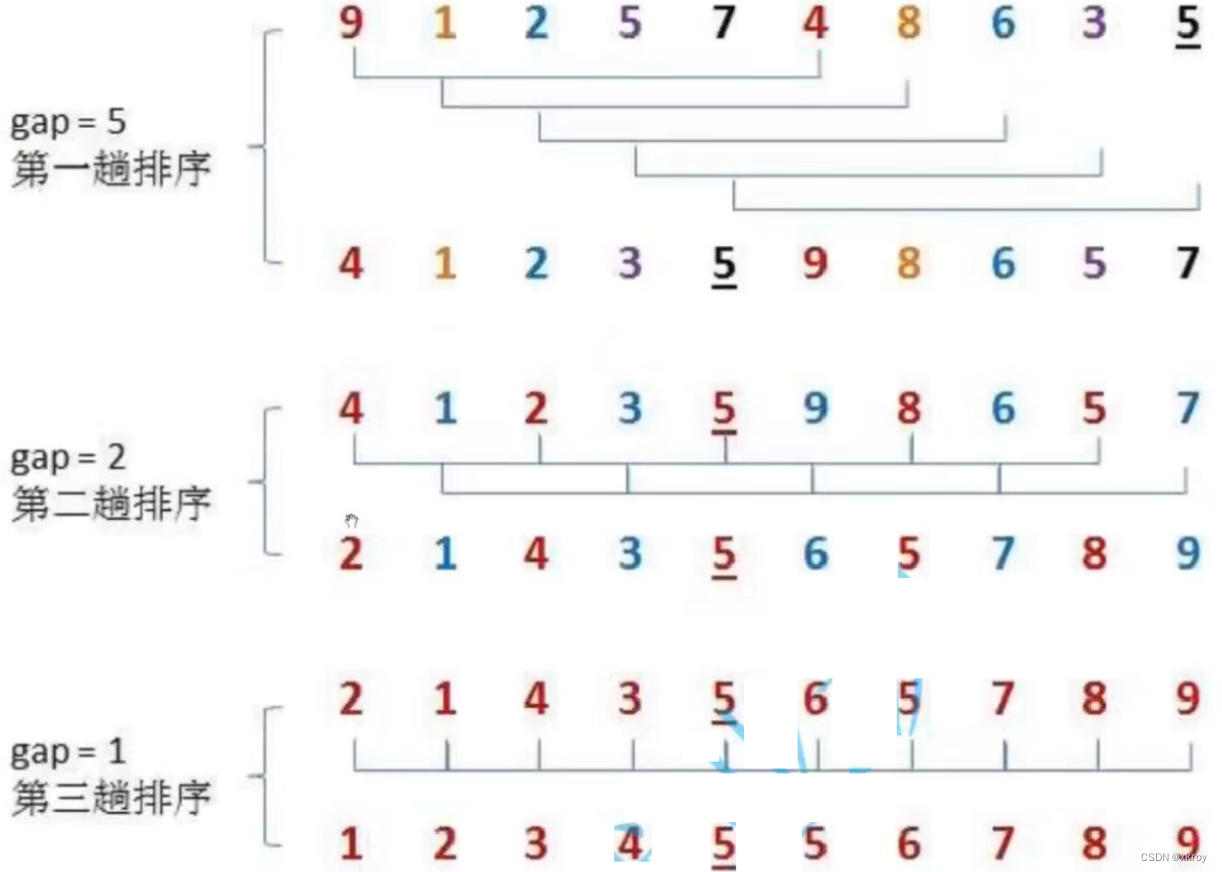
希尔排序的特性总结:

代码实现:

2.选择排序
基本思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素拍完
1.直接选择排序

代码实现:
public static void selectSort(int[] array){
for (int left = 0; left <array.length ; left++) {
int min = left;
for (int i = left+1; i < array.length; i++) {
if (array[i] < array[min]){
min = i;
}
}
int tmp = array[min];
array[min] = array[left];
array[left] = tmp;
}
}
总结:
效率较低,比较少用
时间复杂度:不管最好最坏都是:O(N^2);
空间复杂度:O(1);
稳定性:不稳定
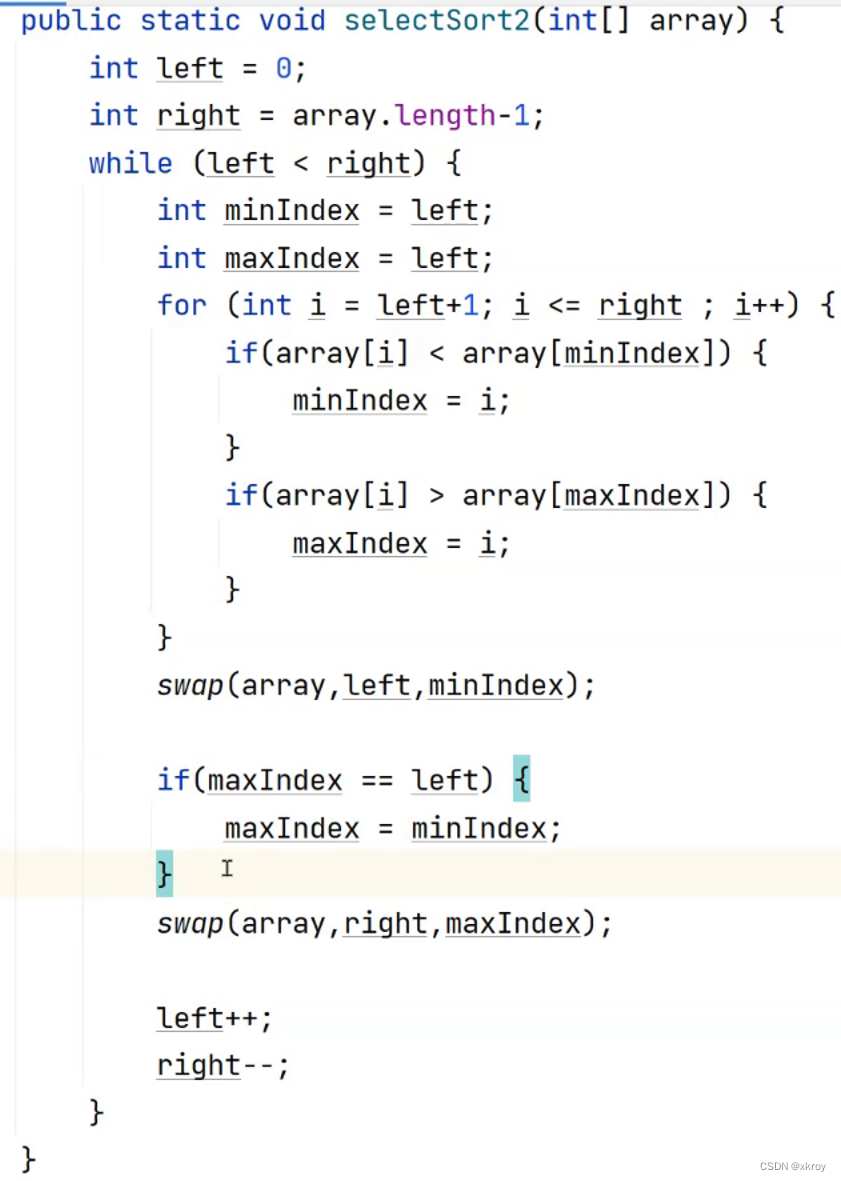
2.选择排序2
3.堆排序

public static void heapSort(int[] array){
PriorityQueue p = new PriorityQueue<Integer>(new IntCmp());
int len = array.length-1;
for (int i = 0; i < array.length; i++) {
p.offer(array[i]);
}
for (int i = 0; i < array.length; i++) {
array[i] = (int)p.poll();
}
for (int i = len; i > 0 ; i--) {
int parent = 0;
int tmp = array[i];
array[i] = array[0];
array[0] = tmp;
len--;
//向下调整
int child = (2*parent)+1;//左孩子下标
while (child < len+1) {
if(child+1 < len+1 && array[child] < array[child+1]) {
child++;
}
//child一定是 左右孩子最大值的下标
if(array[child] > array[parent]) {
tmp = array[child];
array[child] = array[parent];
array[parent] = tmp;
parent = child;
child = 2*parent+1;
}else {
//已经是大根堆了
break;
}
}
}
}
}
3.交换排序
就是根据序列中两个记录值的比较结果来对换这两个记录在序列中的位置,将值大的向序列尾部移动,较小的向序列的前部移动
1.冒泡排序
public static void bubbleSort2(int[] array){
for (int i = 0; i < array.length-1; i++) {
boolean flag = false;
for (int j = 0; j < array.length-1-i; j++) {
if (array[j] > array[j+1]){
int tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
flag = true;
}
}
if (!flag){
return;
}
}
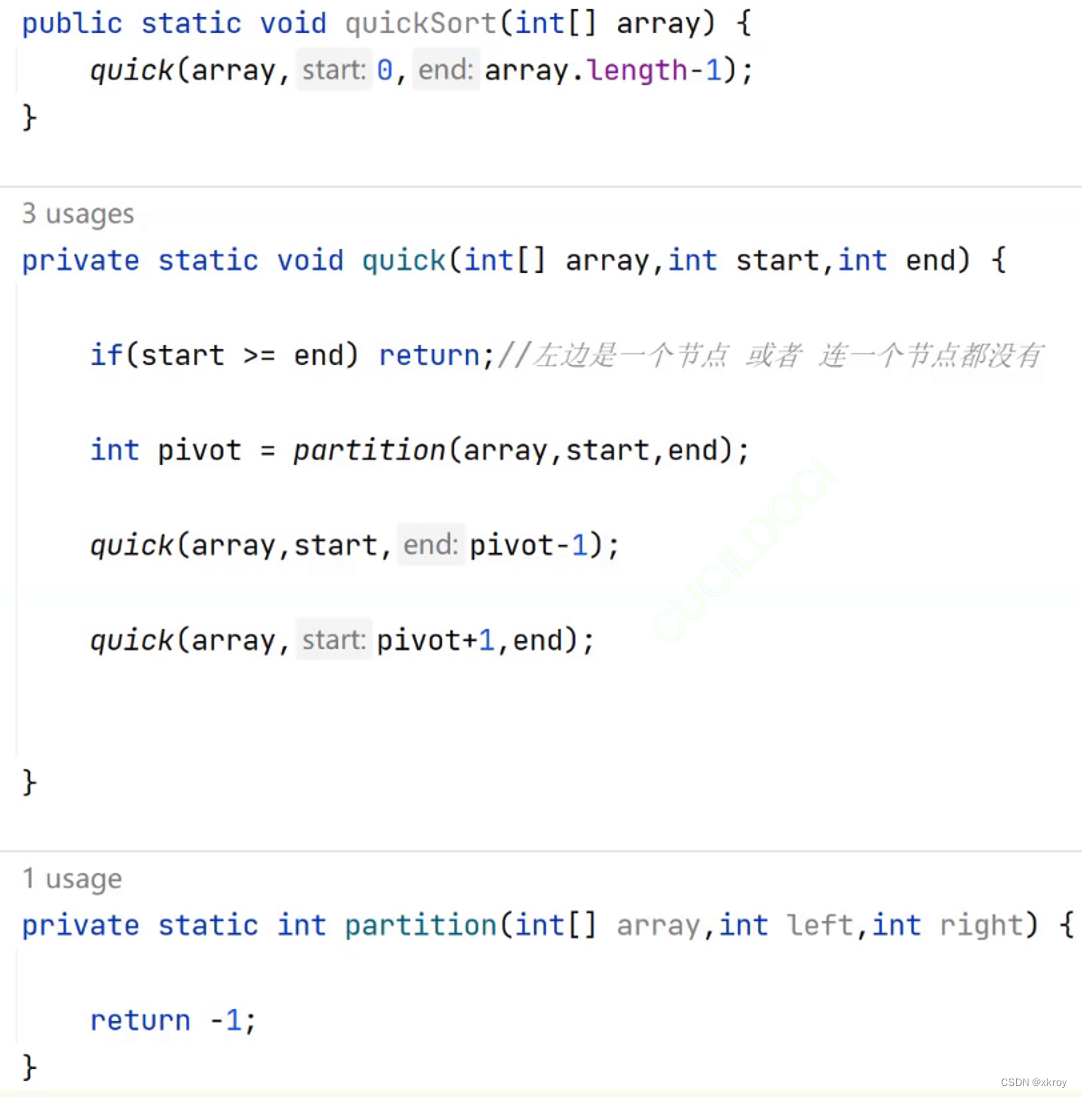
}2.快速排序
基本思想:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后左右子序列重复该过程,直到所有元素都排列在相应的位置上为止
private static void swap(int[] array,int i,int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
霍尔法:
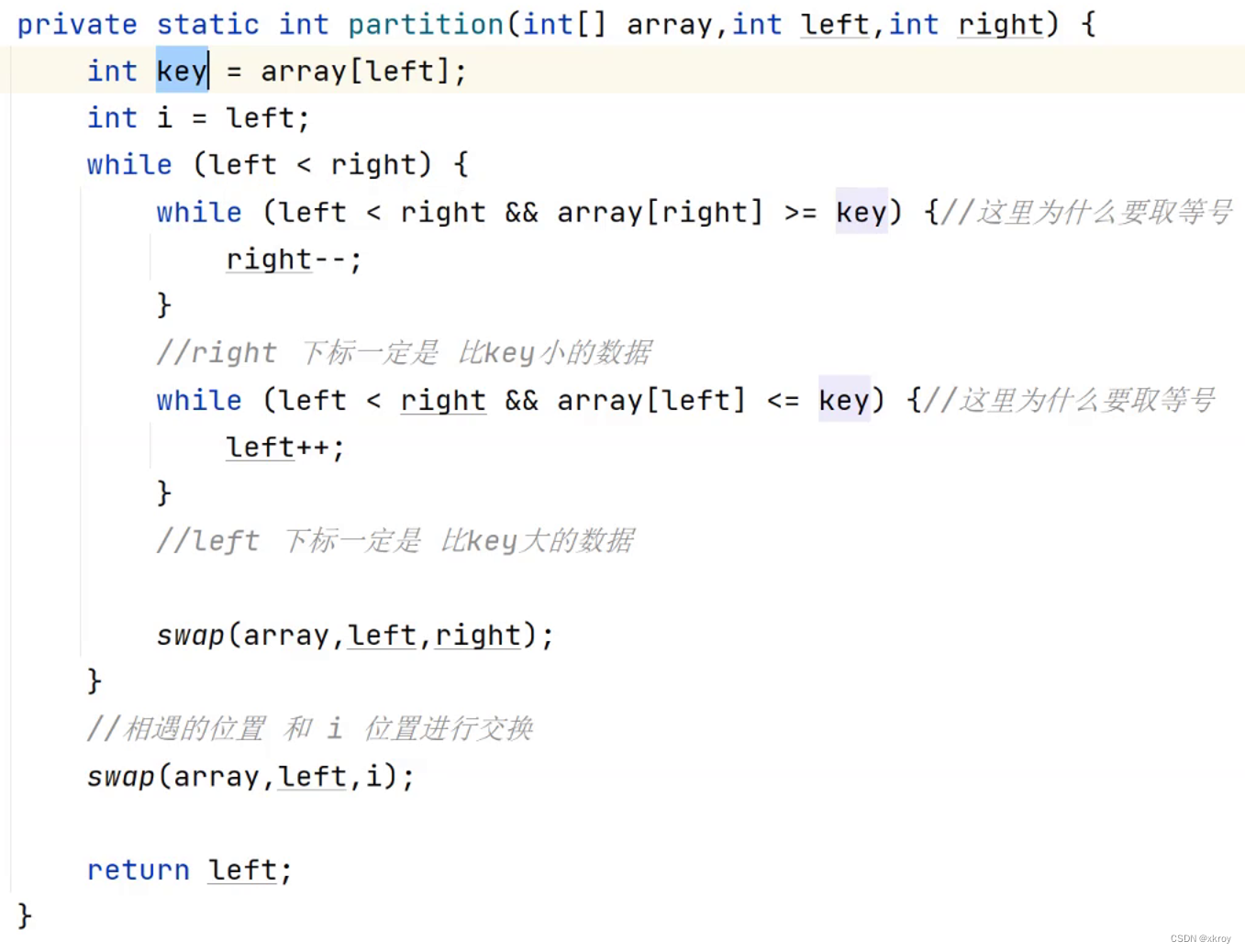
挖坑法:(主要使用)
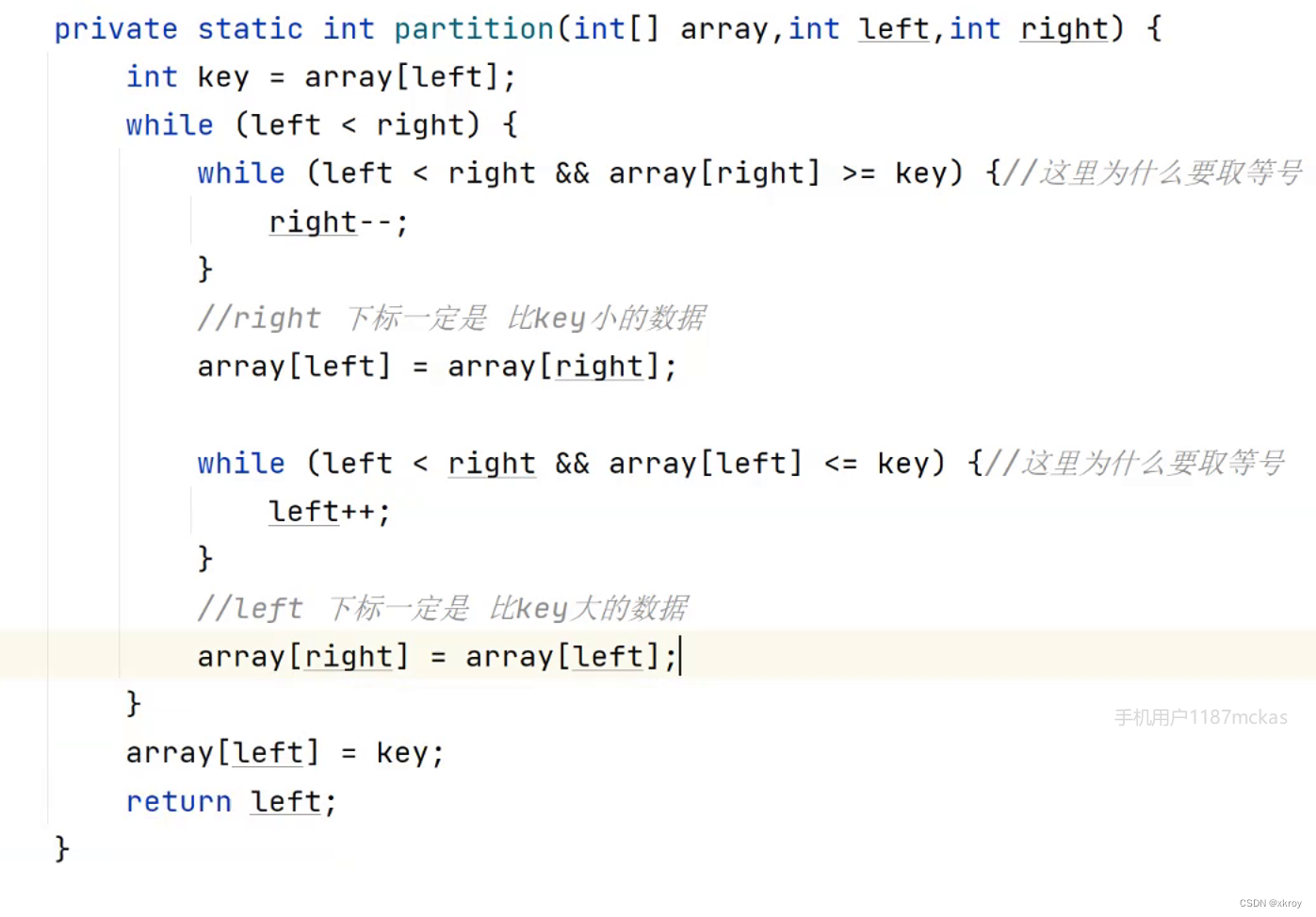
前后指针法:

3.快速排序非递归
public static void quickSortNor(int[] array) {
Stack<Integer> stack = new Stack<>();
int left = 0;
int right = array.length-1;
int piovt = partition(array,left,right);
if(piovt - 1 > left) {
stack.push(left);
stack.push(piovt-1);
}
if(piovt + 1 < right) {
stack.push(piovt+1);
stack.push(right);
}
while (!stack.isEmpty()) {
right = stack.pop();
left = stack.pop();
piovt = partition(array,left,right);
if(piovt - 1 > left) {
stack.push(left);
stack.push(piovt-1);
}
if(piovt + 1 < right) {
stack.push(piovt+1);
stack.push(right);
}
}
}
4.归并排序
归并排序是建立在归并操作上的一种有效的排序算法,采用分治法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。归并排序核心步骤:
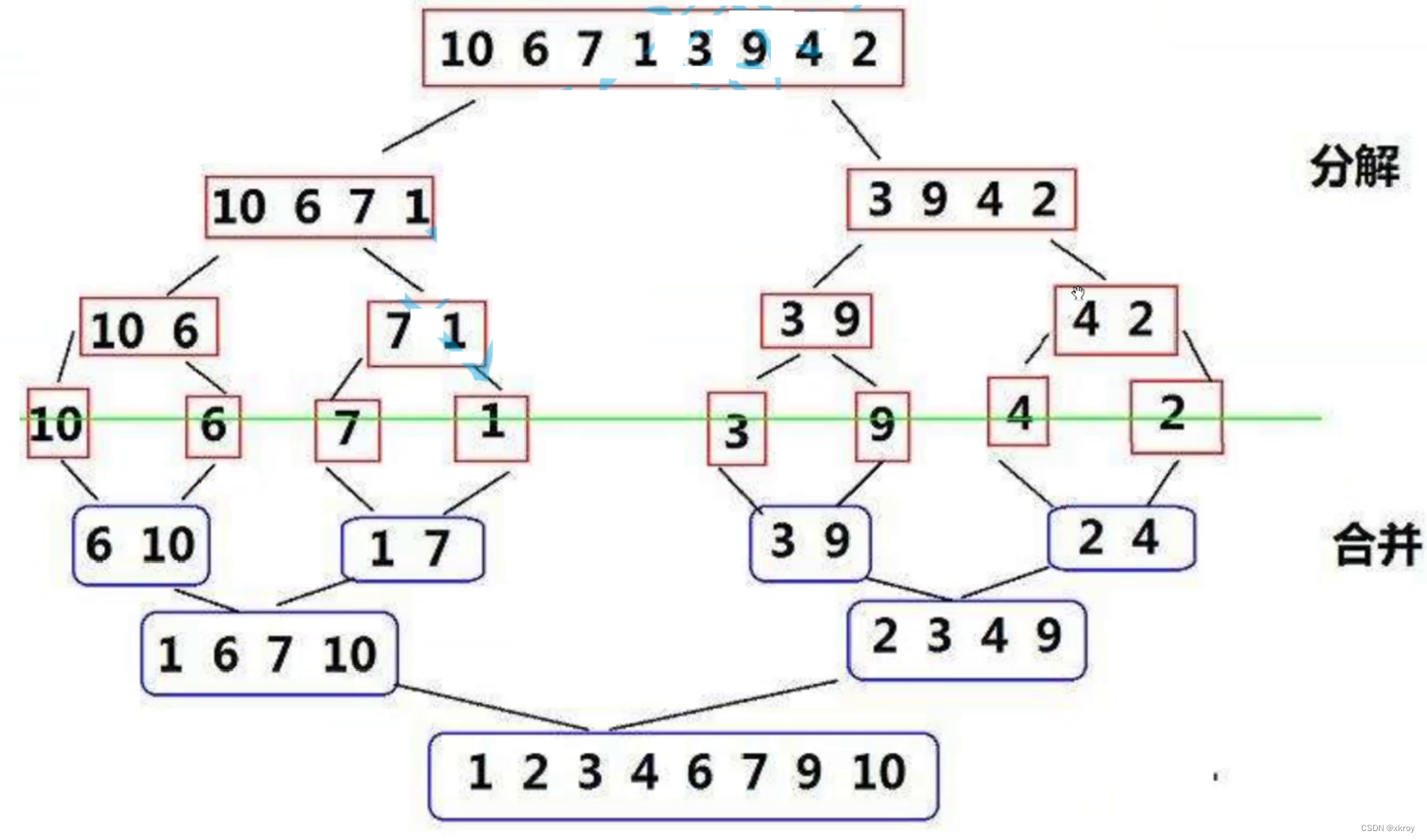
/**
* 时间复杂度: 0(N*logN)
* 空间复杂度:O(n)
* 稳定性: 稳定
* 插入排序 冒泡 归并
* @param array
*/
public static void mergeSort(int[] array) {
mergeSortFunc(array,0,array.length-1);
}
private static void mergeSortFunc(int[] array,int left,int right) {
if(left >= right) return;
int mid = (left+right) / 2;
mergeSortFunc(array,left,mid);
mergeSortFunc(array,mid+1,right);
merge(array,left,right,mid);
}
private static void merge(int[] array, int left, int right, int mid) {
int s1 = left;
int s2 = mid+1;
int[] tmpArr = new int[right-left+1];
int k = 0;
//证明两个区间 都同时有数据的
while (s1 <= mid && s2 <= right) {
if(array[s2] <= array[s1]) {
tmpArr[k++] = array[s2++];
}else {
tmpArr[k++] = array[s1++];
}
}
while (s1 <= mid) {
tmpArr[k++] = array[s1++];
}
while (s2 <= right) {
tmpArr[k++] = array[s2++];
}
//tmpArr 里面一定是这个区间内有序的数据了
for (int i = 0; i < tmpArr.length; i++) {
array[i+left] = tmpArr[i];
}
}