电路分析 ---- 加法器
1 同相加法器
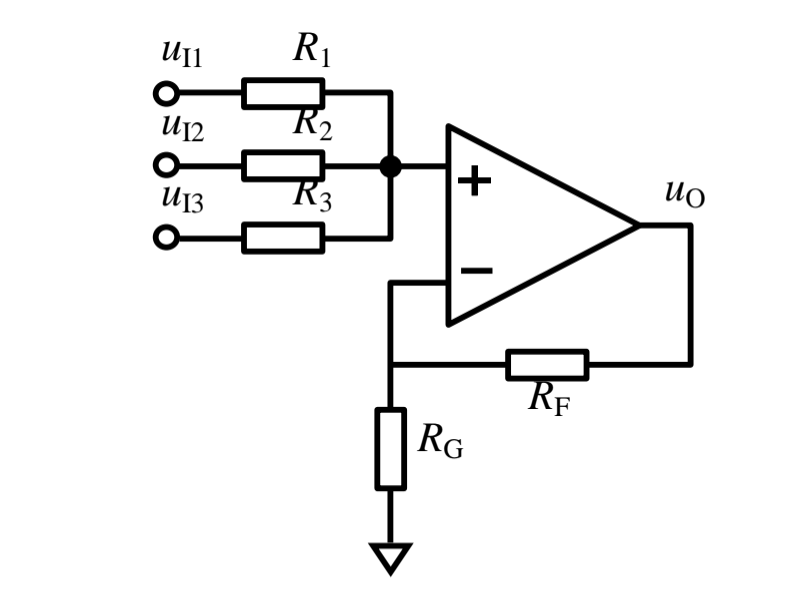
分析过程
- 虚短: u + = u − = R G R G + R F u O u_{+}=u_{-}=\cfrac{R_{G}}{R_{G}+R_{F}}u_{O} u+=u−=RG+RFRGuO
- i 1 = u I 1 − u + R 1 i_{1}=\cfrac{u_{I1}-u_{+}}{R_{1}} i1=R1uI1−u+; i 2 = u I 2 − u + R 2 i_{2}=\cfrac{u_{I2}-u_{+}}{R_{2}} i2=R2uI2−u+; i 3 = u I 3 − u + R 3 i_{3}=\cfrac{u_{I3}-u_{+}}{R_{3}} i3=R3uI3−u+;且有 i 1 + i 2 + i 3 = 0 i_{1}+i_{2}+i_{3}=0 i1+i2+i3=0.
- 所以得到 u I 1 R 1 + u I 2 R 2 + u I 3 R 3 = ( 1 R 1 + 1 R 2 + 1 R 3 ) u + \cfrac{u_{I1}}{R_{1}}+\cfrac{u_{I2}}{R_{2}}+\cfrac{u_{I3}}{R_{3}}=(\cfrac{1}{R_{1}}+\cfrac{1}{R_{2}}+\cfrac{1}{R_{3}})u_{+} R1uI1+R2uI2+R3uI3=(R11+R21+R31)u+
- 把 u + = R G R G + R F u O u_{+}=\cfrac{R_{G}}{R_{G}+R_{F}}u_{O} u+=RG+RFRGuO代入上式中,得到 u I 1 R 2 R 3 + u I 2 R 1 R 3 + u I 3 R 1 R 2 R 1 R 2 R 3 = R 2 R 3 + R 1 R 3 + R 1 R 2 R 1 R 2 R 3 ⋅ R G R G + R F ⋅ u O \cfrac{u_{I1}R_{2}R_{3}+u_{I2}R_{1}R_{3}+u_{I3}R_{1}R_{2}}{R_{1}R_{2}R_{3}}=\cfrac{R_{2}R_{3}+R_{1}R_{3}+R_{1}R_{2}}{R_{1}R_{2}R_{3}}\cdot \cfrac{R_{G}}{R_{G}+R_{F}}\cdot u_{O} R1R2R3uI1R2R3+uI2R1R3+uI3R1R2=R1R2R3R2R3+R1R3+R1R2⋅RG+RFRG⋅uO
- 变形得到 u O = ( 1 + R F R G ) u I 1 R 2 R 3 + u I 2 R 1 R 3 + u I 3 R 1 R 2 R 2 R 3 + R 1 R 3 + R 1 R 2 u_{O}=(1+\cfrac{R_{F}}{R_{G}})\cfrac{u_{I1}R_{2}R_{3}+u_{I2}R_{1}R_{3}+u_{I3}R_{1}R_{2}}{R_{2}R_{3}+R_{1}R_{3}+R_{1}R_{2}} uO=(1+RGRF)R2R3+R1R3+R1R2uI1R2R3+uI2R1R3+uI3R1R2
当三个输入电阻相等,且 R F = 2 R G R_{F}=2R_{G} RF=2RG时,此时输入输出关系为 u O = u I 1 + u I 2 + u I 3 u_{O}=u_{I1}+u_{I2}+u_{I3} uO=uI1+uI2+uI3,这时这个加法器叫等权加法器
2 反相加法器
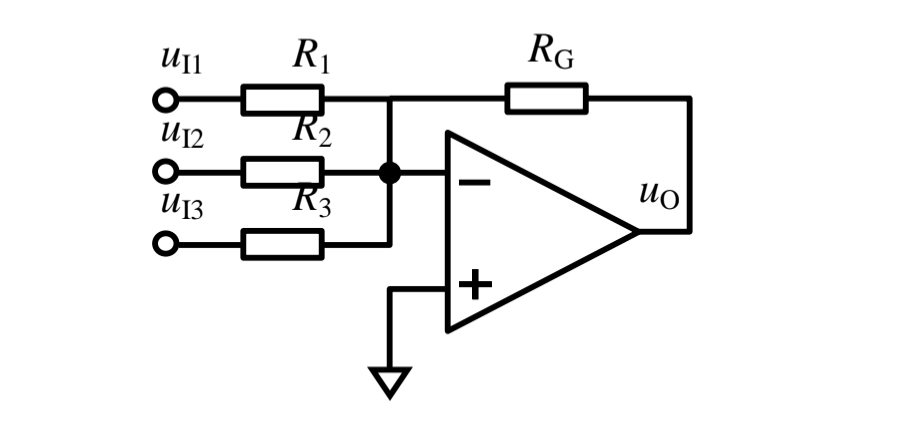
分析过程
- 虚短: u − = u + = 0 u_{-}=u_{+}=0 u−=u+=0
- i 1 = u I 1 − u − R 1 = u I 1 R 1 i_{1}=\cfrac{u_{I1}-u_{-}}{R_{1}}=\cfrac{u_{I1}}{R_{1}} i1=R1uI1−u−=R1uI1
- i 2 = u I 2 − u − R 2 = u I 2 R 2 i_{2}=\cfrac{u_{I2}-u_{-}}{R_{2}}=\cfrac{u_{I2}}{R_{2}} i2=R2uI2−u−=R2uI2
- i 3 = u I 3 − u − R 3 = u I 3 R 3 i_{3}=\cfrac{u_{I3}-u_{-}}{R_{3}}=\cfrac{u_{I3}}{R_{3}} i3=R3uI3−u−=R3uI3
- i g = u O − u − R G = u O R G i_{g}=\cfrac{u_{O}-u_{-}}{R_{G}}=\cfrac{u_{O}}{R_{G}} ig=RGuO−u−=RGuO
- 根据电流关系 i 1 + i 2 + i 3 + i g = 0 i_{1}+i_{2}+i_{3}+i_{g}=0 i1+i2+i3+ig=0
- 得到输入输出关系: u O = − ( R G R 1 u I 1 + R G R 2 u I 2 + R G R 3 u I 3 ) u_{O}=-(\cfrac{R_{G}}{R_{1}}u_{I1}+\cfrac{R_{G}}{R_{2}}u_{I2}+\cfrac{R_{G}}{R_{3}}u_{I3}) uO=−(R1RGuI1+R2RGuI2+R3RGuI3)
