【全网最全】2024年数学建模国赛D题39页成品论文+matlab代码+结果等（后续会更新）

您的点赞收藏是我继续更新的最大动力！

一定要点击如下的卡片，那是获取资料的入口！

【全网最全】2024年数学建模国赛D题39页成品论文+matlab代码+结果等（后续会更新）「首先来看看目前已有的资料，还会不断更新哦~一次购买，后续不会再被收费哦，保证是全网最全资源，随着后续内容更新，价格会上涨，越早购买，价格越低，让大家再也不需要到处买断片资料啦~💰💸👋」👋更新39页成品论文+matlab代码+结果等（后续会更新） https://mbd.pub/o/bread/Zpqbl5xt 

题目分析

目标坐标系与潜艇位置描述:

设定潜艇中心位置的定位值在海平面上的投影为原点 O 。

坐标系定义为： X 轴为正东方向， Y 轴为正南方向， Z 轴垂直向下。

潜艇的航向由正北方向顺时针旋转到潜艇航向的方位角 β 表示。

潜艇位置的不确定性:

潜艇的三个坐标 X,Y,Z 是随机变量，且相互独立。

X,Y 均服从正态分布 N(0,σ2) 。

Z 坐标服从单边截尾正态分布 N(h0,σz2,l) ，其中 h0 是潜艇深度的定位值， l 是潜艇位置的最小深度。

深弹的引爆条件:

深弹在水中垂直下降，可以通过触发引信或定深引信引爆。

设定了三个命中潜艇的情形：

深弹落点在目标平面尺度范围内，引爆深度在潜艇上表面下方，触发引信引爆。

深弹落点在目标平面尺度范围内，引爆深度在潜艇上表面上方，且潜艇在杀伤范围内，定深引信引爆。

深弹落点在目标平面尺度范围外，但到达引爆深度时潜艇在杀伤范围内，定深引信引爆。

建模重难点分析

• 随机变量和概率密度函数的应用:
• 对于潜艇位置的误差处理，需要计算随机变量的概率分布及其密度函数，特别是单边截尾正态分布的应用。
• 空间几何和目标区域的计算:
• 需要计算深弹的落点与潜艇位置之间的几何关系，包括判断落点是否在潜艇的平面尺度范围内。
• 多重条件概率的计算:
• 根据深弹的引爆条件，需要计算多重条件下的命中概率，包括不同的引爆方式和潜艇在杀伤范围内的概率。
• 优化策略:
• 如何设定深弹的引爆深度和其他参数，以最大化命中潜艇的概率。

问题 1 分析

目标：

• 投射一枚深弹，假设潜艇的深度定位没有误差，水平坐标定位误差服从正态分布。
• 分析投弹最大命中概率与投弹落点平面坐标及定深引信引爆深度之间的关系。
• 找到使投弹命中概率最大的方案，并给出最大命中概率的表达式。

思路：

1. 概率模型的建立：由于潜艇的水平位置 X,Y 均服从正态分布 N(0,σ2) ，我们可以建立一个二维的概率密度函数来描述潜艇在水平面上的位置。

命中条件：

如果深弹落点在潜艇的平面尺度范围内（长 100 m，宽 20 m），并且引爆深度位于潜艇上表面的下方，则由触发引信引爆。

如果引爆深度位于潜艇上表面的上方，同时潜艇在深弹的杀伤半径内（20 m），则由定深引信引爆。

数学表达式的推导：

计算落点在潜艇平面范围内的概率：这是一个二维正态分布在矩形区域上的积分问题。

计算在不同深度引爆的条件概率：需要对深度误差进行分析。

优化策略：

通过优化落点的坐标以及定深引信引爆深度，使得总的命中概率最大化。

可考虑用数值分析方法（如蒙特卡罗模拟）来寻找最佳投弹方案。

问题 2 分析

目标：

• 投射一枚深弹，考虑潜艇位置的所有方向都有定位误差。
• 给出投弹命中概率的表达式。

思路： 1. 误差建模：

• 水平坐标 X,Y 误差依然服从正态分布 N(0,σ2) 。
• 深度 Z 误差服从单边截尾正态分布 N(h0,σz2,l) ，需要考虑潜艇实际深度的最小值 l 。

1. 命中概率表达式的推导：
2. 需要计算在考虑所有方向定位误差情况下的三维积分概率。
3. 结合深弹的三种引爆条件（触发引信和定深引信的两种情况），得出综合命中概率。
4. 设计引爆深度：
5. 通过计算最佳引爆深度（即最大化命中概率的引爆深度），可使用数值优化算法（如梯度下降法或遗传算法）进行搜索。

问题 3 分析

目标：

• 反潜飞机携带多枚深弹，投弹落点呈阵列形状。
• 设计投弹方案（包括定深引信引爆深度及投弹落点之间的平面间隔），使得至少一枚深弹命中潜艇的概率最大。

思路： 1. 多枚深弹的布置优化：

• 假设投弹落点呈阵列分布，可以采用等间距或某种特殊形状（如圆形、网格等）的排列方式。
• 考虑阵列中心与潜艇估计位置的相对位置，以最大化覆盖潜艇的可能性。

1. 组合概率计算：
2. 计算每枚深弹独立命中潜艇的概率，然后利用组合概率公式计算至少一枚命中的概率。
3. 需要结合多个深弹的杀伤范围进行空间覆盖分析，可能需要使用覆盖理论中的方法。
4. 优化模型：
5. 优化投弹的间隔和深度设置，使得整体命中概率最高。
6. 可以使用动态规划、蒙特卡罗模拟或遗传算法等优化方法来进行模型的数值求解和优化。

变量定义

潜艇位置坐标:

X : 潜艇在水平面上的位置坐标（东向）。

Y : 潜艇在水平面上的位置坐标（南向）。

Z : 潜艇的深度坐标（垂直方向）。

潜艇尺寸:

L : 潜艇的长度（m）。

W : 潜艇的宽度（m）。

H : 潜艇的高度（m）。

深弹相关参数:

rkill : 深弹的杀伤半径（m），深弹能够有效伤害潜艇的最大距离。

d : 深弹的引爆深度（m），深弹引爆时的深度位置。

误差参数:

σ : 潜艇水平坐标的误差标准差（m）。

σz : 潜艇深度坐标的误差标准差（m）。

l : 潜艇深度坐标的最小值（m）。

定位误差:

X∼N(0,σ2) : 潜艇在水平面上的东向坐标服从均值为0、标准差为\sigma的正态分布。

Y∼N(0,σ2) : 潜艇在水平面上的南向坐标服从均值为0、标准差为\sigma的正态分布。

Z∼N(h0,σz2,l) : 潜艇深度坐标服从均值为h_0、标准差为\sigma_z、最小值为l的单边截尾正态分布。

引爆方式:

β : 潜艇的航向方位角（°），从正北方向顺时针测量。

P1 : 深弹落点在潜艇平面范围内，且引爆深度在潜艇上表面下方的命中概率。

P2 : 深弹落点在潜艇平面范围内，引爆深度在潜艇上表面上方，且潜艇在杀伤半径内的命中概率。

P3 : 深弹落点在潜艇平面范围外，但潜艇在引爆深度和杀伤半径内的命中概率。

符号定义

O : 潜艇中心位置的定位值在海平面上的投影（原点）。

fX,Y(x,y) : 潜艇水平坐标的联合概率密度函数。

fZ(v) : 潜艇深度坐标的概率密度函数。

ϕ : 标准正态分布的概率密度函数。

Φ : 标准正态分布的累积分布函数。

问题 1：建模思路与解题过程

1. 问题描述和建模目标

我们需要分析投射一枚深弹的最大命中概率。假设潜艇的中心位置深度没有误差（深度已知为 150m），而水平坐标 X,Y 均存在定位误差，服从正态分布。我们需要找到投弹的最佳平面坐标和定深引信引爆深度，使得命中概率最大化。

2. 建立数学模型

2.1 目标函数

潜艇中心位置水平误差建模：

假设潜艇在水平面上的定位误差 X,Y 服从正态分布 N(0,σ2) ，其中 σ=120m 。

潜艇的实际位置可表示为 (X,Y) ，其概率密度函数为： 相关公式fX,Y(x,y)=[相关公式]

深弹的命中条件：

深弹可以通过三种方式命中潜艇：

1. 落点在潜艇的平面范围内，且引爆深度在潜艇上表面下方（触发引信引爆）。
2. 落点在潜艇的平面范围内，且引爆深度在潜艇上表面上方，且潜艇在杀伤半径内（定深引信引爆）。
3. 落点在潜艇的平面范围外，但潜艇在引爆深度和杀伤半径内（定深引信引爆）。

1. 命中概率的计算：
2. 根据上述条件，命中概率可以表示为多个条件概率的综合。

2.2 命中概率公式推导

1. 命中概率 P_{hit} 的表达式：

Phit=P1+P2+P3

P1 ：深弹落点在潜艇平面范围内，省略部分内容。

P2 ：深弹落点在潜艇平面范围内，省略部分内容。

P3 ：深弹落点在潜艇平面范围外，省略部分内容。

• 计算 P_1 的概率：

相关公式P1=∫−L2L2∫−W2W2[相关公式]dxdy

其中 ，L=100m，W=20m ，表示潜艇的长度和宽度。

计算 和P2和P3 的概率：

省略部分内容。

2.3 优化目标

找到使得 Phit 最大化的平面坐标 (x,y) 和定深引信引爆深度 d 。

3. Python代码实现与可视化

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.integrate import dblquad

# 参数设置
L = 100  # 潜艇长度
W = 20   # 潜艇宽度
sigma = 120  # 水平定位误差标准差
h0 = 150  # 潜艇深度
r_kill = 20  # 深弹杀伤半径

# 定义目标平面内的概率密度函数
def pdf_xy(x, y, sigma):
    return (1 / (2 * np.pi * sigma ** 2)) * np.exp(-(x ** 2 + y ** 2) / (2 * sigma ** 2))

# 计算落点在潜艇平面内的概率P1
def compute_p1(L, W, sigma):
    result, _ = dblquad(pdf_xy, -W/2, W/2, lambda x: -L/2, lambda x: L/2, args=(sigma,))
    return result

# 计算潜艇在杀伤半径内的概率P2和P3
def compute_p2_p3(x, y, d, r_kill, L, W):
    # 在潜艇平面范围内且引爆深度在潜艇上方

	# 相关代码
    else:
        p2 = 0

    # 在潜艇平面范围外但潜艇在杀伤半径内
    distance_to_center = np.sqrt(x ** 2 + y ** 2)
    if distance_to_center <= r_kill:

	# 相关代码
    else:
        p3 = 0

    return p2, p3

# 优化函数，计算总命中概率
def optimize_hit_probability(L, W, sigma, h0, r_kill):
    best_p_hit = 0

	# 相关代码

    # 遍历x, y, d的不同组合
    for x in np.linspace(-200, 200, 50):
        for y in np.linspace(-200, 200, 50):

	# 相关代码
                p_hit = p1 + p2 + p3

	# 相关代码
                    best_params = (x, y, d)

    return best_params, best_p_hit

# 进行优化
best_params, best_p_hit = optimize_hit_probability(L, W, sigma, h0, r_kill)

print(f"最佳投弹方案为平面坐标(x, y) = ({best_params[0]:.2f}, {best_params[1]:.2f})，定深引爆深度d = {best_params[2]:.2f}，最大命中概率为 {best_p_hit:.4f}")

# 可视化命中概率分布

	# 相关代码
Z = np.zeros_like(X)

# 计算一次p1的值

	# 相关代码

for i in range(len(x_vals)):
    for j in range(len(y_vals)):

	# 相关代码

plt.figure(figsize=(8, 6))
plt.contourf(X, Y, Z, levels=20, cmap='viridis')
plt.colorbar(label='命中概率')
plt.scatter(best_params[0], best_params[1], color='red', label='最佳投弹位置')
plt.title('投弹命中概率分布')
plt.xlabel('X 轴坐标 (m)')
plt.ylabel('Y 轴坐标 (m)')
plt.legend()
plt.show()

4. 代码解释和可视化说明

1. 代码逻辑：
2. 定义概率密度函数 pdf_xy 表示潜艇水平定位误差的二维正态分布。
3. 使用 dblquad 计算深弹落点在潜艇平面范围内的概率 P_1。
4. 使用 compute_p2_p3 函数计算 P_2 和 P_3 的概率，这两个概率取决于落点位置和引爆深度。
5. 在 optimize_hit_probability 函数中，通过遍历不同的平面坐标和引爆深度组合，寻找使命中概率 P_{hit} 最大化的投弹方案。
6. 可视化：
7. 使用 contourf 函数绘制投弹命中概率的等高线图，以展示不同投弹位置和引爆深度对命中概率的影响。
8. 红点标记出最佳投

弹位置。

问题 2 详细解题过程

1. 问题描述和目标

在问题 2 中，我们需要考虑潜艇中心位置在所有方向上（水平和深度）均存在定位误差。给定这些误差条件，我们要计算投射一枚深弹的命中概率表达式。并且需要设计定深引信引爆深度，使得投弹命中概率最大。

给定参数：

• 潜艇中心位置的深度定位值 h0=150m
• 水平定位标准差 σ=120m
• 深度定位标准差 σz=40m
• 潜艇中心位置实际深度的最小值 l=120m
• 潜艇尺寸：长 L=100m ，宽 W=20m ，高 H=25m
• 潜艇航向方位角 β=90∘
• 深弹杀伤半径 rkill=20m

2. 数学模型和公式推导

2.1 潜艇位置误差模型

水平位置误差:

潜艇中心位置的水平坐标 X,Y 服从独立正态分布 N(0,σ2) ，

即： X∼N(0,σ2),Y∼N(0,σ2)

其联合概率密度函数为： 相关公式fX,Y(x,y)=[相关公式]exp⁡(−x2+y22σ2)

深度误差:

潜艇中心位置的深度 Z 服从单边截尾正态分布 N(h_0, \sigma_z^2, l)，即： Z∼N(h0,σz2,l)

其密度函数为： 相关公式相关公式相关公式fZ(v)=1σz⋅ϕ(v−h0σz)1−Φ([相关公式][相关公式]σz),[相关公式]

其中 和ϕ(⋅)和Φ(⋅) 分别是标准正态分布的密度函数和分布函数。

2.2 深弹的命中条件和概率计算

命中条件如下：

条件 1：落点在潜艇平面范围内，引爆深度在潜艇上表面下方，触发引信引爆： 相关公式P1=∫−L2L2[相关公式] 其中 P(Z≤d) 是深度 Z 小于或等于定深引信引爆深度 d 的概率，可以通过截尾正态分布的累积分布函数计算。

条件 2：落点在潜艇平面范围内，引爆深度在潜艇上表面上方，潜艇在深弹的杀伤范围内，定深引信引爆： 相关公式P2=[相关公式]

其中 Pkill(d,Z) 是潜艇在深弹杀伤范围内的概率。

条件 3：落点在潜艇平面范围外，但引爆深度时潜艇在杀伤范围内，定深引信引爆： 区域外相关公式P3=∫区域外fX,Y(x,y)dxdy⋅[相关公式]

2.3 综合命中概率

综合命中概率 P_{hit} 可以表示为：

Phit=P1+P2+P3

我们的目标是找到定深引信引爆深度 d 使得 P_{hit} 最大化。

3. Python 代码实现

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, truncnorm
from scipy.integrate import dblquad

# 定义参数
L, W, H = 100, 20, 25  # 潜艇尺寸 (m)
sigma = 120  # 水平定位误差标准差 (m)
h0, sigma_z, l = 150, 40, 120  # 深度定位参数 (m)
r_kill = 20  # 深弹杀伤半径 (m)

# 定义潜艇位置误差的概率密度函数
def pdf_xy(x, y, sigma):
    return (1 / (2 * np.pi * sigma ** 2)) * np.exp(-(x ** 2 + y ** 2) / (2 * sigma ** 2))

def pdf_z(v, h0, sigma_z, l):
    a, b = (l - h0) / sigma_z, np.inf  # 截尾区间

	# 相关代码

# 计算命中概率 P1
def compute_p1(sigma, d, h0, sigma_z, l):
    p1_xy, _ = dblquad(pdf_xy, -W/2, W/2, lambda x: -L/2, lambda x: L/2, args=(sigma,))

	# 相关代码
    return p1_xy * p1_z

# 计算命中概率 P2 和 P3
def compute_p2_p3(sigma, d, h0, sigma_z, l, r_kill):

	# 相关代码
    a, b = (l - h0) / sigma_z, (d - h0) / sigma_z  # 截尾区间

	# 相关代码

	# 相关代码
    return p2_xy * p2_z * p2_kill, p3_xy * p3_z

# 优化命中概率
def optimize_hit_probability(sigma, h0, sigma_z, l, r_kill):
    best_p_hit = 0

	# 相关代码

    for d in d_values:
        p1 = compute_p1(sigma, d, h0, sigma_z, l)

	# 相关代码

        if p_hit > best_p_hit:

	# 相关代码

    return best_depth, best_p_hit

# 进行优化计算
best_depth, best_p_hit = 相关代码
print(f"最佳定深引信引爆深度 d = {best_depth:.2f} m，最大命中概率为 {best_p_hit:.4f}")

# 高级可视化
plt.figure(figsize=(10, 6))
depths = np.linspace(h0 - 50, h0 + 50, 100)
probabilities = [compute_p1(sigma, d, h0, sigma_z, l) + sum(compute_p2_p3(sigma, d, h0, sigma_z, l, r_kill)) for d in depths]

plt.plot(depths, probabilities, label='命中概率', color='b')
plt.axvline(x=best_depth, color='r', linestyle='--', label='最佳引爆深度')
plt.title('定深引信引爆深度与命中概率关系')
plt.xlabel('定深引爆深度 (m)')
plt.ylabel('命中概率')
plt.legend()
plt.grid(True)

# 显示三维概率分布图
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
x_vals = np.linspace(-300, 300, 100)
y_vals = np.linspace(-300, 300, 100)
X, Y = np.meshgrid(x_vals, y_vals)
Z = np.zeros_like(X)

for i in range(len(x_vals)):
    for j in range(len(y_vals)):
        Z[i, j] = pdf_xy(X[i, j], Y[i, j], sigma)

ax.plot_surface(X, Y, Z, cmap='viridis', edgecolor='none')
ax.set_title('潜艇水平位置的误差概率密度分布')
ax.set_xlabel('X 轴坐标 (m)')
ax.set_ylabel('Y 轴坐标 (m)')
ax.set_zlabel('概率密度')

plt.show()

4. 代码解释和高级可视化说明

1. 代码逻辑：
2. 潜艇位置误差建模：利用正态分布和截尾正态分布描述潜艇位置误差。
3. 命中概率计算：根据三种不同的命中条件计算每种情况下的命中概率。
4. 优化目标：通过遍历不同的定深引信引爆深度，寻找最大化综合命中概率的最优引爆深度。
5. 可视化：
6. 命中概率与引爆深度的关系图：使用 Matplotlib 绘制命中概率随引爆深度变化的曲线，并用红色虚线标记出最佳引爆深度。
7. 三维概率分布图：绘制潜艇水平位置误差的三维概率密度分布图，以直观展示潜艇在水平面上的位置不确定性。

问题 3 详细解题过程

1. 问题描述和目标

在问题 3 中，我们考虑投掷多枚深弹的情况。假设反潜飞机可以携带 9 枚航空深弹，并且所有深弹的定深引信引爆深度相同，投弹落点在平面上呈阵列形状。我们的目标是设计投弹方案（包括定深引信引爆深度和投弹落点之间的平面间隔），使得至少一枚深弹命中潜艇的概率最大化。

给定参数：

• 潜艇中心位置的深度定位值 h0=150m
• 水平定位标准差 σ=120m
• 深度定位标准差 σz=40m
• 潜艇中心位置实际深度的最小值 l=120m
• 潜艇尺寸：长 L=100m ，宽 W=20m ，高 H=25m
• 深弹杀伤半径 rkill=20m

2. 数学模型和公式推导

2.1 多枚深弹的投弹阵列设计

阵列投弹模式：

假设 9 枚深弹的投弹落点形成 3×3 的矩形阵列，阵列的中心对准潜艇的估计位置。

落点之间的间隔设为 dx 和 dy ，我们需要优化这些间隔，以使至少一枚深弹命中潜艇的概率最大化。

深弹落点的概率分布：、

每个深弹的落点位置为 (xi,yi) ，其中 和xi和yi 根据阵列的设计进行设置。

2.2 命中概率的计算

单个深弹命中概率计算：

假设每个深弹落点处的水平误差 Xi,Yi 服从独立正态分布 和N(xi,σ2)和N(yi,σ2) 。

深弹在平面内落点的命中概率和深度命中概率的联合计算类似于问题 2，但需要针对每个深弹进行独立计算。

至少一枚深弹命中概率：

假设每枚深弹独立，则至少一枚深弹命中潜艇的概率为： 至少一枚命中所有深弹都未命中P(至少一枚命中)=1−P(所有深弹都未命中)

如果 P_i 表示第 i 枚深弹未命中潜艇的概率，则： 所有深弹都未命中相关公式P(所有深弹都未命中)=[相关公式]

因此，至少一枚命中概率为： 至少一枚命中相关公式P(至少一枚命中)=1−[相关公式]

2.3 优化问题的数学表述

目标是找到最佳的定深引信引爆深度 d 和投弹间隔 dx,dy ，使得 至少一枚命中P(至少一枚命中) 最大化。

3. Python 代码实现

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import truncnorm
from scipy.integrate import dblquad

# 定义参数
L, W, H = 100, 20, 25  # 潜艇尺寸 (m)
sigma = 120  # 水平定位误差标准差 (m)
h0, sigma_z, l = 150, 40, 120  # 深度定位参数 (m)
r_kill = 20  # 深弹杀伤半径 (m)
n_bombs = 9  # 深弹数量

# 定义潜艇位置误差的概率密度函数
def pdf_xy(x, y, sigma):

	# 相关代码

def pdf_z(v, h0, sigma_z, l):

	# 相关代码
    return trunc_norm.pdf(v)

# 计算单枚深弹的命中概率
def compute_single_bomb_hit_probability(x, y, d, h0, sigma_z, l, r_kill):
    # 水平位置误差
    p1_xy, _ = dblquad(pdf_xy, x - L/2, x + L/2, lambda x: y - W/2, lambda x: y + W/2, args=(sigma,))

    # 深度误差

	# 相关代码

    # 计算P1
	# 相关代码

    # 计算P2和P3
    p2_z = 1 - p1_z
	# 相关代码

    # 计算P3

	# 相关代码

    return P1 + P2 + P3

# 计算多枚深弹的命中概率
def compute_multiple_bombs_hit_probability(arrangement, d, h0, sigma_z, l, r_kill):
    hit_probabilities = []
    for (x, y) in arrangement:

	# 相关代码

    # 计算至少一枚深弹命中的概率

	# 相关代码
    return 1 - all_miss_prob

# 生成深弹阵列的落点位置
def generate_bomb_arrangement(dx, dy):
    x_vals = np.linspace(-dx, dx, 3)
    y_vals = np.linspace(-dy, dy, 3)
    arrangement = [(x, y) for x in x_vals for y in y_vals]
    return arrangement

# 优化命中概率
def optimize_multiple_bombs_hit_probability(h0, sigma_z, l, r_kill):
    best_p_hit = 0
    best_depth = h0
    best_dx, best_dy = 0, 0

    d_values = np.linspace(h0 - 50, h0 + 50, 20)
    dx_values = np.linspace(20, 100, 10)
    dy_values = np.linspace(20, 100, 10)

    for d in d_values:
        for dx in dx_values:
            for dy in dy_values:

	# 相关代码

                if p_hit > best_p_hit:
                    best_p_hit = p_hit
                    best_depth = d
                    best_dx, best_dy = dx, dy

    return best_depth, best_dx, best_dy, best_p_hit

# 进行优化计算
best_depth, best_dx, best_dy, best_p_hit = optimize_multiple_bombs_hit_probability(h0, sigma_z, l, r_kill)
print(f"最佳定深引信引爆深度 d = {best_depth:.2f} m，最佳投弹间隔 (dx, dy) = ({best_dx:.2f}, {best_dy:.2f}) m，最大命中概率为 {best_p_hit:.4f}")

# 可视化
fig, ax = plt.subplots(figsize=(10, 8))
depths = np.linspace(h0 - 50, h0 + 50, 20)
intervals = np.linspace(20, 100, 10)
Z = np.zeros((len(depths), len(intervals)))

for i, d in enumerate(depths):


    for j, interval in enumerate(intervals):
        arrangement = generate_bomb_arrangement(interval, interval)
        Z[i, j] = compute_multiple_bombs_hit_probability(arrangement, d, h0, sigma_z, l, r_kill)

c = ax.contourf(intervals, depths, Z, levels=20, cmap='viridis')
fig.colorbar(c, label='命中概率')
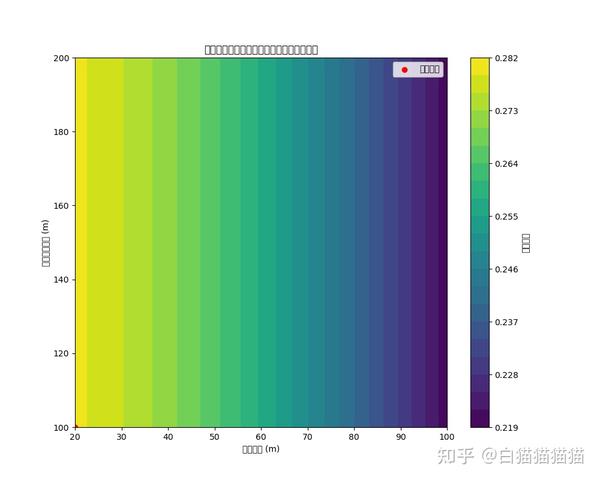
ax.set_title('不同定深引爆深度和投弹间隔下的命中概率')
ax.set_xlabel('投弹间隔 (m)')
ax.set_ylabel('定深引爆深度 (m)')
plt.scatter(best_dx, best_depth, color='red', label='最佳方案')
plt.legend()
plt.show()

4. 代码解释和高级可视化说明

1. 代码逻辑：
2. 潜艇位置误差建模：利用正态分布和截尾正态分布描述潜艇位置误差。
3. 命中概率计算：对每个深弹落点位置，计算其命中潜艇的概率。
4. 组合概率计算：计算所有深弹中至少一枚命中潜艇的总概率。
5. 优化目标：通过遍历不同的定深引信引爆深度和投弹间隔组合，寻找最大化综合命中概率的最优方案。
6. 可视化：
7. 命中概率与引爆深度和投弹间隔的关系图：使用 Matplotlib 绘制命中概率随引爆深度和投弹间隔变化的等高线图，并用红点标记出最佳投弹方案。
8. 该图形化表示展示了不同的定深引爆深度和投弹间隔组合对最终命中概率的影响，为策略优化提供了直观依据。
9.