2024全国大学省数学建模竞赛A题-原创参考论文(部分+第一问代码)
一问题重述
1.1 问题背景
"板凳龙",又称"盘龙",是浙闽地区的传统地方民俗文化活动。这种独特的表演艺术形式融合了中国传统龙舞的精髓和地方特色,展现了人们对美好生活的向往和对传统文化的传承。
在板凳龙表演中,人们将少则几十条,多则上百条的板凳首尾相连,形成蜿蜒曲折的"龙"形。这种创新的表演方式不仅展现了民间艺术的智慧,也体现了集体协作的精神。盘龙时,龙头在前领头,龙身和龙尾相随盘旋,整体呈现出一种动态的圆盘状态,给观众带来视觉上的震撼和美感享受。
板凳龙的表演质量主要体现在其运动的协调性和观赏性上。一般来说,在舞龙队能够自如地盘入和盘出的前提下,盘龙所需要的面积越小、行进速度越快,则观赏性越好。这就要求表演者们必须具备高超的技巧和默契的配合。
1.2 问题要求
板凳龙是一种独特的民间艺术表演形式,由大量板凳连接而成,模仿传统舞龙的动态美感。表演时,参与者通过精妙的配合,使板凳龙呈现出蜿蜒曲折、盘旋起伏的动态。问题给出了板凳龙的构成要素,包括龙头、龙身和龙尾的具体数量和尺寸,描述了板凳之间的连接方式,并提供了表演场地的形状与尺寸。同时,问题建立了表演场地的坐标系统,用于精确描述板凳龙的运动轨迹。此外,问题还给出了龙头速度、运动轨迹等参数的具体取值,对板凳的摆放位置、连接方式等技术细节作出了明确规定,并给出了"表演完整度"指标的具体计算方法。问题中还详细说明了板凳龙的初始位置、运动方向,以及表演时间等关键信息,为后续的数学建模和分析提供了必要的基础数据。基于以上背景信息,现要求我们解决如下三个问题:
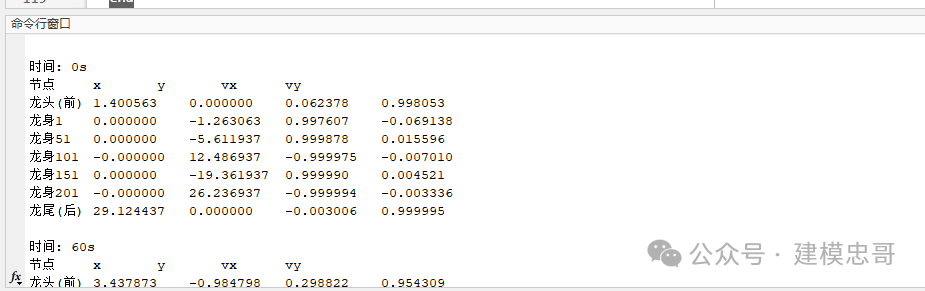
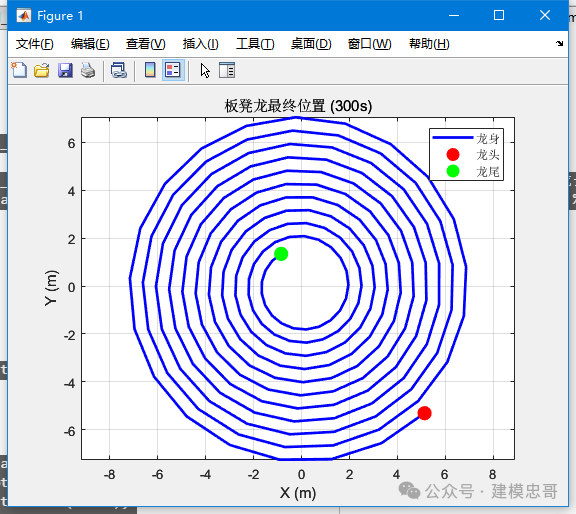
问题一:我们需要建立数学模型来描述和分析板凳龙的运动过程。其中舞龙队沿螺距为55 cm的等距螺线顺时针盘入,各把手中心均位于螺线上。龙头前把手的行进速度始终保持1 m/s。初始时,龙头位于螺线第16圈A点处。我们需要计算从初始时刻到300秒为止,每秒整个舞龙队的位置和速度。这里的位置和速度指的是龙头、龙身和龙尾各前把手及龙尾后把手中心的位置和速度。计算结果需要保存到文件result1.xlsx中。结果应保留6位小数。在论文中,我们还需要给出0 s、60 s、120 s、180 s、240 s、300 s这几个特定时刻,龙头前把手、龙头后面第1、51、101、151、201节龙身前把手和龙尾后把手的位置和速度。
问题二:它指出板凳龙的最大盘入半径为30米。在各板凳长度、宽度相同的条件下,问题要求我们确定舞龙队盘入的终止时刻,使得板凳之间不发生碰撞(即舞龙队不能再继续盘入的时间)。要求我们计算此时舞龙队的位置和速度,并按照指定格式将结果存放到文件result2.xlsx中(模板文件见附件)。同时在论文中给出此时龙头前把手、龙头后面第1、51、101、151、201条龙身前把手和龙尾后把手的位置和速度。此外,还需要分析终止盘入的原因,并讨论如何优化板凳龙的设计以延长盘入时间。要求我们按照指定格式将计算结果写入表1,将各板凳的最终位置和速度数据写入附件result2.xlsx中。
问题三:它指出舞龙队需要在一个特定的调头空间内完成从顺时针盘入到逆时针盘出的转换。调头空间被定义为以螺线中心为圆心、直径为9 m的圆形区域(见图5)。问题要求我们确定最小螺距,使得龙头前把手能够沿着相应的螺线盘入到调头空间的边界。要求我们计算这个最小螺距的精确值,并分析它对整个板凳龙表演的影响。同时,需要计算使用这个最小螺距时,龙头到达调头空间边界时的确切位置和时间。要求我们按照指定格式将计算结果写入表2,包括最小螺距、龙头到达调头空间边界时的位置坐标和时间。此外,还需要绘制使用最小螺距时的螺线轨迹图,并将其与原始螺距(55 cm)的轨迹进行对比。要求将这个对比图和相关数据保存在附件result3.xlsx中,并在论文中对结果进行详细分析和讨论。
问题四:它指出盘入螺线的螺距为1.7 m,盘出螺线与盘入螺线关于螺线中心呈中心对称。舞龙队在问题3设定的调头空间内完成调头,调头路径是由两段圆弧相切连接而成的S形曲线,前一段圆弧的半径是后一段的2倍,它与盘入、盘出螺线均相切。问题要求我们探讨是否能够调整圆弧,在保持各部分相切的条件下,使调头曲线变短。同时,要求计算整个过程中舞龙队的运动情况。具体要求如下:分析当前调头路径的特性,并探讨可能的优化方案,使调头曲线变短。要求在保持各部分相切的条件下进行优化。龙头前把手的行进速度始终保持1 m/s。以调头开始时间为零时刻,计算从−100 s开始到100 s为止,每秒舞龙队的位置和速度。将计算结果存放到文件result4.xlsx中(模板文件见附件)。在论文中详细给出−100 s、−50 s、0 s、50 s、100 s时,龙头前把手、龙头后面第1、51、101、151、201节龙身前把手和龙尾后把手的位置和速度。绘制舞龙队在整个过程(盘入、调头、盘出)中的运动轨迹图,并在图中标注关键时间点和位置。分析并讨论调头过程对整个表演的影响,包括但不限于表演时间、观赏效果、操作难度等方面。如果找到了更优的调头路径,请比较优化前后的调头时间和路径长度,并讨论这种优化对实际表演可能带来的影响。要求将所有计算结果、图表和分析内容按照指定格式整理到论文中,并将详细数据保存在result4.xlsx文件中。
二、问题分析
本题的研究对象为板凳龙表演,研究的内容为板凳龙运动轨迹的计算方法和表演效果的优化设计。它实际上是一个复杂的动力学和优化问题,要求我们得出板凳龙各节点位置和速度的计算方法,设计板凳龙的相关参数,并达到表演效果最优化的目标。
2.1 问题一分析
对于问题一,分析题目中给出的板凳龙运动方程后,发现它是关于龙头速度 v、螺线参数 a、板凳数量 N、板凳长度 L、初始角度 θ₀ 和时间 t 的函数,且其中大部分参数可从题干中直接得出。因此,求解问题一的关键是板凳龙运动轨迹的确定和各节点位置、速度的计算。首先,等距螺线方程是板凳龙运动轨迹确定的核心。我们由螺线方程 r = a + bθ 得出极坐标下的位置表达式,再通过坐标变换得到直角坐标系下的位置表达式。其次,计算各节点位置和速度的关键在于建立适当的数学模型。我们将板凳龙看作由多个刚性连杆组成的系统,通过建立微分方程组来描述整个系统的运动。对于位置计算,我们利用相邻板凳之间的几何关系,逐个推导出每个节点的位置;对于速度计算,我们利用位置对时间的导数来获得。然后,我们需要设计合适的数值方法来求解这个微分方程组。考虑到问题的非线性特性,我们选择使用龙格-库塔法进行数值求解。这种方法能够在保证精度的同时,有效处理非线性方程。最后,我们将所有参数代入程序中,完成板凳龙各节点位置和速度的求解,并对求解结果进行分析。我们特别关注龙头、特定龙身节点和龙尾在不同时刻的位置和速度,以验证计算结果的正确性和合理性。同时,我们还需要绘制板凳龙在不同时刻的形态图,直观地展示其运动过程。在结果分析中,我们将重点关注板凳龙运动的几个特征:运动的周期性、各节点之间的相对位置关系、速度的变化规律等。这些分析将有助于我们理解板凳龙运动的本质,为后续的优化设计提供重要依据。板凳龙由223节板凳组成,沿螺距为55 cm的等距螺线顺时针盘入,各把手中心均位于螺线上。龙头前把手的行进速度始终保持1 m/s。初始时,龙头位于螺线第16圈A点处。我们需要计算从初始时刻到300 s为止,每秒整个舞龙队的位置和速度。
2.1 问题二分析
对于问题二,我们需要在问题一的基础上进一步分析板凳龙盘入过程的终止条件。关键在于确定板凳之间即将发生碰撞的临界状态,这涉及到板凳之间的最小安全距离的计算和判断。首先,我们需要定义板凳之间的碰撞判定标准。考虑到板凳的实际尺寸和连接方式,我们可以将每个板凳简化为一个线段,并规定当两个相邻板凳之间的最短距离小于某个阈值时,认为发生了碰撞。其次,计算相邻板凳之间最短距离的方法是关键。我们可以利用向量分析,将每个板凳表示为一个向量,然后通过向量运算来计算两个板凳之间的最短距离。这涉及到点到直线距离的计算公式和向量的叉乘、点乘等操作。然后,我们需要设计一个高效的算法来不断推进时间,并在每个时间步长内检查所有相邻板凳对是否满足碰撞条件。考虑到问题的特性,我们可以采用二分法或者逐步逼近的方法来快速定位碰撞发生的临界时刻。接下来,我们需要在程序中实现这个算法,不断计算板凳龙各节点的位置,直到发现第一对相邻板凳满足碰撞条件为止。此时的时刻即为舞龙队盘入的终止时刻。最后,我们将终止时刻代入问题一中的计算方法,得出此时舞龙队各节点的位置和速度。我们需要特别关注龙头前把手、龙头后面第1、51、101、151、201条龙身前把手和龙尾后把手的数据,并将结果保存到result2.xlsx文件中。
-
2.1问题三分析
对于问题三,我们需要确定最小螺距,使得龙头前把手能够沿着螺线盘入到调头空间的边界。这本质上是一个优化问题,涉及到螺线方程的参数调整和边界条件的判断。首先,我们需要明确优化的目标函数。在这个问题中,目标是最小化螺距,同时满足龙头前把手能够到达调头空间边界的约束条件。这要求我们建立螺距与龙头前把手最终位置之间的关系。其次,我们需要建立数学模型来描述龙头前把手的运动轨迹。基于问题一中的螺线方程,我们可以将螺距作为变量,其他参数保持不变。这样,龙头前把手的位置就成为螺距的函数。然后,我们需要定义调头空间边界的数学表达式。根据题目描述,这是一个以螺线中心为圆心、直径为9m的圆形区域。我们可以用圆方程来表示这个边界条件。接下来,我们需要设计一个算法来寻找满足条件的最小螺距。考虑到问题的特性,我们可以采用二分法或者梯度下降法来逐步逼近最优解。在每次迭代中,我们需要:计算当前螺距下龙头前把手的最终位置;判断该位置是否位于调头空间边界上(或非常接近边界);根据判断结果调整螺距的值。最后,我们需要在程序中实现这个优化算法,不断调整螺距的值,直到找到满足条件的最小螺距。
2.4问题四分析
对于问题四,我们需要分析舞龙队的完整运动过程,包括盘入、调头和盘出三个阶段,并探讨调头路径的优化可能性。这个问题涉及到复杂曲线的拼接、运动轨迹的计算以及优化分析。首先,我们需要建立完整的数学模型来描述舞龙队的运动轨迹。这包括:盘入螺线(螺距为1.7m);调头路径(由两段圆弧相切连接而成的S形曲线);盘出螺线(与盘入螺线中心对称)。其次,我们需要精确计算调头路径。这涉及到:确定两段圆弧的半径和圆心位置,计算圆弧与螺线的切点位置,确保两段圆弧之间的相切性。然后,我们需要探讨调头曲线的优化可能性。这需要我们:分析现有调头路径的曲率变化,考虑调整圆弧半径比例的影响,探索其他可能的曲线形式(如贝塞尔曲线)来替代圆弧。我们需要设计算法来计算舞龙队在整个过程中的位置和速度。这包括:在螺线上的运动(使用问题一的方法),在调头路径上的运动(需要新的计算方法),处理不同阶段之间的过渡,最后,我们需要在程序中实现这个算法,计算从-100s到100s每秒舞龙队的位置和速度,并将结果保存到result4.xlsx文件中。
2.5问题五分析
对于问题五,我们需要确定龙头的最大行进速度,使得舞龙队各把手的速度均不超过2 m/s。这是一个优化问题,涉及到复杂的动力学分析和约束条件的处理。首先,我们需要基于问题四的运动模型,建立龙头速度与各节点速度之间的关系。这涉及到:螺线运动阶段的速度传递,调头阶段的速度变化,不同位置节点之间的速度差异,其次,我们需要分析影响各节点速度的因素。这包括龙头速度,节点在板凳龙中的位置,板凳龙所处的运动阶段(盘入、调头、盘出),运动轨迹的曲率,然后,我们需要建立优化模型。目标函数是最大化龙头速度,约束条件是所有节点的速度都不超过2 m/s。这可以表示为:最大化:v_龙头 约束条件:v_i ≤ 2 m/s,对于所有i∈[1, N],其中N是节点总数。接下来,我们需要设计算法来求解这个优化问题。考虑到问题的复杂性,我们可以采用以下方法:从一个较低的龙头速度开始,逐步增加,对每个龙头速度,计算整个运动过程中所有节点的最大速度,当发现任一节点的速度超过2 m/s时,返回上一个有效的龙头速度。最后,我们需要在程序中实现这个算法,找出满足条件的最大龙头速度。
三模型假设
1.理想化板凳:a) 假设每个板凳都是完全刚性的,不会发生形变。b) 所有板凳的质量均匀分布,重心位于几何中心。c) 忽略板凳的厚度,将其视为二维平面上的线段。
2.连接点:a) 假设相邻板凳之间的连接点是理想的铰链,没有摩擦。b) 连接点的尺寸可以忽略不计。
3.运动特性:a) 假设龙头的运动完全遵循给定的螺线方程,不会发生偏离。
b) 忽略重力、空气阻力等外部因素对运动的影响。
c) 假设龙头能够瞬时达到指定速度,加速过程可以忽略。
3.碰撞判定:a) 将板凳间的碰撞简化为线段之间的距离判断。b) 定义一个最小安全距离,当任意两个非相邻板凳之间的最短距离小于此值时,视为发生碰撞。
4.调头过程:a) 假设调头过程中,龙头的速度变化是连续的,没有瞬时的速度跳变。b) 调头路径上的切线速度保持恒定。
5.系统整体:a) 假设整个系统在水平面上运动,忽略垂直方向的运动和影响。b) 板凳龙的总长度在运动过程中保持不变。
6.计算精度:a) 在数值计算中,采用足够小的时间步长,以确保计算精度。
b) 对于连续的曲线(如螺线和调头路径),采用分段线性近似进行离散化处理。
7.观察者视角:a) 假设观察者位于固定的位置,不随板凳龙的运动而移动。
8.环境因素:a) 忽略风力、地面摩擦等环境因素对运动的影响。b) 假设表演场地是理想的平坦地面。
| 符号 | 说明 | 单位 |
| N | 板凳总数 | - |
| L₁ | 龙头板凳长度 | m |
| L₂ | 龙身和龙尾板凳长度 | m |
| W | 板凳宽度 | m |
| d | 孔径 | m |
| h | 孔到板头距离 | m |
| t | 时间 | s |
| x, y | 直角坐标系下的位置 | m |
| r, θ | 极坐标系下的位置 | m, rad |
| a | 螺线初始半径 | m |
| b | 螺距参数 | m/rad |
| p | 螺距 | m |
| v | 速度 | m/s |
| v_h | 龙头速度 | m/s |
| a | 加速度 | m/s² |
| ω | 角速度 | rad/s |
| α | 角加速度 | rad/s² |
| i | 板凳编号索引 | - |
| j | 时间步长索引 | - |
| p_i | 第i个板凳的位置矢量 | m |
| v_i | 第i个板凳的速度矢量 | m/s |
| R | 旋转矩阵 | - |
| C | 螺线中心点 | m |
| D | 调头空间直径 | m |
| d_min | 最小安全距离 | m |
| R₁, R₂ | 调头路径两段圆弧的半径 | m |
| θ₁, θ₂ | 调头路径两段圆弧的圆心角 | rad |
| L_turn | 调头路径总长度 | m |
| r(θ) | 螺线方程 | m |
| x(t), y(t) | 龙头位置随时间的变化函数 | m |
| v(t) | 速度随时间的变化函数 | m/s |
| J | 目标函数 | 取决于优化目标 |
| g(x) | 约束函数 | 取决于约束类型 |
| ε | 容许误差 | 取决于计算对象 |
| δ | 数值计算步长 | 取决于计算对象 |
注:某些符号(如目标函数J和约束函数g(x))的单位可能会根据具体优化问题的定义而变化。
clc;close all;clear;% 常量定义N = 223; % 板凳总数L_HEAD = 3.41; % 龙头长度(m)L_BODY = 2.20; % 龙身和龙尾长度(m)HOLE_DISTANCE = 0.275; % 孔到板头的距离(m)SPIRAL_PITCH = 0.55; % 螺距(m)V_HEAD = 1.0; % 龙头速度(m/s)TOTAL_TIME = 300; % 总时间(s)INITIAL_RADIUS = 16 * SPIRAL_PITCH / (2 * pi); % 初始半径% 定义全局函数global r dr_dtheta theta_dotr = @(theta) INITIAL_RADIUS + SPIRAL_PITCH * theta / (2 * pi);dr_dtheta = @(theta) SPIRAL_PITCH / (2 * pi);theta_dot = @(theta) V_HEAD / sqrt(r(theta)^2 + dr_dtheta(theta)^2);% 求解ODE[t, theta] = ode45(@(t, theta) theta_dot(theta), [0 TOTAL_TIME], 0);% 计算整个舞龙队的位置和速度results = cell(length(t), 1);for i = 1:length(t)positions = zeros(N, 4);for j = 1:Nif j == 1L = L_HEAD;elseL = L_BODY;enddelta_theta = -L / r(theta(i));segment_theta = theta(i) + delta_theta * (j-1);[x, y, vx, vy] = calculate_position_velocity(segment_theta, t(i));positions(j, :) = [x, y, vx, vy];endresults{i} = positions;end% 创建表头headers = {'时间(s)'};for i = 1:Nif i == 1prefix = '龙头(前)';elseif i == Nprefix = '龙尾(后)';elseprefix = sprintf('龙身%d', i-1);endheaders = [headers, ...sprintf('%s_x', prefix), ...sprintf('%s_y', prefix), ...sprintf('%s_vx', prefix), ...sprintf('%s_vy', prefix)];end% 准备数据data = cell(length(t), 1 + N * 4);for i = 1:length(t)row = [t(i), reshape(results{i}', 1, [])];data(i, :) = num2cell(row);end% 创建表格并保存到ExcelT = cell2table(data, 'VariableNames', headers);writetable(T, 'result1.xlsx');% 打印特定时间点的结果print_times = [0, 60, 120, 180, 240, 300];print_segments = [1, 2, 52, 102, 152, 202, N];for t_idx = 1:length(print_times)t_val = print_times(t_idx);[~, idx] = min(abs(t - t_val));fprintf('\n时间: %ds\n', t_val);fprintf('节点\t\tx\t\ty\t\tvx\t\tvy\n');for seg = print_segmentsx = results{idx}(seg, 1);y = results{idx}(seg, 2);vx = results{idx}(seg, 3);vy = results{idx}(seg, 4);if seg == 1name = '龙头(前)';elseif seg == Nname = '龙尾(后)';elsename = sprintf('龙身%d', seg-1);endfprintf('%s\t%.6f\t%.6f\t%.6f\t%.6f\n', name, x, y, vx, vy);endend% 绘制最终位置final_positions = results{end};figure;plot(final_positions(:, 1), final_positions(:, 2), 'b-', 'LineWidth', 2);hold on;plot(final_positions(1, 1), final_positions(1, 2), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r'); % 龙头plot(final_positions(end, 1), final_positions(end, 2), 'go', 'MarkerSize', 10, 'MarkerFaceColor', 'g'); % 龙尾title('板凳龙最终位置 (300s)');xlabel('X (m)');ylabel('Y (m)');legend('龙身', '龙头', '龙尾');axis equal;grid on;% 计算位置和速度function [x, y, vx, vy] = calculate_position_velocity(theta, ~)global r dr_dtheta theta_dotradius = r(theta);x = radius * cos(theta);y = radius * sin(theta);v_r = dr_dtheta(theta) * theta_dot(theta);v_theta = r(theta) * theta_dot(theta);vx = v_r * cos(theta) - v_theta * sin(theta);vy = v_r * sin(theta) + v_theta * cos(theta);end