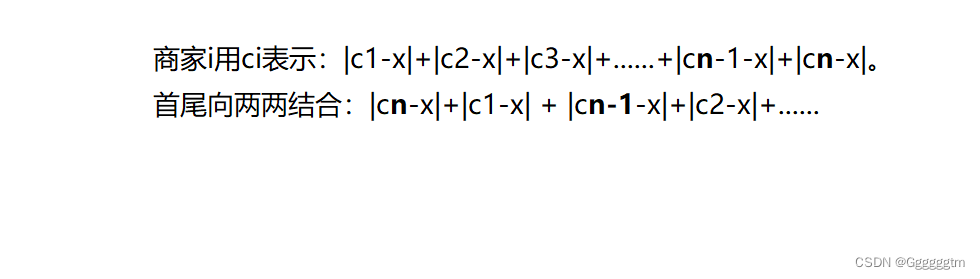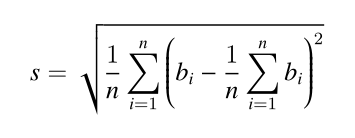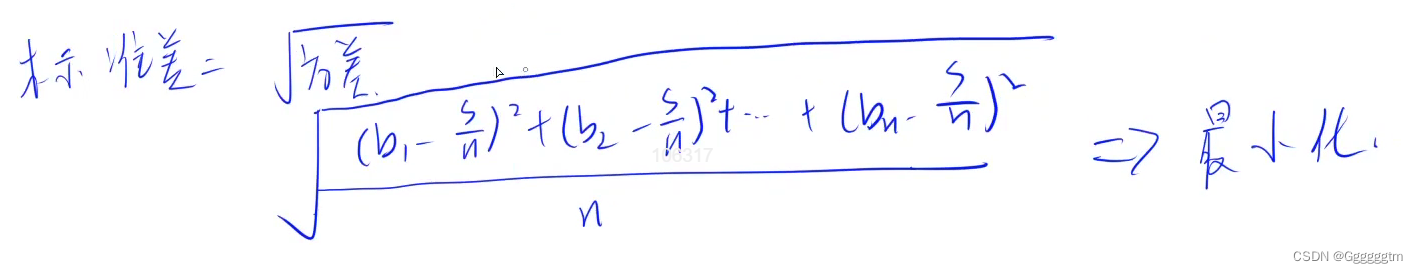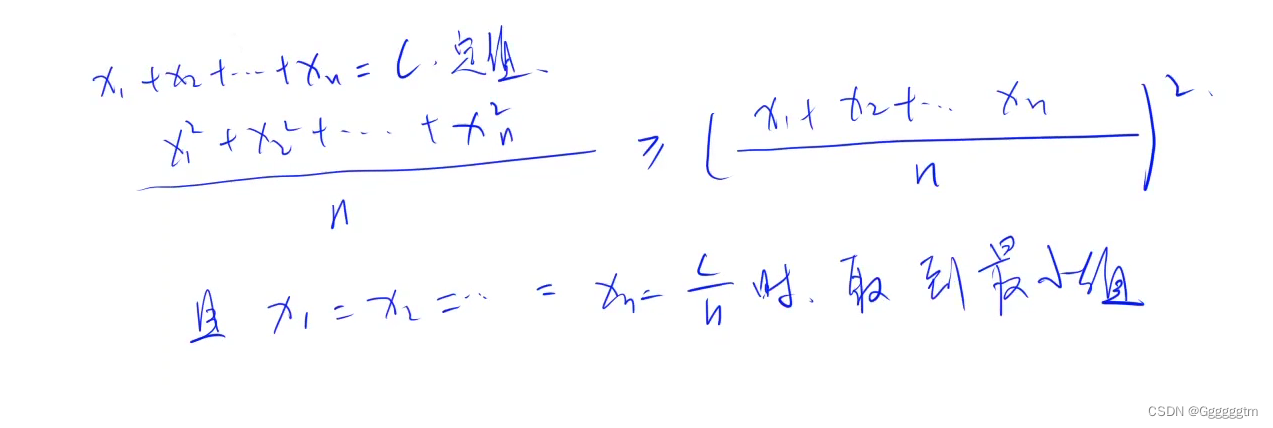[蓝桥杯] 贪心问题与相关习题详解

目录
一、什么是贪心算法呢?
二、股票买卖 II
2、1 题目描述
2、2 题解关键思路与解答
三、货仓选址
3、1 题目描述
3、2 题解关键思路与解答
四、雷达设备
4、1 题目描述
4、2 题解关键思路与解答
五、付账问题
5、1 题目描述
5、2 题解关键思路与解答
六、总结
🙋♂️ 作者:@Ggggggtm 🙋♂️
👀 专栏:数据结构与算法 👀
💥 标题:贪心算法——蓝桥杯 💥
❣️ 寄语:与其忙着诉苦,不如低头赶路,奋路前行,终将遇到一番好风景 ❣️
本片文章同样是针对蓝桥杯的考点,列出关于贪心算法的相关习题,并且对其进行了讲解。同时也会给出贪心算法的解释。
一、什么是贪心算法呢?
什么是贪心算法呢?
贪心算法是一种基于贪心策略的算法,它在每一步都选择当前最优解,从而得到全局最优解。贪心算法通常用于优化问题,如最小生成树、最短路径、背包问题等。其基本思想是:在每一步中,选择当前最优解,并将其加入到已知的解集合中。然后,将问题缩小到剩余的未解决部分,并重复上述步骤,直到得到全局最优解。
例如,对于背包问题,贪心算法可以按照物品的单位价值从大到小排序,然后依次将单位价值最高的物品放入背包中,直到背包无法再放入物品为止。这样可以得到一个近似最优解。
需要注意的是,贪心算法并不一定能够得到全局最优解,因为它只考虑了当前最优解,而没有考虑到未来的影响。因此,在使用贪心算法时,需要仔细分析问题,确保贪心策略的正确性。贪心的模型有很多,贪心的结果也很难想到,这就导致了很多贪心的题目相对比较难。下面我们结合着几个例题一起理解一下贪心。
二、股票买卖 II
2、1 题目描述
题目来源:《算法竞赛进阶指南》, LeetCode
题目难度:简单
题目描述: 给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
输入格式:
第一行包含整数 N,表示数组长度。
第二行包含 N 个不大于 10000 的正整数,表示完整的数组。
输出格式:
输出一个整数,表示最大利润。
数据范围:
1≤N≤105
输入样例1:
6 7 1 5 3 6 4输出样例1:
7输入样例2:
5 1 2 3 4 5输出样例2:
4输入样例3:
5 7 6 4 3 1输出样例3:
0样例解释:
样例1:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。共得利润 4+3 = 7。
样例2:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
样例3:在这种情况下, 不进行任何交易, 所以最大利润为 0。
2、2 题解关键思路与解答
这道题目中最优解的方案可能不止一个。我们看样例1,是后一天比前一天股票价格大的时候我们把股票买入,同时在后一天卖出。这样就能获得利润。我们再看样例2,是在第一天买入,第五天卖出。我们可以把它拆解成四小段,也就是前一天买入,后一天卖出。结果是一样的。因此,我们可以想到任何一大段时间的股票买卖都可以拆解成很多段两天的股票买卖。当转换为两天的股票买卖时,我们只需要考虑是否盈利就行(如样例1的分析)。只要找到没两天的盈利相加就是最大盈利值。我们看代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int n;
int price[N];
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&price[i]);
}
int res=0;
for(int i=0;i<n-1;i++)
{
if(price[i]<price[i+1])
res+=price[i+1]-price[i];
}
printf("%d",res);
return 0;
}三、货仓选址
3、1 题目描述
题目来源:《算法竞赛进阶指南》, Acwing模板题
题目难度:简单
题目描述:在一条数轴上有 N 家商店,它们的坐标分别为 A1∼AN。现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送一车商品。为了提高效率,求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。
输入格式:
第一行输入整数 N。
第二行 N 个整数 A1∼AN。
输出格式:
输出一个整数,表示距离之和的最小值。
数据范围:
1≤N≤100000,
0≤Ai≤40000。输入样例:
4 6 2 9 1输出样例:
12
3、2 题解关键思路与解答
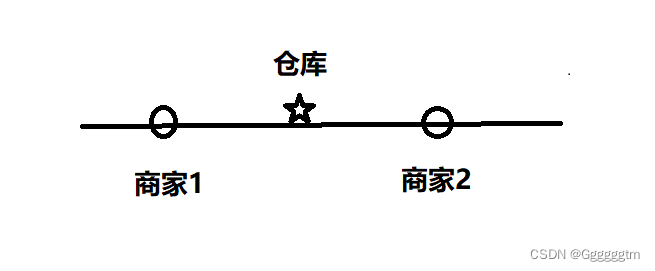
相信很多人在读到着道题目的时候都会感觉很熟悉。模糊的记忆中好像是在初中的时候做过类似的数学题。那应该怎么选呢?我们先看只有两个商家的情况:
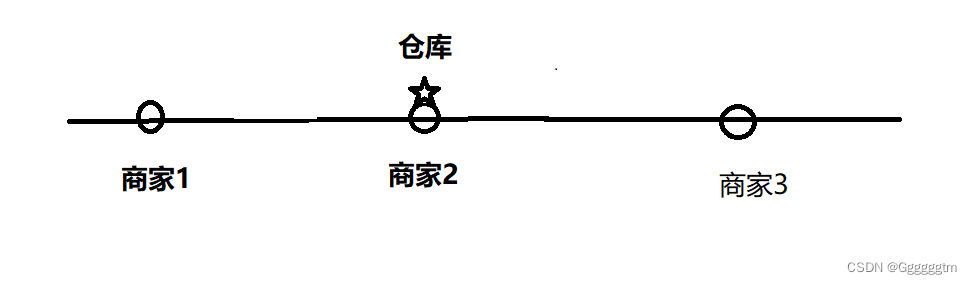
这个时候我们发先,仓库选到商家1和商家2之间为货仓到每家商店的距离之和最小,即为两个商家之间的距离。我们再来看三个商家的情况:
当有三个商家的时候,我们把货舱宣导中间位置的商家(如图中的商家2)可使得货仓到每家商店的距离之和最小。我们大概猜出的多个商家时货舱的选址了,当商家个数为奇数时,我们选货舱的地址为商家位置的中位数,商家个数为偶数时,我们选货舱的地址为中间位置两个商家之间的任何一个点即可。为什么呢?
假设有n个商家:
我们把货舱的位置宣导了x的位置,那么我们得出公式:
两两结合阶变成了求都组两个点之间的距离的最小值。当商家个数为奇数时,我们选货舱的地址为商家位置的中位数,商家个数为偶数时,我们选货舱的地址为中间位置两个商家之间的任何一个点。我们来看代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e5+10;
int a[N];
int n;
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&a[i]);
sort(a,a+n);
int mid=n/2;
LL cnt=0;
for(int i=0;i<n;i++)
{
cnt+=abs(a[i]-a[mid]);
}
cout<<cnt;
return 0;
}四、雷达设备
4、1 题目描述
题目来源:《算法竞赛进阶指南》
题目难度:中等
题目描述:假设海岸是一条无限长的直线,陆地位于海岸的一侧,海洋位于另外一侧。
每个小岛都位于海洋一侧的某个点上。雷达装置均位于海岸线上,且雷达的监测范围为 d,当小岛与某雷达的距离不超过 d 时,该小岛可以被雷达覆盖。我们使用笛卡尔坐标系,定义海岸线为 x 轴,海的一侧在 x 轴上方,陆地一侧在 x 轴下方。现在给出每个小岛的具体坐标以及雷达的检测范围,请你求出能够使所有小岛都被雷达覆盖所需的最小雷达数目。
输入格式:
第一行输入两个整数 n 和 d,分别代表小岛数目和雷达检测范围。
接下来 n 行,每行输入两个整数,分别代表小岛的 x,y 轴坐标。
同一行数据之间用空格隔开。
输出格式:
输出一个整数,代表所需的最小雷达数目,若没有解决方案则所需数目输出 −1−1。
数据范围:
1≤n≤1000,
−1000≤x,y≤1000。输入样例:
3 2 1 2 -3 1 2 1输出样例:
2
4、2 题解关键思路与解答
通过分析题目我们知道,雷达只能在海岸线上,也就是只能在x轴上。我们需要做的是根据某一个小岛,找出在海岸线的一段区间,在这段区间中安装雷达都可探测到该小岛。我们需要记录下该所有这样的区间,然后根据区间的右端点进行排序。只要区间有重叠的部分,雷达的位置我们就选第一个区间的右端点即可。如果不重叠,新增加一个雷达,为新的不重叠区间的右端点。这样算出来的雷达的数量最少。特殊情况需要独判一下。我们结合代码一起理解一下:
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
struct query
{
double l,r;
bool operator< (const query &t) const
{
return r<t.r;
}
}q[N];
int main()
{
int n,d;
scanf("%d%d",&n,&d);
bool failed = false;
for(int i=0;i<n;i++)
{
int x,y;
scanf("%d%d",&x,&y);
if(y>d)
failed=true;
else
{
double len=sqrt(d*d-y*y);
q[i]={x-len,x+len};
}
}
int cnt=0;
if(failed)
puts("-1");
else
{
sort(q,q+n);
double last=-1e20;
for(int i=0;i<n;i++)
{
if(last<q[i].l)
{
cnt++;
last=q[i].r;
}
}
cout<<cnt;
}
return 0;
}五、付账问题
5、1 题目描述
题目来源:第九届蓝桥杯省赛C++A组,第九届蓝桥杯省赛JAVAA组
题目难度:中等
题目描述:几个人一起出去吃饭是常有的事。但在结帐的时候,常常会出现一些争执。现在有 n 个人出去吃饭,他们总共消费了 S 元。其中第 i 个人带了 ai 元。幸运的是,所有人带的钱的总数是足够付账的,但现在问题来了:每个人分别要出多少钱呢?为了公平起见,我们希望在总付钱量恰好为 S 的前提下,最后每个人付的钱的标准差最小。这里我们约定,每个人支付的钱数可以是任意非负实数,即可以不是 11 分钱的整数倍。你需要输出最小的标准差是多少。
标准差的介绍:标准差是多个数与它们平均数差值的平方平均数,一般用于刻画这些数之间的“偏差有多大”。形式化地说,设第 i 个人付的钱为 bi 元,那么标准差为 :
输入格式:
第一行包含两个整数 n、S;
第二行包含 n 个非负整数 a1, …, an。
输出格式:
输出最小的标准差,四舍五入保留 4 位小数。
数据范围:
1≤n≤5×1e5
0≤ai≤1e9,
0≤S≤1e15。输入样例1:
5 2333 666 666 666 666 666输出样例1:
0.0000输入样例2:
10 30 2 1 4 7 4 8 3 6 4 7输出样例2:
0.7928
5、2 题解关键思路与解答
该题的问题是:
那我们应该先了解一下如下公式:
我们知道在本题中x1+x2+x3+……+xn的值为0,也就是当x1、x2、x3……xn取到0为最小值。那么我们在求bi的时候就应该接近均值,我们才能求到方差的最小值。我们结合代码理解一下:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=5e5+10;
int n;
long double s;
int a[N];
int main()
{
cin>>n>>s;
long double cur=0,avg=s/n,res=0;
for(int i=0;i<n;i++)
{
scanf("%d",&a[i]);
}
sort(a,a+n);
for(int i=0;i<n;i++)
{
cur=s/(n-i);
if(a[i]<cur)
cur=a[i];
res+=(cur-avg)*(cur-avg);
s-=cur;
}
printf("%.4Lf",sqrt(res/n));
return 0;
}六、总结
以上就是关于贪心的讲解和例题。其中都是针对蓝桥杯的考点例出的题型。贪心的模型较多,我们需要多刷题进行总结,从而达到熟练的程度。希望以上内容对你有所帮助。感谢阅读ovo~