FloodFill算法【下】

417. 太平洋大西洋水流问题

题目链接：417. 太平洋大西洋水流问题

题目解析

题目给我们一个矩阵，这个矩阵相当于陆地，被两个洋包围，左和上代表太平洋，右和下代表大西洋。

矩阵里面的数字代表海拔，水可以从较高处流向较低处或者流向和自己海拔一样的。

题目要求出既能流向太平洋，又能流向大西洋的区域，返回坐标。

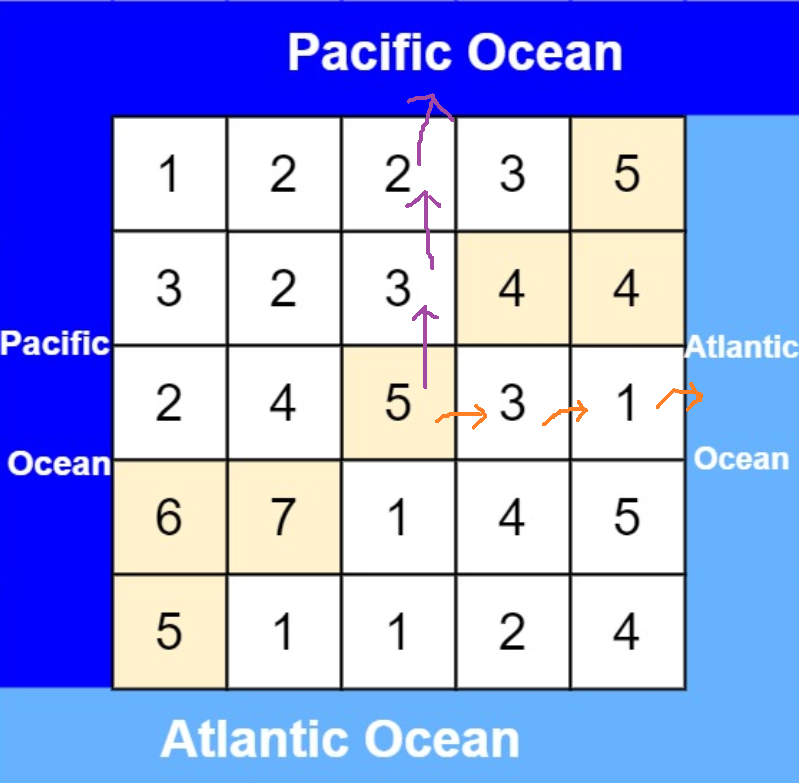
算法原理

解法一：直接判定

遍历一个点就看是否能流入太平洋和大西洋，能的话就保存该位置。

这个方法会有很多重复的逻辑，比如说：

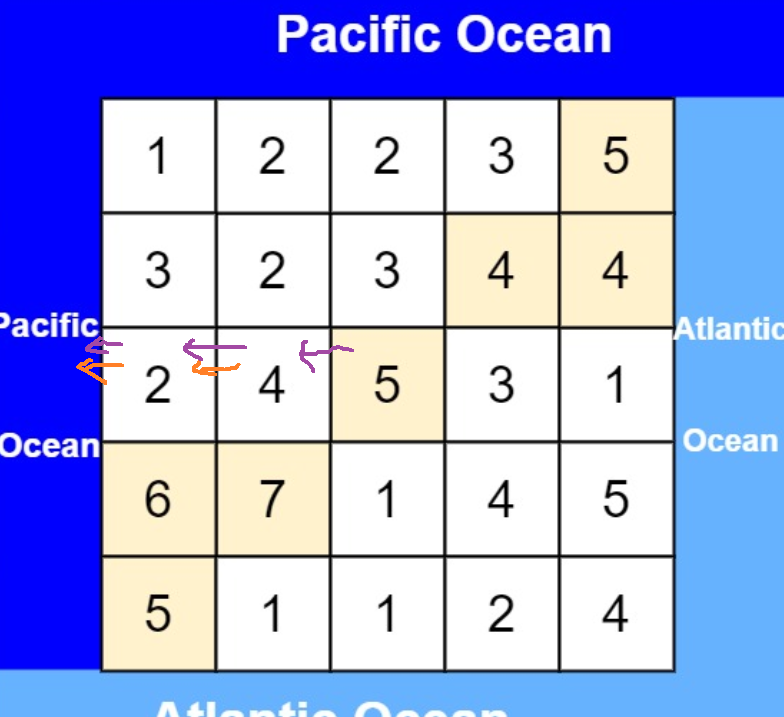
解法二：正难则反

我们可以考虑洋可以反着流进哪些位置，找出交集即可

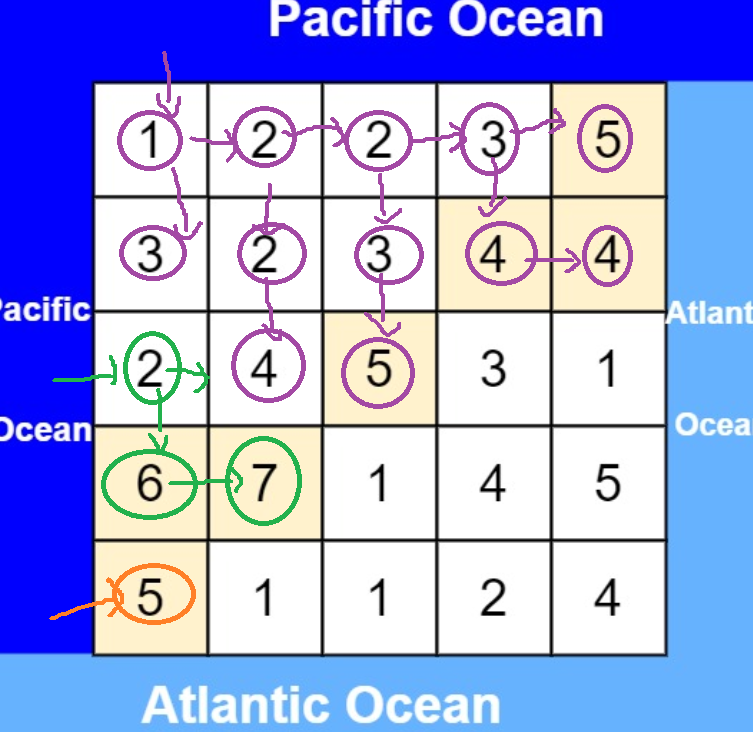
代码实现

class Solution {
public:
    int m = 0;
    int n = 0;
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {-1, 1, 0, 0};
    vector<vector<int>> ret;

    vector<vector<int>> pacificAtlantic(vector<vector<int>>& h)
    {
        m = h.size();
        n = h[0].size();

        vector<vector<bool>> pac(m, vector<bool> (n));
        vector<vector<bool>> atl(m, vector<bool> (n));

        //pac 从第一行和第一列流入
        for(int j = 0; j < n; j++)  dfs(h, 0, j, pac);
        for(int i = 0; i < m; i++)  dfs(h, i, 0, pac);

        //atl 从最后一行和最后一列流入
        for(int j = 0; j < n; j++)  dfs(h, m-1, j, atl);
        for(int i = 0; i < m; i++)  dfs(h, i, n-1, atl);

        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(pac[i][j] && atl[i][j])
                    ret.push_back({i, j});
            }
        }
        return ret;
    }

    void dfs(vector<vector<int>>& h, int i, int j, vector<vector<bool>>& vis)
    {
        vis[i][j] = true;
        for(int k = 0; k < 4; k++)
        {
            int x = dx[k] + i;
            int y = dy[k] + j;
            if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && h[x][y] >= h[i][j])
                dfs(h, x, y, vis);
        }
    }
};

529. 扫雷游戏

题目链接：529. 扫雷游戏

题目解析

扫雷游戏规则就不多说了…

题目让我们返回点击一次之后，棋盘的结果

算法原理

读懂题目就是算法原理了，主要是把思路通过代码模拟出来

代码实现

class Solution {
public:
    int m = 0;
    int n = 0;
    int dx[8] = {0, 0, 1, -1, 1, 1, -1, -1};
    int dy[8] = {1, -1, 0, 0, 1, -1, 1, -1};
    vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click)
    {
        m = board.size();
        n = board[0].size();
        int x = click[0];
        int y = click[1];
        if(board[x][y] == 'M')
        {
            board[x][y] = 'X';
            return board;
        }
        dfs(board, x, y);
        return board;
    }

    void dfs(vector<vector<char>>& board, int i, int j)
    {
        int mCount = 0;
        for(int k = 0; k < 8; k++)
        {
            int x = dx[k] + i;
            int y = dy[k] + j;
            if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'M')
            {
                mCount++;
            }    
        }

        if(mCount)
        {
            board[i][j] = mCount + '0';
            return;
        }
        else
        {
            board[i][j] = 'B';
            for(int k = 0; k < 8; k++)
            {
                int x = dx[k] + i;
                int y = dy[k] + j;
                if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'E')
                {
                    dfs(board, x, y);
                }    
            }
        }


    }
};

LCR 130. 衣橱整理

题目链接：LCR 130. 衣橱整理

题目解析

直接看图示例：

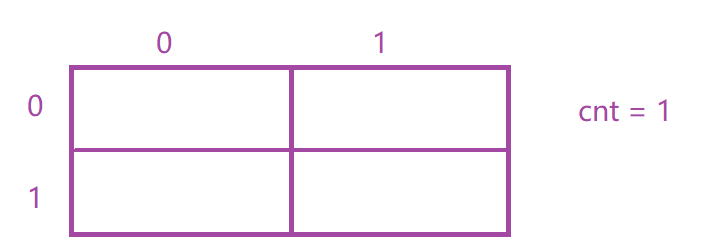
每次向下或者向右移动，grid[i][j]，假设i == 21， j == 31，将它们每位分解，然后做加法(2+1) + (3+1)，看是是否<=cnt即可

算法原理

从(0, 0)位置进行一次深度优先遍历，统计满足要求的格子个数即可

• 分解数位之和
• 标记扫描过的地方

代码实现

class Solution {
public:
    int digit(int num)
    {
        int ret = 0;
        while(num)
        {
            ret += num%10;
            num /= 10;
        }
        return ret;
    }

    int cnt = 0;
    int m = 0;
    int n = 0;
    int ret = 0;
    int dx[2] = {0, 1};
    int dy[2] = {1, 0};
    bool check[100][100];
    int wardrobeFinishing(int _m, int _n, int _cnt)
    {
        cnt = _cnt;
        m = _m;
        n = _n;

        dfs(0, 0);
        return ret;
    }

    void dfs(int i, int j)
    {
        check[i][j] = true;
        ret++;
        for(int k = 0; k < 2; k++)
        {
            int x = dx[k] + i;
            int y = dy[k] + j;
            if(x < m && y < n && !check[x][y] && (digit(x)+digit(y)) <= cnt)
            {
                dfs(x, y);
            }
        }
    }
};