数据结构——树(终极版)
树的基本概念:
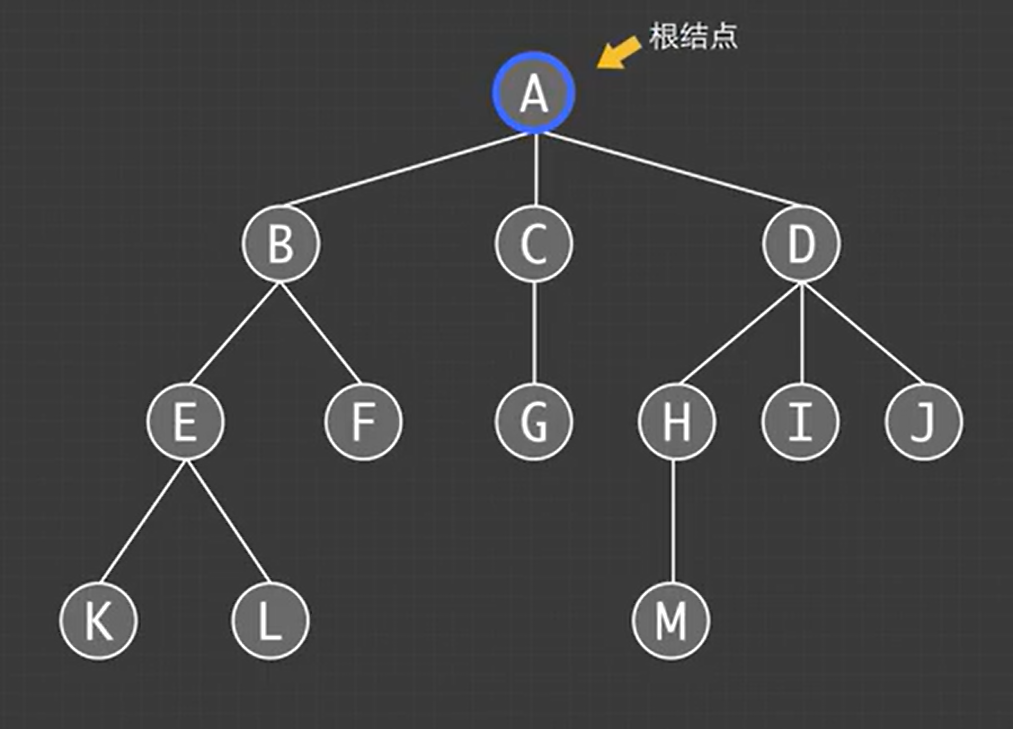
树的顶部是根节点也是树的入口
父节点:例如:B是F的父节点
子节点:树中的每个节点都可以有0个或多个子节点
叶子节点:像KLFGMIJ这种没有子节点的节点
节点的度:节点的子节点数;例如:B的度为2,D的度为3
树的度:所有节点最大度称为该树的度,该树的度为3
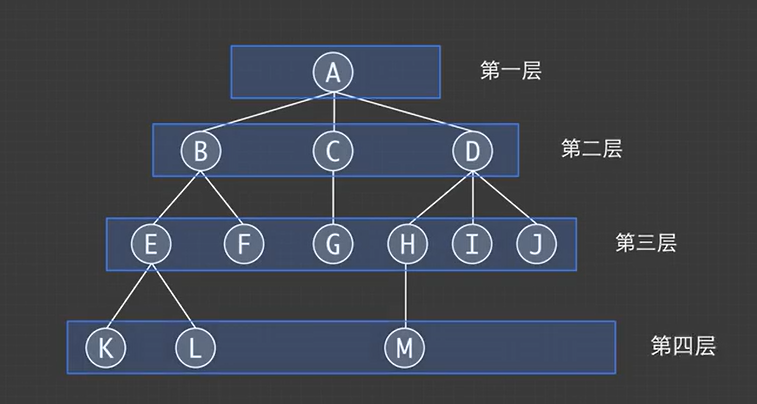
节点的层次:可以表示该节点在树中的相对位置
堂兄弟节点:双亲在同一层;例如:G和H的双亲在同一层,则G和H为堂兄弟节点
节点深度:从根节点开始,达到指定节点的层数为节点深度,例如,D的层数为2所以深度为2
节点高度:从该结点出发到离它最远的叶子节点的层数,例如D出发到M的距离为2,所以D的高度为2
树的高度/深度:指的是该树最大的层数,该树最大的层数为4
二叉树:
单节点树:有一个结点的树
空结点树:根节点为空、
左斜树:只有左子节点
右斜树:只有右子节点


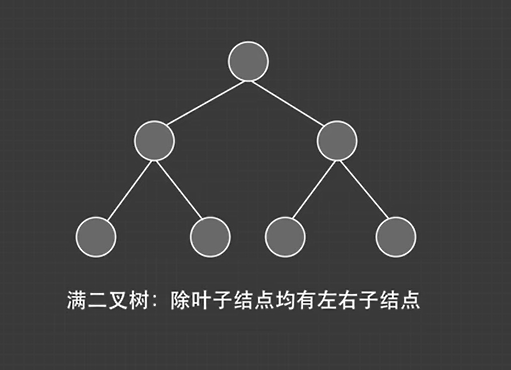
满二叉树:
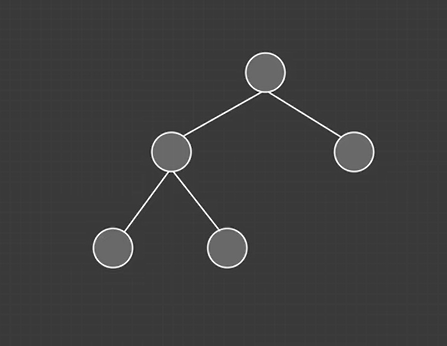
完全二叉树:
除叶子节点以外所有节点必须填满,并且叶子节点要靠左排序
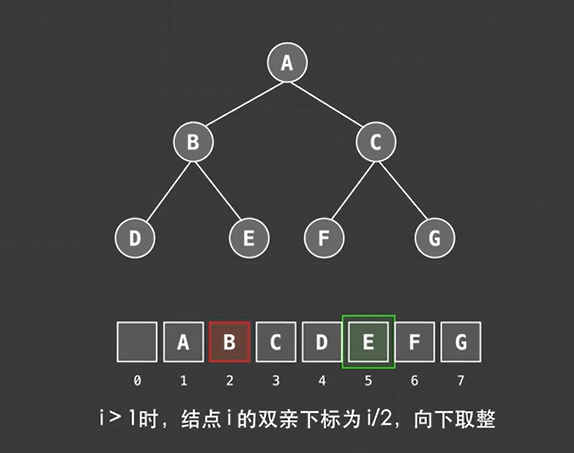
数组存储二叉树:
数组存储方式主要适用于满二叉树或完全二叉树,
用数组存储中要求节点的位置与索引之间存在明确的映射关系,这种映射关系是按照完全二叉树或满二叉树设计的,如果不是完全二叉树则会浪费一些空间用空位来表示空缺节点
使用数组存储利用率较低,一般使用链表存储
左子:
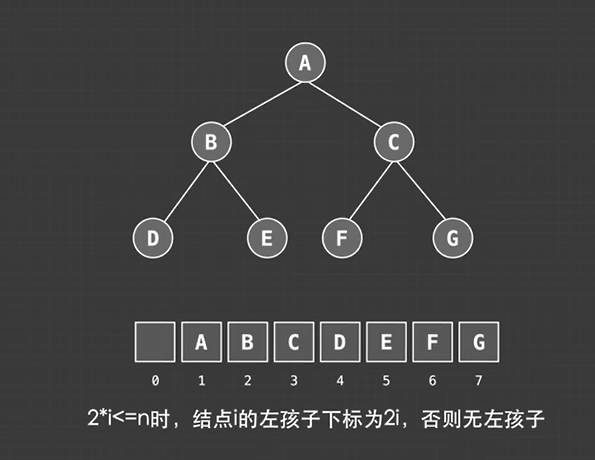
右子:
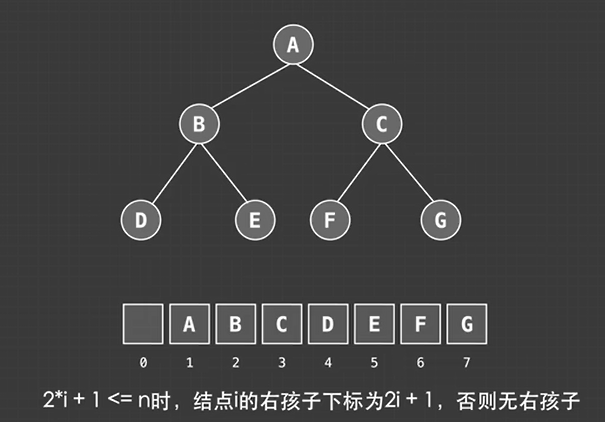
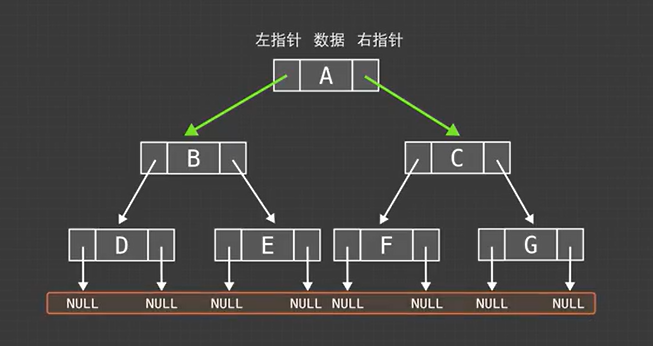
二叉树的链表存储:
二叉树结点数:n
指针域数量:2n
非空指针域数:n-1(减去的为根节点)
空指针域数量:n+1
0.递归:
递:将问题拆解成子问题,子问题再拆解为子问题,直到被拆解的问题是最小的子问题
归:最小的子问题被解决了那么上一层也被解决,上上一次也被解决,一直到最开始的问题被解决
编程中,在函数调用本身

1.树的存储结构:
双亲表示法:
用的数组存储
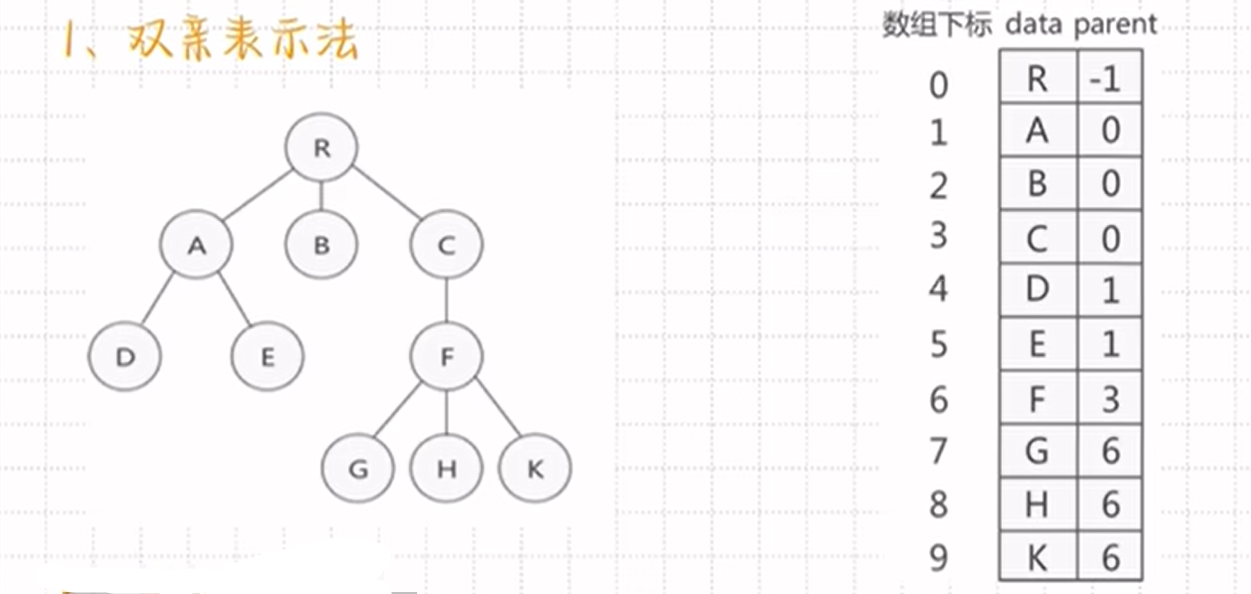
孩子表示法:
用链表
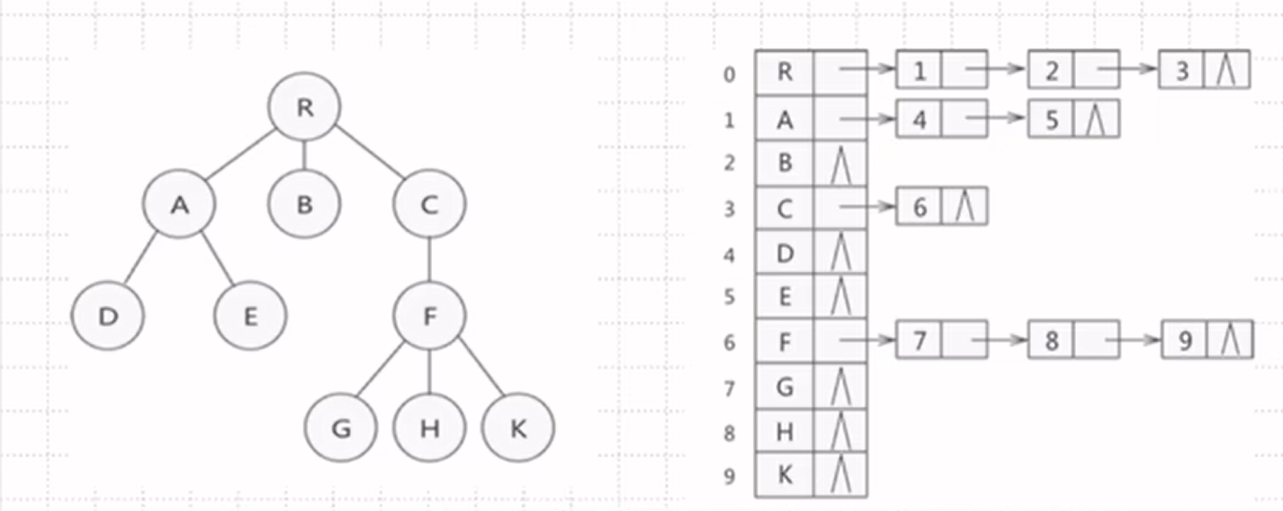
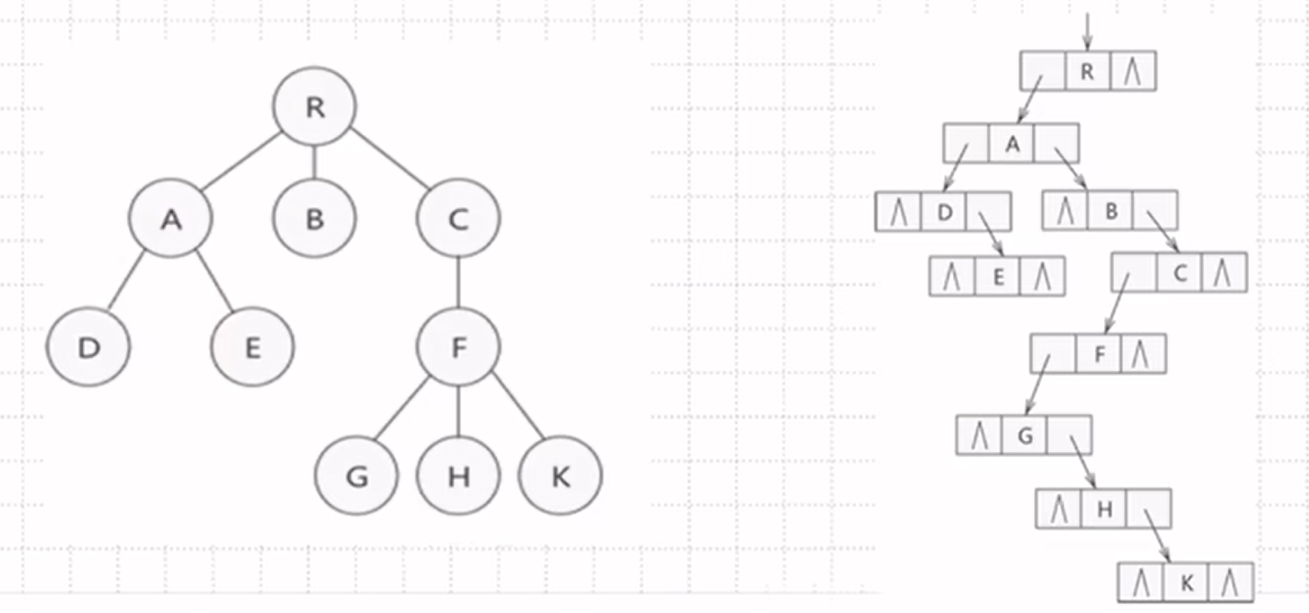
孩子兄弟表示法:
用二叉链表存储
也就是说链表左指针指向第一个孩子,右指针指向兄弟
例如:A的左指针指向左孩子D,右指针指向兄弟B,B没有孩子左指针制空,右指针指向兄弟C
2.二叉树的遍历:
前序遍历:
遍历顺序:根、左、右

void PreOrder(BiTree T){
if(T != NULL){
visit(T); //访问根节点
PreOrder(T->lchild); //递归遍历左子树
PreOrder(T->rchild); //递归遍历右子树
}
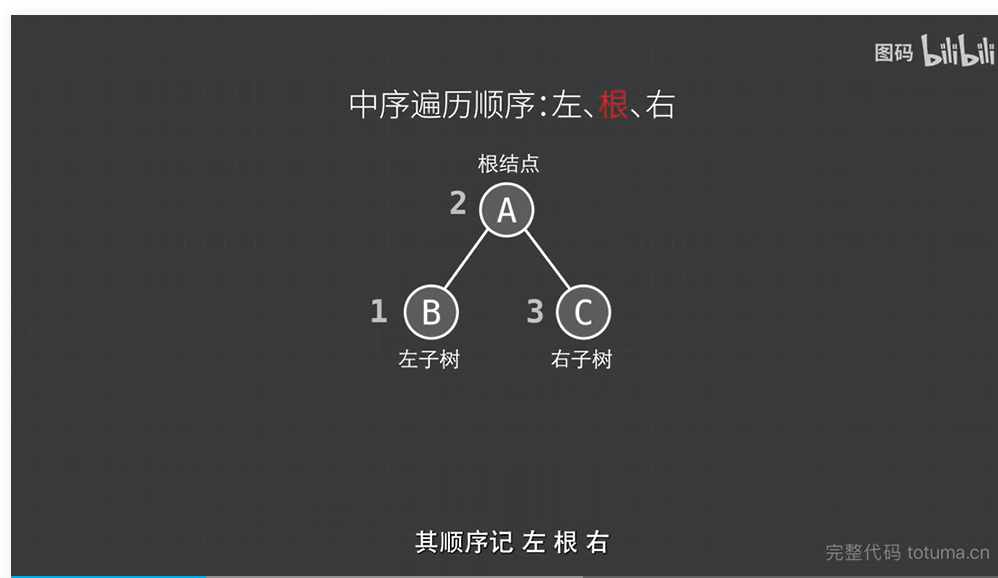
}中序遍历:
遍历顺序:左根右
void InOrder(BiTree T){
if(T != NULL){
InOrder(T->lchild); //递归遍历左子树
visit(T); //访问根结点
InOrder(T->rchild); //递归遍历右子树
}
}后序遍历:
遍历顺序:左右根

void InOrder(BiTree T){
if(T != NULL){
InOrder(T->lchild); //递归遍历左子树
visit(T); //访问根结点
InOrder(T->rchild); //递归遍历右子树
}
}例题:
前序遍历:A B D E C F G
中序遍历:D B E A F C G
后序遍历: D E B F G C A

层次遍历:
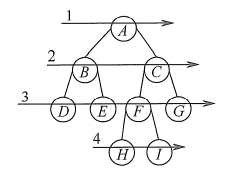
按照层次遍历:A B C D E F G H I
3.线索二叉树:
线索二叉树是一种改进的二叉树,其中空指针(即没有左右子树的节点)被用来指向节点的前驱或后继。这样可以在遍历树时更高效地访问节点,而不需要使用额外的栈或递归。
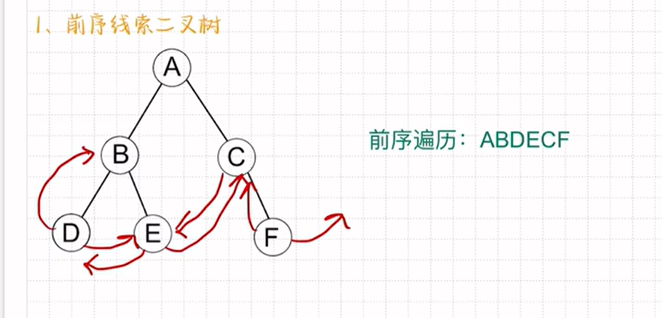
前序线索二叉树:
先把二叉树进行前序遍历
像D E C F这种有空指针的将它们的指针指向前驱。
例如:D前驱节点指向B后驱节点指向E,F前驱节点指向C后驱节点为NULL
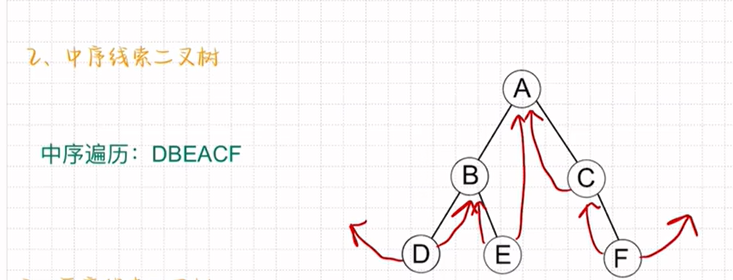
中序线索二叉树:
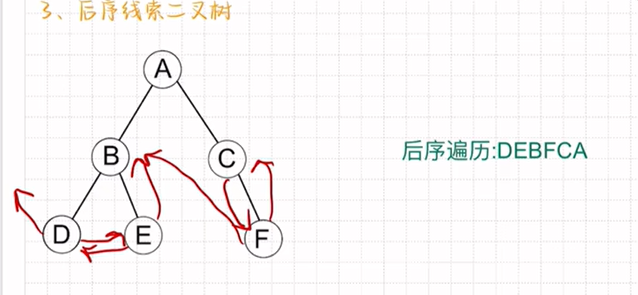
后序线索二叉树:
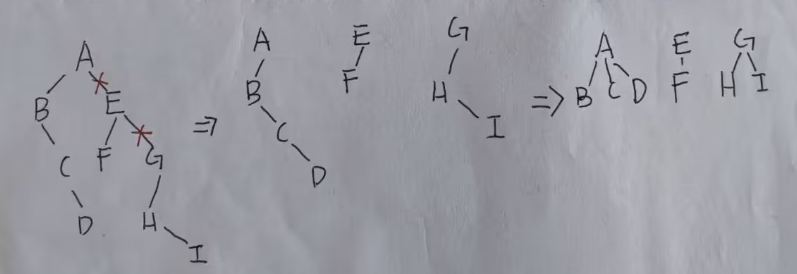
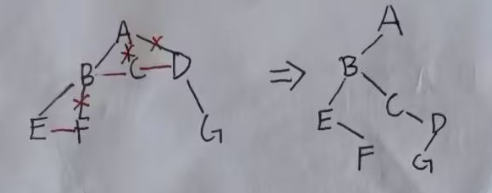
4.森林、树、二叉树之间的转换
树转换为二叉树:
- 每层连线
- 把多余的枝子减去
- 调整形状
我感觉有点像那个孩子兄弟表示法,孩子放左边,孩子的兄弟放右边
二叉树转为树:
- 右分支水平拉起
- 连接每层老大的双亲
- 删掉水平线
就是把右边的兄弟都放到该放的位置上
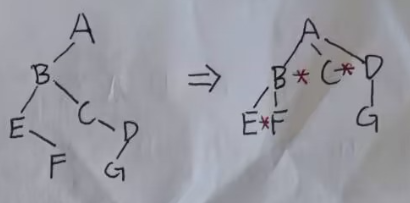
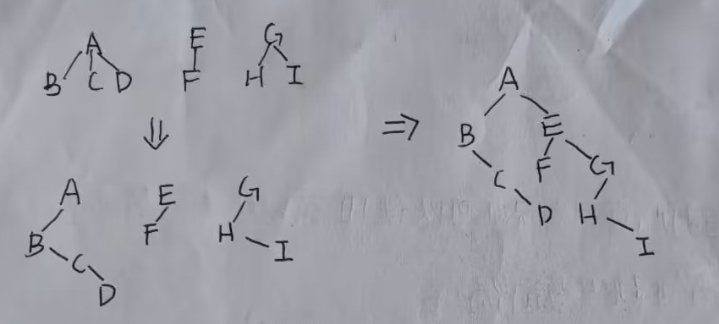
森林转二叉树
- 森林先分别转为二叉树
- 前者的根右分支连接后者的根节点
二叉树转为森林:
- 如果二叉树根节点右右孩子,切断联系
- 然后把每棵二叉树转为树