【电力系统】基于遗传算法的33节点电力系统无功优化及MATLAB实现

摘要
本文研究了基于遗传算法的33节点配电系统的无功优化问题。通过调整电容器的安装位置和容量,以最小化系统的无功损耗和电压偏差。研究使用遗传算法对无功优化问题进行求解,并在MATLAB环境中进行仿真实现。实验结果表明,该方法能够有效地提高系统的电压稳定性和减少无功损耗。
理论
无功优化是配电网中常见的问题,其主要目标是通过优化电容器的配置,减少系统中的无功损耗和改善电压分布。遗传算法作为一种全局优化算法,通过模拟生物进化过程中的选择、交叉和变异等机制来寻找问题的最优解。本文采用以下步骤进行无功优化:
-
初始化种群:随机生成电容器的位置和容量作为初始种群。
-
适应度函数:适应度函数定义为无功损耗和电压偏差的加权和。目标是最小化适应度值。
-
选择操作:使用轮盘赌或锦标赛选择方法,从种群中选取适应度值较好的个体。
-
交叉操作:通过交叉操作生成新的个体,从而在解空间中探索新的解。
-
变异操作:在交叉后对个体进行随机变异,以增加种群的多样性。
-
迭代优化:不断迭代选择、交叉和变异操作,直到达到预定的迭代次数或适应度值收敛。
实验结果
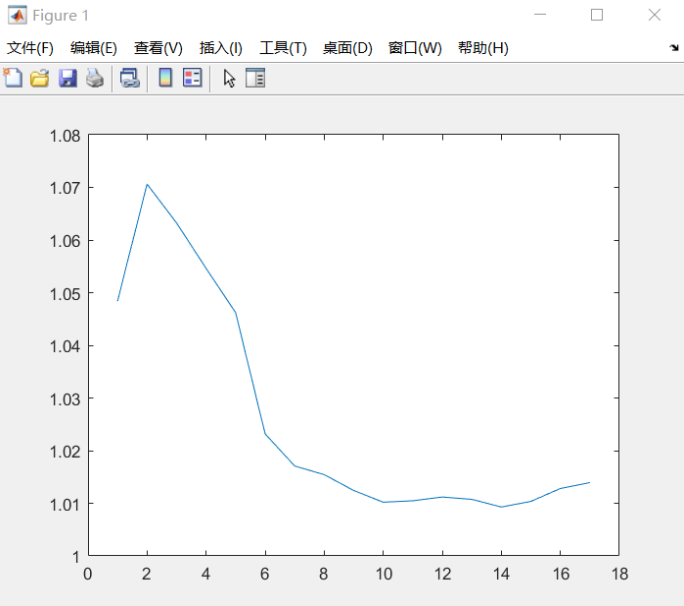
使用MATLAB对33节点系统进行仿真,通过调整遗传算法的参数(如种群规模、交叉概率和变异概率)来优化算法性能。实验结果表明,与传统方法相比,遗传算法能够更有效地减少无功损耗并提高电压稳定性。下图展示了适应度函数随迭代次数的变化情况,可以看出,适应度值逐渐下降并收敛到较小的值,表明系统性能得到了有效提升。
部分代码
% 初始化遗传算法参数
population_size = 50; % 种群规模
crossover_rate = 0.8; % 交叉概率
mutation_rate = 0.01; % 变异概率
max_generations = 100; % 最大迭代次数
% 初始化种群
population = initialize_population(population_size);
% 迭代优化过程
for generation = 1:max_generations
% 评估种群适应度
fitness = evaluate_fitness(population);
% 选择操作
selected_population = selection(population, fitness);
% 交叉操作
offspring_population = crossover(selected_population, crossover_rate);
% 变异操作
mutated_population = mutation(offspring_population, mutation_rate);
% 更新种群
population = mutated_population;
% 记录当前最优适应度值
best_fitness(generation) = min(fitness);
end
% 显示结果
plot(1:max_generations, best_fitness);
xlabel('Generation');
ylabel('Best Fitness');
title('Convergence Curve');
参考文献
❝
Glover, F., & Kochenberger, G. A. (2003). Handbook of metaheuristics. Springer Science & Business Media.
Goldberg, D. E. (1989). Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley Publishing Company.
Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. In Proceedings of ICNN'95-International Conference on Neur

