数据处理与统计分析篇-day10-Matplotlib数据可视化

数据可视化简介

可视化介绍

1. 数据可视化是指直观展现数据，它是数据处理过程的一部分。

2. 把数值绘制出来更方便比较。借助数据可视化，能更直观地理解数据，这是直接查看数据表做不到的

3. 数据可视化有助于揭示数据中隐藏的模式，数据分析时可以利用这些模式选择模型

可视化库介绍

基于Matplotlib 绘制静态图形

1. pandas

2. seaborn

基于JS (javaScript)

1. pyecharts/echarts

2. plotly

Matplotlib的API介绍

Matplotlib提供了两种方法作图: 状态接口 和 面向对象

import numpy as np
​
import matplotlib.pyplot as plt
​
plt.rcParams['font.sans-serif'] = ['SimHei']  # 正常显示汉字
plt.rcParams['axes.unicode_minus'] = False  # 正常显示负号
​
import pandas as pd
import os
​
os.chdir(r'D:\CodeProject\03data_processing_analysis\my_project')
os.getcwd()

状态接口

步骤:

1. 准备x轴和y轴的数据

2. 创建画布: plt.figure(figsize=(画布大小)). figure: 创建画布, figsize: 指定画布大小

3. 绘图, 传入x轴和y轴数据: plt.plot(x, y)

4. 设置x轴和y轴坐标及范围: plt.xlim(0, 10), plt.xlim(0, 10)

5. 设置网格: plt.grid(True)

6. 设置x轴和y轴的标签: plt.xlabel('标签内容', size=大小(数字))

   plt.xlabel('标签内容', size=大小(数字))

7. 设置标题: plt.title('内容', size=大小(数字))

8. 具体显示绘图结果: plt.show()

代码:

# 准备x轴和y轴的一些坐标点, 结合x, y轴就可以确定一个点的位置
x = [1, 3, 2, -1]
y = [3, 11, 8, 3]
​
# 创建1个画板
plt.figure(figsize=(12, 6))
​
# 开始绘图
plt.plot(x, y)
​
# 设置坐标值的范围
plt.xlim(-1, 3)
plt.ylim(0, 11)
​
# 设置网格
plt.grid(True)
​
# 设置x和y轴标签
plt.xlabel('x轴')
plt.ylabel('y轴')
​
# 设置标题
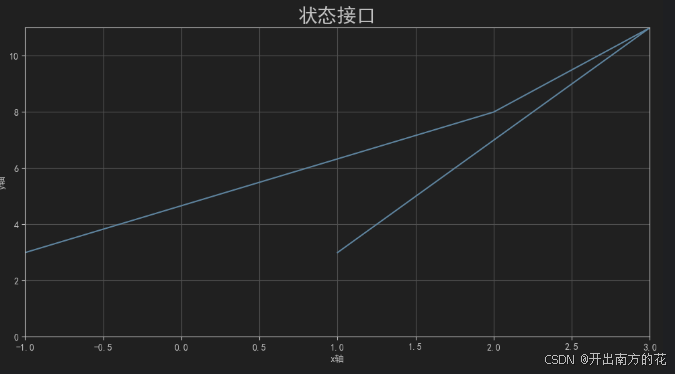
plt.title('状态接口', fontsize=21)
​
# 具体绘图动作
plt.show()

结果图

面向对象

步骤:

1. 准备x轴 和 y轴的一些坐标点, 结合x, y轴就可以锁定1个点的位置.

2. 创建画布和坐标对象: fig, ax = plt.subplots(figsize=(范围))

3. 利用坐标对象开始绘图: ax.plot(x, y)

4. 设置坐标值的范围: ax.set_xlim(范围), ax.set_ylim(范围)

5. 设置网格: ax.grid(True)

6. 设置x轴和y轴坐标: ax.set_xlabel('x轴'), ax.set_xlabel('x轴')

7. 设置标题: ax.set_title('内容')

8. 具体绘图结果: plt.show()

代码:

# 主备x轴和y轴的一些坐标点, 结合x, y轴就可以确定一个点的位置
x = [1, 3, 2, -1]
y = [3, 11, 8, 3]
​
# 调用函数, 创建1个画板, 及坐标对象
fig, ax = plt.subplots(figsize=(12, 6))
​
# 开始绘图
ax.plot(x, y)
​
# 设置坐标值的范围
ax.set_xlim(-1, 3)
ax.set_ylim(0, 11)
​
# 设置网格
ax.grid(True)
​
# 设置x和y轴标签
ax.set_xlabel('x轴')
ax.set_ylabel('y轴')
​
# 设置标题
ax.set_title('状态接口', fontsize=21)
​
# 具体绘图动作
plt.show()

结果图

散点图-可视化重要性

数据集介绍

1. 通过Anscombe数据集说明数据可视化的重要性

2. Anscombe数据集由英国统计学家Frank Anscombe创建

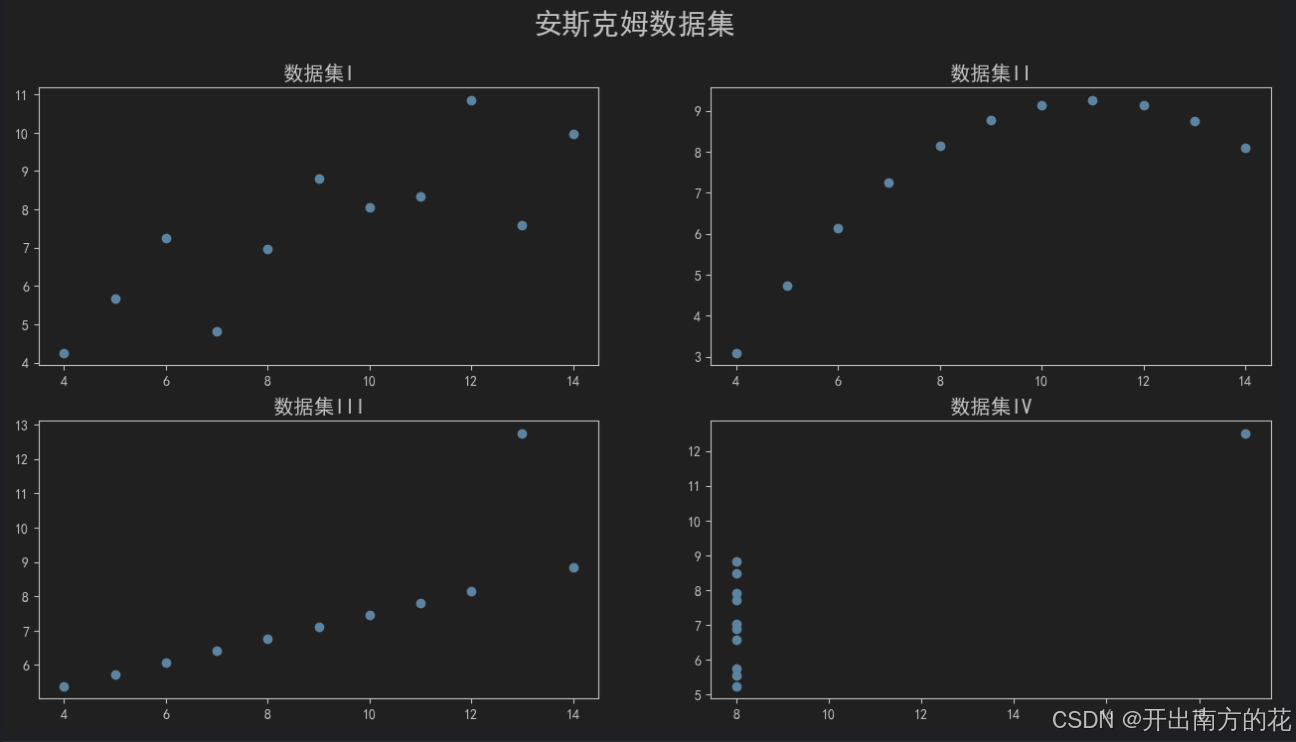
3. 数据集包含4组数据，每组数据包含两个连续变量。

4. 每组数据的平均值、方差、相关性基本相同，但是当它们可视化后，就会发现每组数据的模式明显不同。

describe()查看数据的查看数据的分布情况

发现每组数据中, x, y 的分布情况基本相同, 从均值, 极值和几个4分位数上看, 这几组数据貌似分布差不多

anscombe = pd.read_csv('data/anscombe.csv')
anscombe
​
anscombe.describe()
anscombe[anscombe.dataset == 'I'].describe()
anscombe[anscombe.dataset == 'II'].describe()
anscombe[anscombe.dataset == 'III'].describe()
anscombe[anscombe.dataset == 'IV'].describe()
​
# 上述格式的合并版, 按照 dataset进行分组, 然后统计.
anscombe.groupby('dataset').describe().T  # 转置矩阵
anscombe.groupby('dataset').describe().T

代码-数据可视化

# 可视化
# 获取画布对象
fig = plt.figure(figsize=(16, 8))
​
# 获取坐标轴对象
# 2行2列, 对应坐标轴1, 即: 第1个位置. 
ax1 = fig.add_subplot(2, 2, 1)
# 2行2列, 对应坐标轴2, 即: 第2个位置. 
ax2 = fig.add_subplot(2, 2, 2)
# 2行2列, 对应坐标轴3, 即: 第3个位置. 
ax3 = fig.add_subplot(2, 2, 3)
# 2行2列, 对应坐标轴4, 即: 第4个位置. 
ax4 = fig.add_subplot(2, 2, 4)
​
# 绘制散点图的过程
# 下述两种写法效果一致
ax1.scatter(anscombe[anscombe.dataset == 'I'].x, anscombe[anscombe.dataset == 'I'].y)
ax2.scatter(anscombe[anscombe.dataset == 'II'].x, anscombe[anscombe.dataset == 'II'].y)
ax3.scatter(anscombe.query("dataset == 'III'").x, anscombe.query("dataset == 'III'").y)
ax4.scatter(anscombe.query("dataset == 'IV'").x, anscombe.query("dataset == 'IV'").y)
​
# 设置标题
# 子集
ax1.set_title('数据集I', fontsize=15)
ax2.set_title('数据集II', fontsize=15)
ax3.set_title('数据集III', fontsize=15)
ax4.set_title('数据集IV', fontsize=15)
# 画布标题
fig.suptitle('安斯克姆数据集', fontsize=21)
​
# 具体绘图过程
plt.show()

结果图

单变量直方图

格式

df对象/plt.hist(total_bill, bins)

total_bill: 表示要绘制的列

bins: 分成几个区间(底层是等差数列)

等差数列(分成10个区间需要11个值), 生成3.07 ~ 50.81区间的11个等差数列

np.linspace(3.07, 50.81, 11)

直方图的高度, 就是落到每个区间中的数据的条目数

代码

tips = pd.read_csv('data/tips.csv')
tips
​
tips.describe()  # total_bill: 最小值:3.070000, 最大值: 50.810000
​
# 绘制直方图
# hist(): total_bill: 表示要绘制的列,  bins: 分成几个区间(底层是等差数列)
# 等差数列(分成10个区间需要11个值)
# 生成3.07 ~ 50.81区间的11个等差数列
# np.linspace(3.07, 50.81, 11)
​
# pandas写法
# tips.hist('total_bill', bins=10, figsize=(16, 8))
​
# Matplotlib写法
plt.hist(tips.total_bill, bins=10)
plt.xlabel('消费金额')
plt.ylabel('频次')
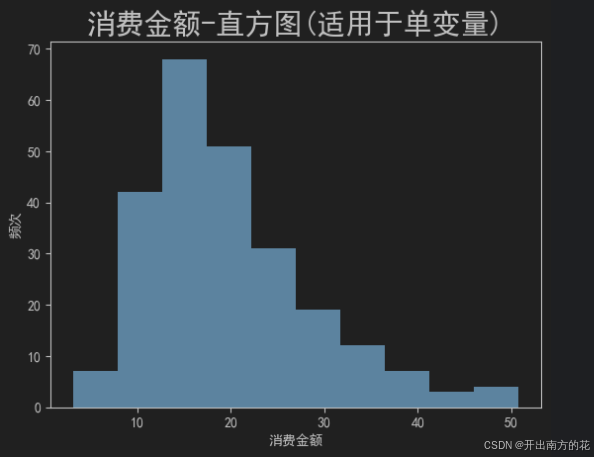
plt.title('消费金额-直方图(适用于单变量)', fontsize=21)
plt.show()

结果图

双变量散点图

概述

1. 双变量（bivariate)指两个变量

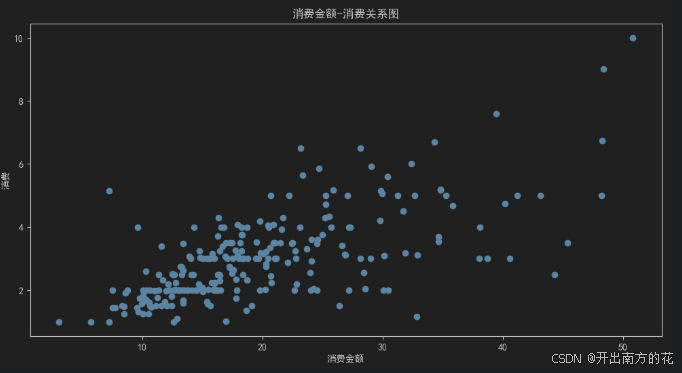
2. 散点图用于表示一个连续变量随另一个连续变量的变化所呈现的大致趋势

3. 例如: 了解账单金额和小费之间的关系可以绘制散点图

代码

# 画布
plt.figure(figsize=(12, 6))
# 绘制散点图
plt.scatter(tips.total_bill, tips.tip)
# 横纵坐标
plt.xlabel('消费金额')
plt.ylabel('消费')
# 设置标题
plt.title('消费金额-消费关系图')
# 具体画图
plt.show()

结果图

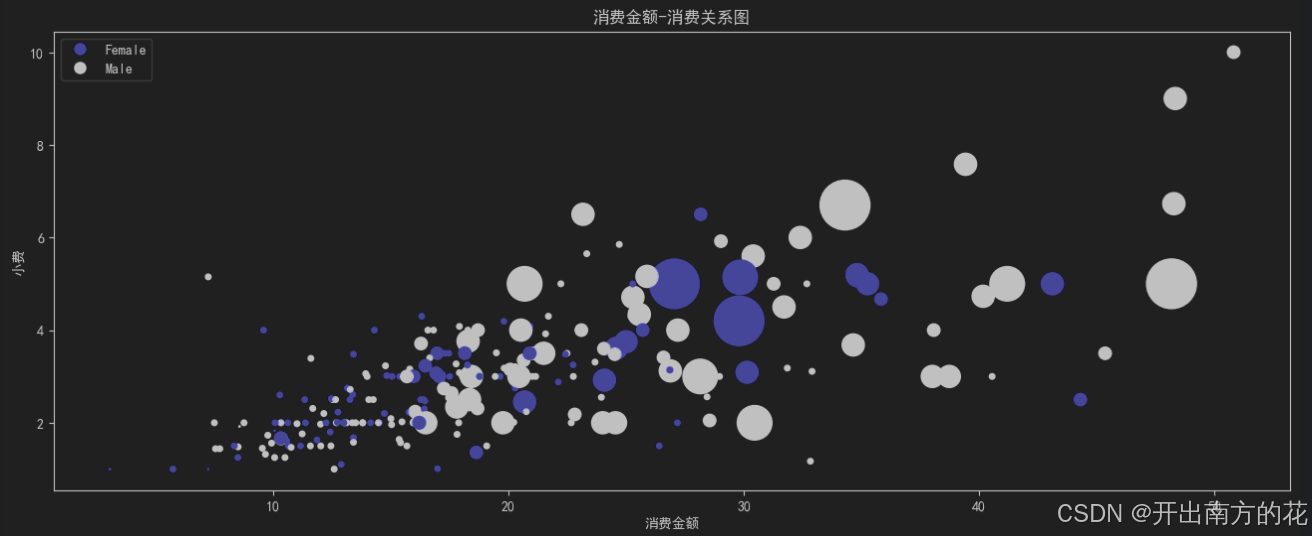
多变量散点图

概述

1. 在散点图的基础上, 可以通过颜色来区分不同的类别

2. 散点的大小也可以用来表示一个变量

代码

# 在上述基础上, 增加性别信息
tips
​
# 给原始数据增加一列, 根据性别显示颜色
tips['sex_color'] = tips.sex.apply(lambda sex: 'blue' if sex == 'Female' else 'black')
tips
​
# 绘图
plt.figure(figsize=(16, 6))
plt.scatter(tips.total_bill, tips.tip, c=tips.sex_color, alpha=1,
            s=tips['size'] * tips['size'] * tips['size'] * tips['size'])
# 横纵坐标
plt.xlabel('消费金额')
plt.ylabel('小费')
​
# 设置图例
from matplotlib.lines import Line2D
legend_elements = [Line2D([0], [0], marker='o', color='w', label='Female', 
                            markerfacecolor='blue', markersize=10),
                   Line2D([0], [0], marker='o', color='w', label='Male', 
                            markerfacecolor='black', markersize=10)]
​
plt.legend(handles=legend_elements)
​
# 设置标题
plt.title('消费金额-消费关系图')
# 具体画图
plt.show()

结果图