动态规划day38|322. 零钱兑换(背包满了吗?最小值怎么表示?)、279. 完全平方数、139. 单词拆分、多重背包要点、背包问题大总结
动态规划day38|322. 零钱兑换(背包满了吗?最小值怎么表示?)、279. 完全平方数、139. 单词拆分、多重背包要点、背包问题大总结
- 322. 零钱兑换
- 279. 完全平方数
- 139. 单词拆分
- 多重背包要点
- 背包问题大总结
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
第一次做的时候,我不知道该怎么去表示背包已经满了以及什么才是最小值
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount+1,INT_MAX);
dp[0]=0;
for(int i=0;i<coins.size();i++)
for(int j=coins[i];j<=amount;j++)
if(dp[j-coins[i]]!=INT_MAX)
dp[j]=min(dp[j-coins[i]]+1,dp[j]);
if(dp[amount]==INT_MAX) return -1;
return dp[amount];
}
};
首先回答我一开始的两个疑问:
- 怎么去表示背包已经满了?
首先我们整体过一遍背包的过程:对于第一个物品,从dp[coins[i]]开始,它是在dp[0]的基础上加的,所以它必然是满的,然后之后一个背包就是在dp[coins[i]]的基础上加的,所以它也是满的……就这样不断迭代推进,像多米诺骨牌一样,要不就装不了,要不就是装满的。如果从中间看确实难看出来,但是从开头的几个,如当i=0时的dp[1]、dp[2],就明确的知道:只要dp[j]有值,那么它就是满的 - 什么才是最小值?
这就是递归函数的作用,一般最大值要有max,最小值要有min,求个数问题则是求和。
为什么这样(dp[j]=min(dp[j-coins[i]]+1,dp[j])) 就是最小值?我们还是一样,从开头开始看,当新物品纳入的时候,我们就要考虑是加入新物品“好”,还是不加新物品“好”,每回都是选两者中最小的,那么到了后面,自然而然就是最小值了。
易错点:
- 初始化:由于是求min,所以必须初始化为INT_MAX,绝不能简单的赋为0,否则0会覆盖真正的值。
if(dp[j-coins[i]]!=INT_MAX)
dp[j]=min(dp[j-coins[i]]+1,dp[j]);
这里的if条件不可少,如果没有它,那么dp[j-coins[i]]+1就会超过INT_MAX,从而引发异常
if(dp[amount]==INT_MAX) return -1;
当不能凑出amout的时候,dp[amount]的值还是原来初始化的值。至于为什么,你可以借助开头的几个dp来理解。
279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
提示:
1 <= n <= 104
class Solution {
public:
vector<int> pingFangShu(int n)
{
vector<int> nums(n);
for(int i=1;;i++)
{
if(i*i<=n)
nums.push_back(i*i);
else
break;
}
return nums;
}
int numSquares(int n) {
vector<int> dp(n+1,INT_MAX);
dp[0]=0;
vector<int> nums=pingFangShu(n);
for(int i=0;i<nums.size();i++)
for(int j=nums[i];j<=n;j++)
if(dp[j-nums[i]]!=INT_MAX)
dp[j]=min(dp[j-nums[i]]+1,dp[j]);
return dp[n];
}
};
这样的写法是可以的,但是超出了力扣的时间限制。上面的是单独生成“物品”,选择只好在for循环里面边遍历边生成了,代码如下:
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n+1,INT_MAX);
dp[0]=0;
for(int i=1;i*i<=n;i++)
for(int j=i*i;j<=n;j++)
if(dp[j-i*i]!=INT_MAX)
dp[j]=min(dp[j-i*i]+1,dp[j]);
return dp[n];
}
};
原理和322基本相同。
139. 单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
**注意:**不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。
示例 2:
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意,你可以重复使用字典中的单词。
示例 3:
输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false
提示:
1 <= s.length <= 3001 <= wordDict.length <= 10001 <= wordDict[i].length <= 20s和wordDict[i]仅由小写英文字母组成wordDict中的所有字符串 互不相同
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
vector<bool> dp(s.size() + 1, false);
dp[0] = true;
for (int j = 1; j <= s.size(); j++) { // 遍历背包
for (int i = 0; i < j; i++) { // 遍历物品
string word = s.substr(i, j - i); //substr(起始位置,截取的个数)
if (wordSet.find(word) != wordSet.end() && dp[i]) {
dp[j] = true;
}
}
}
return dp[s.size()];
}
};
本题难度较高,一刷可放过
多重背包要点
- 有N种物品和一个容量为W 的背包。第 i 种物品最多有 Mi 件可用,每件耗费的空间是Ci ,价值是 Vi ,求价值总和最大。
- **多重背包和01背包是非常像的:**每件物品最多有Mi件可用,把Mi件摊开,其实就是一个01背包问题了,即:
for (int i = 0; i < n; i++) {
while (nums[i] > 1) { // 物品数量不是一的,都展开
weight.push_back(weight[i]);
value.push_back(value[i]);
nums[i]--;
}
}
vector<int> dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // 遍历物品,注意此时的物品数量不是n
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
return dp[bagWeight]
}
- 多重背包在面试中基本不会出现
背包问题大总结
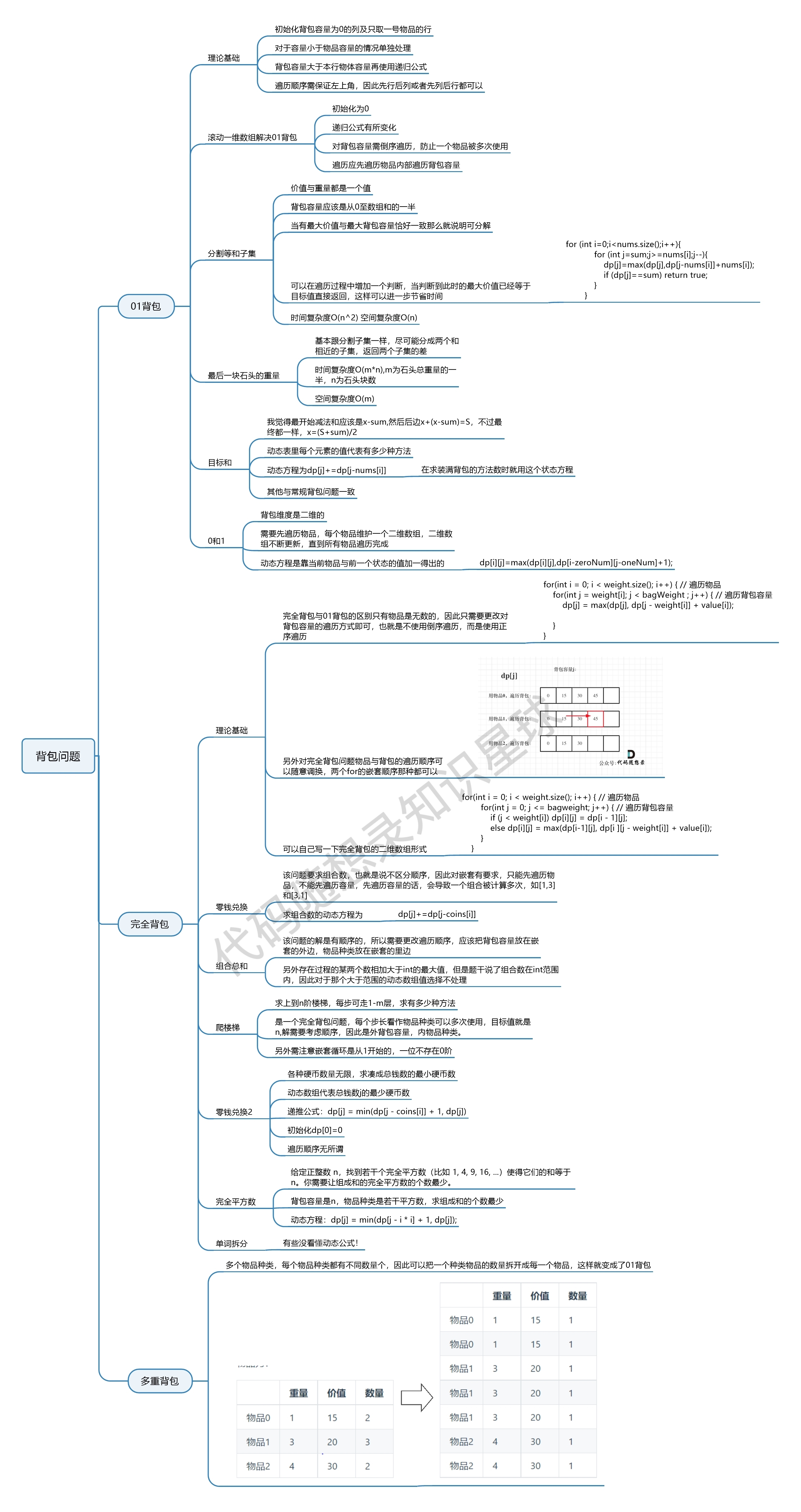
(这个图是代码随想录知识星球成员海螺人所画)
