当前位置：首页 > article >正文

LeetCode题练习与总结：搜索二维矩阵 Ⅱ--240

article 2024/11/17 3:40:00

一、题目描述

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例 1：

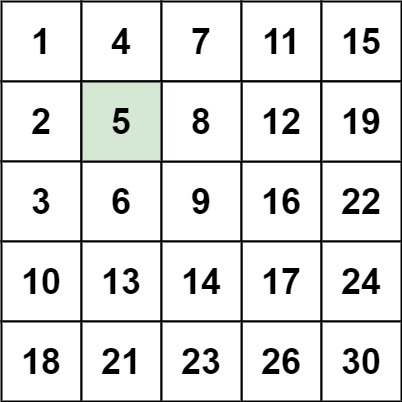
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：

m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-10^9 <= matrix[i][j] <= 10^9
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-10^9 <= target <= 10^9

二、解题思路

由于矩阵的每行和每列都是有序的，我们可以利用这一特性来提高搜索的效率。一个有效的策略是从矩阵的右上角开始搜索：

如果当前位置的元素等于目标值，则返回 true。
如果当前位置的元素大于目标值，则向左移动（即列索引减一），因为当前列的其它元素都会大于目标值。
如果当前位置的元素小于目标值，则向下移动（即行索引加一），因为当前行的其它元素都会小于目标值。
如果移动超出了矩阵的边界，则返回 false。

三、具体代码

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        // 从矩阵的右上角开始搜索
        int row = 0;
        int col = matrix[0].length - 1;

        // 当行索引在矩阵范围内时进行搜索
        while (row < matrix.length && col >= 0) {
            if (matrix[row][col] == target) {
                // 找到目标值，返回 true
                return true;
            } else if (matrix[row][col] > target) {
                // 当前值大于目标值，向左移动
                col--;
            } else {
                // 当前值小于目标值，向下移动
                row++;
            }
        }

        // 没有找到目标值，返回 false
        return false;
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

定义：时间复杂度是指算法执行的操作数量与输入数据量之间的关系。
分析：
- 矩阵的行数为 m，列数为 n。
- 在最坏的情况下，算法可能需要遍历矩阵的一行或一列，即最多需要遍历 m + n 个元素。
- 在每一步中，算法要么向下移动一行，要么向左移动一列，因此每一步都会排除一行或一列。
结论：时间复杂度为 O(m + n)，其中 m 是矩阵的行数，n 是矩阵的列数。

2. 空间复杂度

定义：空间复杂度是指算法执行过程中临时占用存储空间的大小。
分析：
- 算法使用了常数个额外空间，即 row 和 col 两个变量来记录当前搜索的位置。
- 矩阵本身的空间不计入算法的空间复杂度，因为题目假设输入矩阵已经存在。
结论：空间复杂度为 O(1)，因为算法使用的额外空间不随输入数据的大小而变化。

五、总结知识点

二维数组：
- int[][] matrix：表示一个二维整型数组，用于存储矩阵数据。
变量声明和初始化：
- int row = 0;：声明并初始化一个整型变量 row，用于表示矩阵的行索引。
- int col = matrix[0].length - 1;：声明并初始化一个整型变量 col，用于表示矩阵的列索引，并初始化为最后一列。
循环结构：
- while (row < matrix.length && col >= 0)：使用 while 循环来重复搜索过程，直到行索引超出矩阵的行数范围或列索引小于 0。
条件判断：
- if (matrix[row][col] == target)：判断当前元素是否等于目标值。
- else if (matrix[row][col] > target)：判断当前元素是否大于目标值。
- else：处理以上条件都不满足的情况。
数组元素访问：
- matrix[row][col]：通过行索引和列索引访问矩阵中的元素。
控制流：
- col--;：减少列索引，表示向左移动。
- row++;：增加行索引，表示向下移动。