Unity中的功能解释(数学位置相关和事件)

向量计算

Vector3.Slerp（起点坐标，终点坐标，t），可是从起点坐标以一个圆形轨迹到终点坐标，有那么多条轨迹，那怎么办

Vector3.Slerp 进行的是沿球面插值，因此并不是沿着严格的“圆形轨迹”移动，而是在两点所在的大圆弧（球体上的最短路径）上插值。

点乘叉乘判断方位，点乘得到的结果大于0和小于0，大于0的时候相距的角度大于90度，小于0则说明在前方

90度以内为正，到180为负，此为两向量点乘可得结果

所以两点之间可以判断前后的关系

叉乘，两向量相乘出垂直的向量，通过新向量的.y判断左右，大于0朝上，说明在目标向量的右侧，小于0，说明在目标向量的左侧

点乘（Dot Product）

A⋅B=∣A∣∣B∣cosθ

A⋅B=A1​B1​+A2​B2​+⋯+An​Bn​

• 2D 点乘： 若 A=(Ax,Ay)\mathbf{A} = (A_x, A_y)A=(Ax​,Ay​) 和 B=(Bx,By)\mathbf{B} = (B_x, B_y)B=(Bx​,By​)，那么点乘为：

  A⋅B=AxBx+AyBy\mathbf{A} \cdot \mathbf{B} = A_x B_x + A_y B_yA⋅B=Ax​Bx​+Ay​By​

• 3D 点乘： 若 A=(Ax,Ay,Az)\mathbf{A} = (A_x, A_y, A_z)A=(Ax​,Ay​,Az​) 和 B=(Bx,By,Bz)\mathbf{B} = (B_x, B_y, B_z)B=(Bx​,By​,Bz​)，那么点乘为：

  A⋅B=AxBx+AyBy+AzBz\mathbf{A} \cdot \mathbf{B} = A_x B_x + A_y B_y + A_z B_zA⋅B=Ax​Bx​+Ay​By​+Az​Bz​

debug的射线

Debug.DrawLine（点&点）

Debug.DrawLine(Vector3 start, Vector3 end, Color color, float duration);

Vector3 startPoint = new Vector3(0, 0, 0);
Vector3 endPoint = new Vector3(5, 0, 0);
Debug.DrawLine(startPoint, endPoint, Color.red, 2.0f); 
 // 画一条从 (0,0,0) 到 (5,0,0) 的红色线，持续2秒

Debug.DrawRay （点&向量）

Debug.DrawRay(Vector3 start, Vector3 direction, Color color, float duration);

Vector3 rayOrigin = new Vector3(0, 0, 0);
Vector3 rayDirection = new Vector3(5, 0, 0);  // 方向向量控制长度
Debug.DrawRay(rayOrigin, rayDirection, Color.blue, 2.0f);
  // 画出长度为 5 的蓝色射线，持续2秒

Camera的坐标系转换

• WorldToScreenPoint: 将世界坐标转换为屏幕坐标。常用于把场景中物体的位置转换为 UI 屏幕上的坐标。

• 物体位置转为 UI 坐标：假设你有一个 3D 物体，你希望在 UI 上显示其位置，或者让一个 UI 元素跟随它。这时你就需要把物体的世界坐标转换为屏幕坐标，UI 系统才能正确定位该元素。

• 射线检测或点击交互：你可以使用 WorldToScreenPoint 来将 3D 世界中的物体位置转换为 2D 坐标，以便处理基于屏幕点击的交互，例如在物体上点击时触发某些事件。

• // 获取物体的世界坐标
  Vector3 worldPosition = objectTransform.position;
  
  // 将世界坐标转换为屏幕坐标
  Vector3 screenPosition = Camera.main.WorldToScreenPoint(worldPosition);
  
  // 现在 screenPosition 包含物体在屏幕上的 X、Y 坐标（以像素为单位），和 Z 值（深度）。

  关于Z值：是目标点，垂直到相机面的距离。

• Z 值可以用来判断物体是在摄像机的前面（正值）还是后面（负值）

• ScreenToWorldPoint: 将本地屏幕坐标转换为世界坐标。通常在基于屏幕点击（例如鼠标点击）来确定场景中的具体位置时使用。

• // 获取鼠标点击位置（屏幕坐标）
  Vector3 screenPosition = Input.mousePosition;
  
  // 设置一个距离（深度值）
  screenPosition.z = 10.0f; // 假设距离摄像机10个单位
  
  // 将屏幕坐标转换为世界坐标
  Vector3 worldPosition = Camera.main.ScreenToWorldPoint(screenPosition);
  
  // 使用 worldPosition 在3D世界中做某些操作，比如放置物体
  

• Z 值的作用：ScreenToWorldPoint 的 Z 值非常重要。它决定了转换的深度，即这个屏幕坐标在 3D 世界中距离摄像机有多远。如果 Z 值太小，结果会在摄像机附近；如果 Z 值太大，结果会在远处的世界位置。ScreenToWorldPoint 用来将屏幕上的 2D 坐标转换为 3D 世界中的点，核心是需要一个 Z 值来确定该点在世界中的深度位置。

• WorldToViewportPoint: 将世界坐标转换为视口坐标。视口坐标通常指的是 (0,0) 到 (1,1) 范围内的相对坐标，常用于与 UI 元素的交互。

• // 获取物体的世界坐标
  Vector3 worldPosition = objectTransform.position;
  
  // 将世界坐标转换为视口坐标
  Vector3 viewportPosition = Camera.main.WorldToViewportPoint(worldPosition);
  
  // 现在 viewportPosition 是 (X, Y, Z) 值
  // X 和 Y 值的范围为 0 到 1，表示相对摄像机视野中的位置
  // Z 值表示物体与摄像机之间的距离
  

  视口坐标的 X 和 Y 值可以超出 0 到 1 的范围

• 这些坐标值是相对的，X 和 Y 超出范围并不意味着物体完全不可见，物体仍然可能部分显示在边缘（视角的原因）。

• 如果物体的视口坐标的 X 和 Y 值在 (0,0) 到 (1,1) 之间，并且 Z 值为正，则物体在摄像机的视野内；否则物体在视野外或被其他物体遮挡。

• ViewportToWorldPoint: 将视口坐标转换为世界坐标。这在处理以视口为基础的坐标系转换时很有用，比如在分辨率变化时保持特定 UI 元素的比例。

• ViewportToScreenPoint: 将视口坐标转换为屏幕坐标。可以帮助从相对的视口坐标系转换到具体像素的屏幕坐标系。

• 视口坐标系：这是相对的，(0,0) 代表左下角，(1,1) 代表右上角，与屏幕的分辨率无关。
• 屏幕坐标系：这是绝对的，单位是像素。例如，在 1920x1080 的屏幕上，(1920,1080) 代表屏幕的右上角。

• 视口超出 0 到 1 的范围：如果视口坐标的 X 和 Y 值超出了 (0,0) 到 (1,1)，那么屏幕坐标也会相应地超出屏幕范围，代表物体在屏幕之外。

Transform的坐标系方法

Transform 有父物体时，transform.position 表示的是该物体在世界坐标系中的位置

（注：这里的本地，指的是每一个transform组件，都有自己的本地坐标系）

世界转本地

传入世界vector3，然后以本物体的坐标系重新修改，再返回改后 的vector3

• InverseTransformDirection：将一个方向向量从世界空间转换到本地空间（即局部空间）。这个向量表示的是一个方向，不会受到位移的影响。
• InverseTransformPoint：将一个点的坐标从世界空间转换到本地空间。这个方法会受到父对象的位置影响。
• InverseTransformVector：将一个向量从世界空间转换到本地空间。和 InverseTransformDirection 类似，但它不仅仅表示方向，还可以包括缩放。
• 为毛偏用inverse："inverse" 通常给人一种“反转”的感觉，但在这里的语境中，它指的是 从世界坐标系 “逆转回”到局部坐标系 的操作。
• 这个“Inverse” 其实指的是矩阵的逆变换。在 3D 渲染或游戏开发中，Transform 操作本质上是通过矩阵来进行坐标转换的。对象在世界坐标系中的变换（位置、旋转、缩放）会组成一个变换矩阵，这个矩阵可以把局部坐标转换到世界坐标系。而“逆矩阵”操作则是反过来，将世界坐标系的值转换回局部坐标系。

本地坐标转世界坐标：

Vector3 localDirection = new Vector3(1, 0, 0); // 本地坐标中的向右方向
Vector3 worldDirection = transform.TransformDirection(localDirection); // 转换为世界坐标系的方向

 本transform下的坐标传入，转为世界的坐标

• TransformDirection：将一个本地坐标系下的方向转换到世界坐标系。
• TransformPoint：将一个本地坐标系下的点的坐标转换到世界坐标系。
• TransformVector：将一个本地坐标系下的向量转换到世界坐标系。

// 获取物体的 Transform 组件
Transform objTransform = gameObject.transform;

// 使用 TransformPoint 方法将本地坐标转换为世界坐标
Vector3 worldPosition = objTransform.TransformPoint(localPosition);

// 使用 InverseTransformPoint 方法将世界坐标转换为本地坐标
Vector3 localPosition = objTransform.InverseTransformPoint(worldPosition);

 意思是一个Transform，的坐标值，会因为父对象改变而改变，并不完全取决于世界坐标

一个对象的 Transform 通常包括位置（position）、旋转（rotation）和缩放（scale）等属性。

这些属性的值可以分为局部坐标（local coordinates）和世界坐标（world coordinates）两种，五五开。

弧度数值与角度数值

rad弧度。degree角度

角度乘以一个0.几转换成弧度

弧度乘以五十多变成角度

Mathf.Lerp

public static float Lerp(float a, float b, float t);

• a：起始值。
• b：结束值。
• t：插值因子，取值范围通常为 [0, 1]。当 t=0 时返回 a，当 t=1 时返回 b，如果 t 在 0 和 1 之间，返回 a 和 b 之间的线性插值值。

工作原理：

Lerp 函数的原理是：

result=a+(b−a)×t

当 t 为 0 时，结果是 a；当 t 为 1 时，结果是 b；而 t 为 0 和 1 之间的值时，结果是 a 和 b 之间的插值。

BaseEventData

• 统一处理不同事件类型的数据：

  • 不同的事件（如鼠标点击、键盘按键、触摸、拖拽）可能需要传递不同的信息。eventData 通过不同的子类（如 PointerEventData、AxisEventData）来封装这些信息，简化了事件系统的处理流程。
  • 这样，所有事件的数据结构就变得一致，方便事件的处理和扩展。

• 传递事件的详细信息：

  • 当你处理用户交互时，除了知道事件发生了之外，通常你还需要了解事件发生的具体细节。例如：
    • 用户点击了什么位置？
    • 用户拖拽了哪个对象？
    • 鼠标或触控设备按下的是哪个按钮？
  • eventData 中包含了这些信息，可以让你在事件回调中轻松获取并处理这些数据。

举例说明：

假设你在处理点击事件时，如果只提供一个简单的事件通知，可能只能知道“某个按钮被点击了”。但使用 PointerEventData，你可以得到更多的信息：

• 点击的对象是什么。
• 点击的坐标是哪里。
• 按下的鼠标按钮是哪一个（左键、右键、中键等）。
• 是否发生了拖拽操作。

• public void OnButtonClick(PointerEventData eventData)
  {
      Debug.Log("Clicked at position: " + eventData.position);
  }

ugui的RectTransform

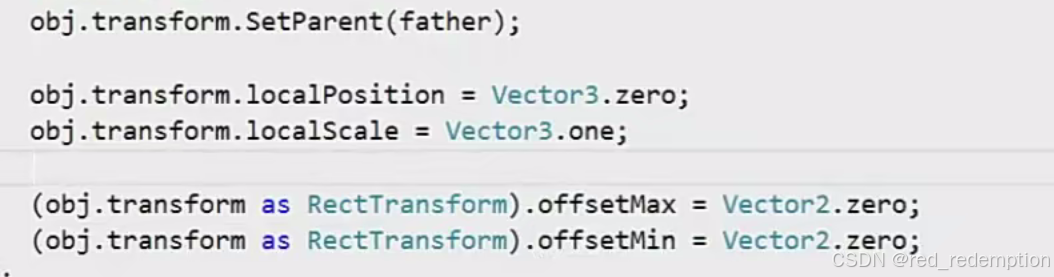
unity中的小碎块功能

ugui不允许在同一个物体上挂相同的组件

lambda表达式的简写

（）=>{        }

单个参数，且已知类型，可以省括号

仅一条返回语句，不用写return，直接在=>右边写要返回的东西

错误示例：

错误  Func<int> func = () => return 1；
正确  Func<int> func = () => 1;  // 简写形式，无需 return 关键字
正确  Func<int> func = () =>{  return 1; };// 显式使用 return 关键字

只有一个参数的 Lambda 表达式

单行表达式: 如果 lambda 表达式仅包含一个表达式，可以省略花括号和 return 关键字

x => x * x 表示一个接受一个参数 x 并返回 x * x

Func<int, int> square = x => x * x;

 多个参数的 Lambda 表达式

(x, y) => x + y 表示一个接受两个参数 x 和 y 并返回它们的和

Func<int, int, int> add = (x, y) => x + y;

 无参数的 Lambda 表达式

不接受参数并执行 Console.WriteLine("Hello, World!")

Action greet = () => Console.WriteLine("Hello, World!");

 块状的 Lambda 表达式

单个参数配块状代码

Func<int, int> doubleValue = x =>
{
    int result = x * 2;
    return result;
};

 类型推断与显式类型

编译器可以自动推断 lambda 表达式的参数类型

Func<int, int> increment = x => x + 1;  // 自动推断参数类型为 int

你也可以显式指定参数类型（通常在委托声明时指定）

Func<int, int> increment = (int x) => x + 1;

Resources.Load<T>()

Resources.LoadAsync<T>()

返回值的问题

这两种泛型资源加载都只有一种返回值，Load是返回T，Loadasync返回ResourceRequest，T在ResourceRequest.asset中体现

Resources.Load<T>():

• 这个方法会立即加载资源，并返回你指定类型 T 的对象。
• 你需要手动指定资源的类型，通过泛型参数 T。返回值的类型就是你传入的 T。
• Resources.Load() 还有非泛型的重载，返回值类型是 UnityEngine.Object

Resources.LoadAsync<T>():

• 这个方法是异步加载资源。加载过程不会阻塞主线程，返回的对象是一个 ResourceRequest，但是其中包含你指定的泛型类型 T。
• 加载完成后，你可以通过 ResourceRequest.asset 访问加载的资源，该资源类型是你指定的 T。

泛型的问题

总结：泛型是要自己输入的，用泛型T是为了减少手动类型转换的过程

如果不传入泛型 T，Resources.Load() 会返回一个通用的 UnityEngine.Object

必须手动将它转换为你期望的类型

Object obj = Resources.Load("MyPrefab");  // 返回 UnityEngine.Object
GameObject myPrefab = (GameObject)obj;    // 手动转换

if (obj is GameObject)
{
    GameObject myPrefab = (GameObject)obj;
}

GameObject myPrefab = Resources.Load<GameObject>("MyPrefab");

所以泛型T，要手动传入这个资源的类型，从而省去里面的类型转换

如果泛型填的不对，就执行不了

如果你在泛型中传入了错误的类型（比如试图加载一个 AudioClip 但是传入了 GameObject），不会执行成功，返回 null，而不会发生类型转换的错误（InvalidCastException）。这样能在开发过程中帮助你迅速发现错误。

AudioClip audioClip = Resources.Load<AudioClip>("MyPrefab");  // 错误：MyPrefab 不是 AudioClip
if (audioClip == null)
{
    // 资源加载失败，因为资源不是 AudioClip 类型
    Debug.Log("Failed to load AudioClip");
}