[题解] Codeforces Round 976 (Div. 2) A ~ E

签到.

void solve() {
    int n, k;
    cin >> n >> k;
    if (k == 1) {
        cout << n << endl;
        return;
    }
    int ans = 0;
    while (n) {
        ans += n % k;
        n /= k;
    }
    cout << ans << endl;
}

打表发现, 翻转完后的序列为: 011011110111111011111111. 每组 $3,5,7,\mathrm{9...}$ 个数.

直接用等差数列公式求出前缀中 $1$ 的个数, 二分 check 答案

(赛时代码, 也不知道炸不炸 ll, 反正无脑套 __int128)

#define int long long
#define i128 __int128

i128 f(i128 x) { // 求 x 组前缀中 1 的个数
    return ((2 * x + 1) + 3) * x / 2 - x;
}
i128 ff(i128 x) { // 求 x 组前缀中0和1的个数
    return ((2 * x + 1) + 3) * x / 2;
}
int solve(int _) {
    int k; cin >> k;

    i128 l = 0, r = 1e9;
    while (l < r) {
        int mid = (l + r + 1) >> 1;
        if (f(mid) > k)r = mid - 1;
        else if (f(mid) < k)l = mid;
        else return ff(mid);
    }

    return ff(l) + k - f(l) + 1;
}

先列出 a, b, c, d 每 bit 位的运算结果:

eg; fk, 赛时这个表画错了, 半天才发现

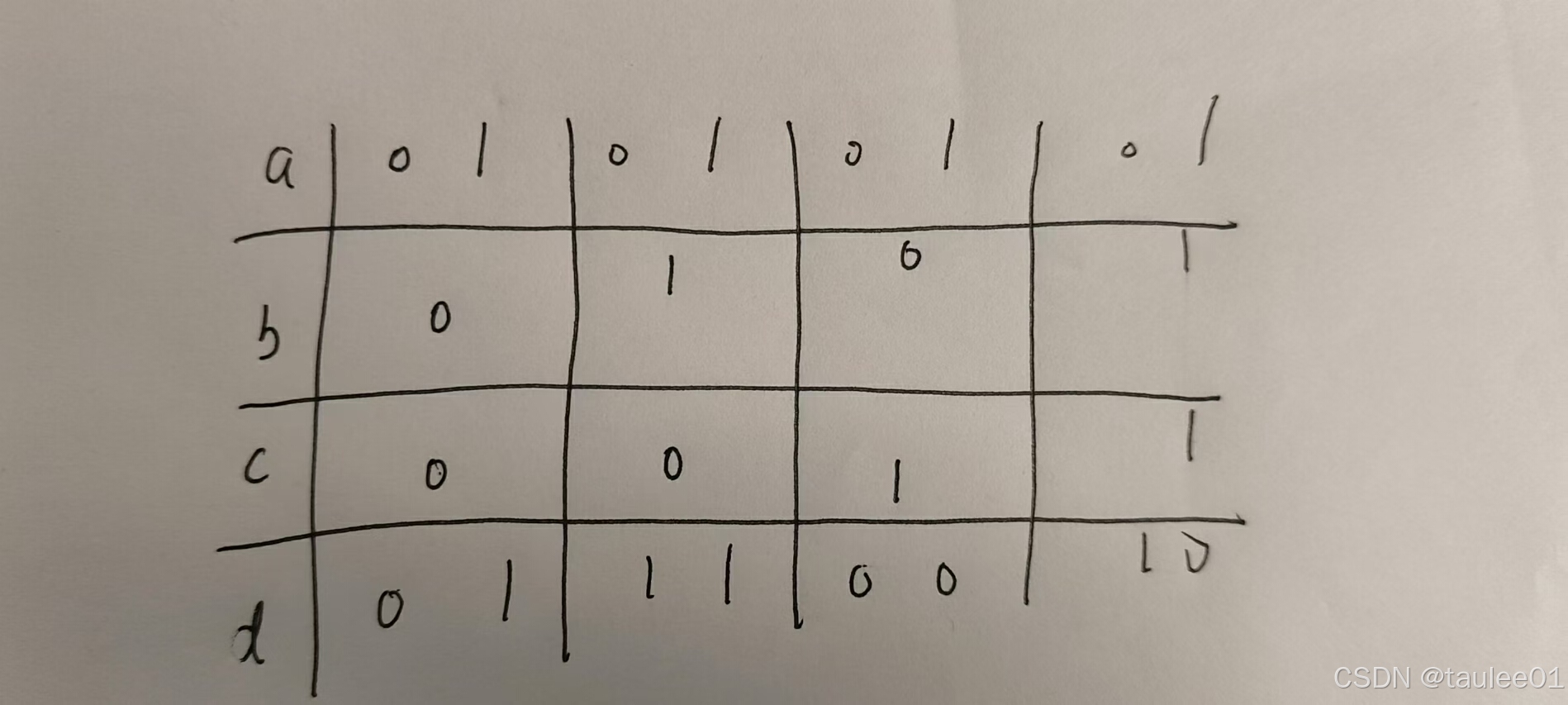
发现, 运算结果不会有负数. 于是每位就自能顾得上自己, 只需要按位检查, 一旦有一位满足不了, 就输出 -1.

#define int long long

bool aa(int x, int i) {return (x >> i) & 1;}
int solve(int _) {
    int a, b, c, d;
    cin >> b >> c >> d;
    a = 0;
    for (int i = 0; i < 61; ++i) {
        if (aa(b, i)) {
            if (aa(c, i)) { //11
                if (!aa(d, i)) {
                    a += 1ll << i;;
                }
            }
            else { // 10
                if (aa(d, i)) {
                    a += 1ll << i;
                }
                else {
                    return -1;
                }
            }
        }
        else {
            if (aa(c, i)) { // 01
                if (aa(d, i)) {
                    return -1;
                }
            }
            else { // 00
                if (aa(d, i)) {
                    a += 1ll << i;
                }
            }
        }
    }
    return a;
}

首先考虑用并查集维护两个点的连通块所属关系. 但是操作太多, 会 tle.

d 最大为 10, 于是对于 a[i], 考虑继承前 10 个节点往后跳跃的情况, 更新到 a[i] 上, 同时继承过来的跳跃次数减一. 这样每个点只用往前跳跃最多 10 次.

int n, m, a, d, k, fa[200010], ma[200010][15];
int find(int x) {
    if (fa[x] == x)return x;
    return fa[x] = find(fa[x]); //并查集路径压缩
}
int solve(int _) {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        fa[i] = i;
        for (int j = 1; j <= 10; ++j) {
            ma[i][j] = 0;
        }
    }

    for (int i = 1; i <= m; ++i) {
        cin >> a >> d >> k;
        ma[a][d] = max(ma[a][d], k);
    }

    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= 10; ++j) {
            if (i - j < 1)break;
            if (ma[i - j][j])fa[find(i)] = find(i - j); //从前面跳过来, 更新一下并查集
        }
        for (int j = 1; j <= 10; ++j) {
            if (ma[i][j] > 1 && i + j <= n)ma[i + j][j] = max(ma[i + j][j], ma[i][j] - 1); //继承全面没跳跃完的 k
        }
    }

    set<int>se;
    for (int i = 1; i <= n; ++i) {
        se.emplace(find(i));
    }

    return se.size();
}

状压 DP.

a 最大为 1023. 故所有数的异或结果最多 0~1023, 共 1024 种状态.

dp[i][j] 表示前 i 位选取某些异或到一起答案是 j 的概率. 就很好转移了. 见代码. 记得滚动数组优化一下空间.

eg: jiangly 的取模机真好用 ! !

eg: 赛后过题真痛苦, 就差几分钟…

//------取模机------//
using i64 = long long;
template<class T>
constexpr T power(T a, i64 b) {
    T res {1};
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
} // 快速幂

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
} // 取模乘

template<i64 P>
struct MInt {
    i64 x;
    constexpr MInt() : x {0} {}
    constexpr MInt(i64 x) : x {norm(x % getMod())} {}

    static i64 Mod;
    constexpr static i64 getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(i64 Mod_) {
        Mod = Mod_;
    }//只有P<=0, setMod才生效
    constexpr i64 norm(i64 x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr i64 val() const {
        return x;
    }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        if (getMod() < (1ULL << 31)) {
            x = x * rhs.x % int(getMod());
        } else {
            x = mul(x, rhs.x, getMod());
        }
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & {
        return *this *= rhs.inv();
    }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
    friend constexpr bool operator<(MInt lhs, MInt rhs) {
        return lhs.val() < rhs.val();
    }
};

template<>
i64 MInt<0>::Mod = 1e9 + 7; //只有P<=0, Mod才生效

constexpr int P = 1e9 + 7; //在这设置要用的模数
using Z = MInt<P>;
//------取模机------//

i64 n, a[200010];
Z dp[2][1024], p[200010];
int solve(int _) {
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    for (int i = 1; i <= n; ++i) {cin >> p[i]; p[i] /= 1e4;}
    Z ans = 0;
    dp[0][0] = 1;
    for (int i = 1; i < 1024; ++i) {
        dp[0][i] = 0;
    }

    for (int i = 1; i <= n; ++i) {
        int tis = i % 2;
        int last = tis ^ 1;
        for (int j = 0; j < 1024; ++j) dp[tis][j] = 0;
        for (int j = 0; j < 1024; ++j) {
            dp[tis][j ^ a[i]] += dp[last][j] * p[i];
            dp[tis][j] += dp[last][j] * (1 - p[i]);
        }
    }

    for (int i = 0; i < 1024; ++i) {
        ans += dp[n % 2][i] * i * i;
    }

    return ans.val();
}