AcWing算法基础课笔记 第一章 基础算法
新星计划-算法赛道 解读 (qq.com)
新星计划-算法赛道 解读
- 学习期间需要做什么
学习算法,然后写文章
每位学员每周需保证更新不少于2篇的原创文章,如果当周少于2篇文章则失去参赛资格;
- 文章内容有什么要求?
因为每个人的情况不同,所以,大家根据自身学习进度 ,只要输出 算法领域相关的文章即可。
可以是以下方式:
1)观看CSDN算法技能树的笔记。【适合学习C++的同学,尤其是4月份蓝桥杯的同学】
算法技能树 (csdn.net)
2)导师准备的相关学习资料。【合适学习java的同学,尤其是4月份蓝桥杯的同学】
蓝桥杯_热爱编程的小白白的博客-CSDN博客
3)观看算法视频的笔记。【适合刚学算法的同学】
【尚硅谷】数据结构与算法(Java数据结构与算法)_哔哩哔哩_bilibili
数据结构与算法基础(青岛大学-王卓)_哔哩哔哩_bilibili
4)算法题目的解题思路。
题库 - 力扣 (LeetCode) 全球极客挚爱的技术成长平台
下课后背过算法模版,碰到题目要求可以默写的出来
一道题目可以尝试着重复去打个3~5遍以用来去记住模版
作者:yxc
链接:https://www.acwing.com/blog/content/277/
来源:AcWing
目录
编辑快速排序算法模板 —— 模板题 AcWing 785. 快速排序
归并排序算法模板 —— 模板题 AcWing 787. 归并排序
整数二分算法模板 —— 模板题 AcWing 789. 数的范围
浮点数二分算法模板 —— 模板题 AcWing 790. 数的三次方根
高精度加法 —— 模板题 AcWing 791. 高精度加法
高精度减法 —— 模板题 AcWing 792. 高精度减法
高精度乘低精度 —— 模板题 AcWing 793. 高精度乘法
高精度除以低精度 —— 模板题 AcWing 794. 高精度除法
一维前缀和 —— 模板题 AcWing 795. 前缀和
二维前缀和 —— 模板题 AcWing 796. 子矩阵的和
双指针算法 —— 模板题 AcWIng 799. 最长连续不重复子序列, AcWing 800. 数组元素的目标和
区间合并 —— 模板题 AcWing 803. 区间合并

快速排序算法模板 —— 模板题 AcWing 785. 快速排序
分治的思想 (先分完再去递归两边)

较为粗暴:

优雅:
利用好两个指针来分组:

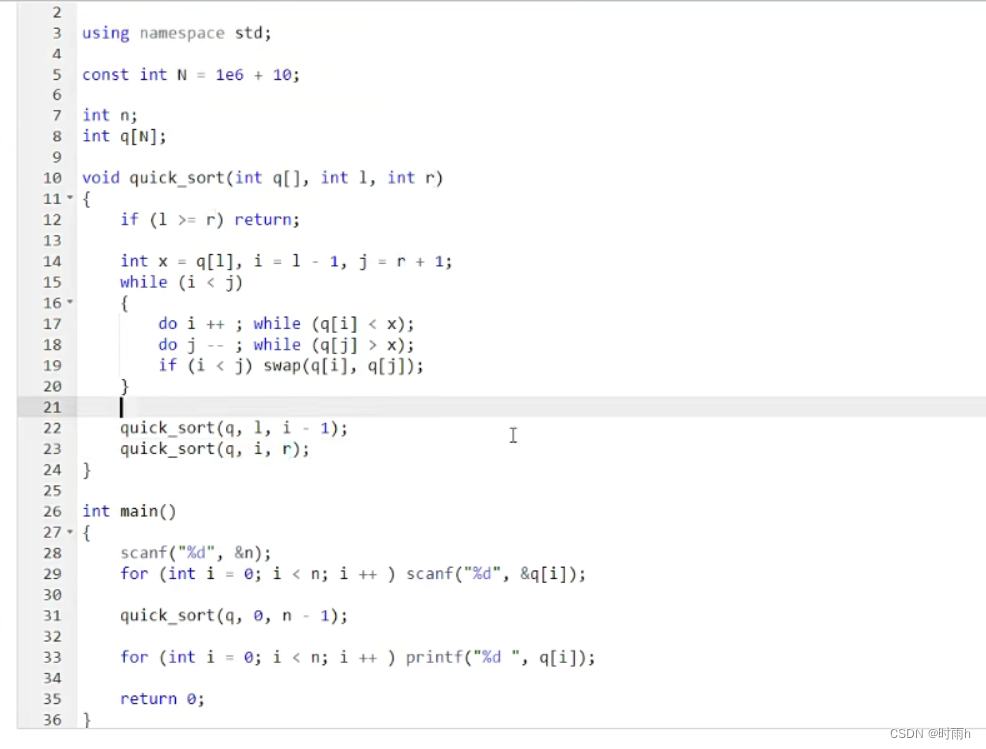
void quick_sort(int q[], int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];//先往中间进1才进行判断,要把数组整个包含进去,防止越界
while (i < j)
{
do i ++ ; while (q[i] < x);
do j -- ; while (q[j] > x);
if (i < j) swap(q[i], q[j]);//交换两个数
}
quick_sort(q, l, j), quick_sort(q, j + 1, r);
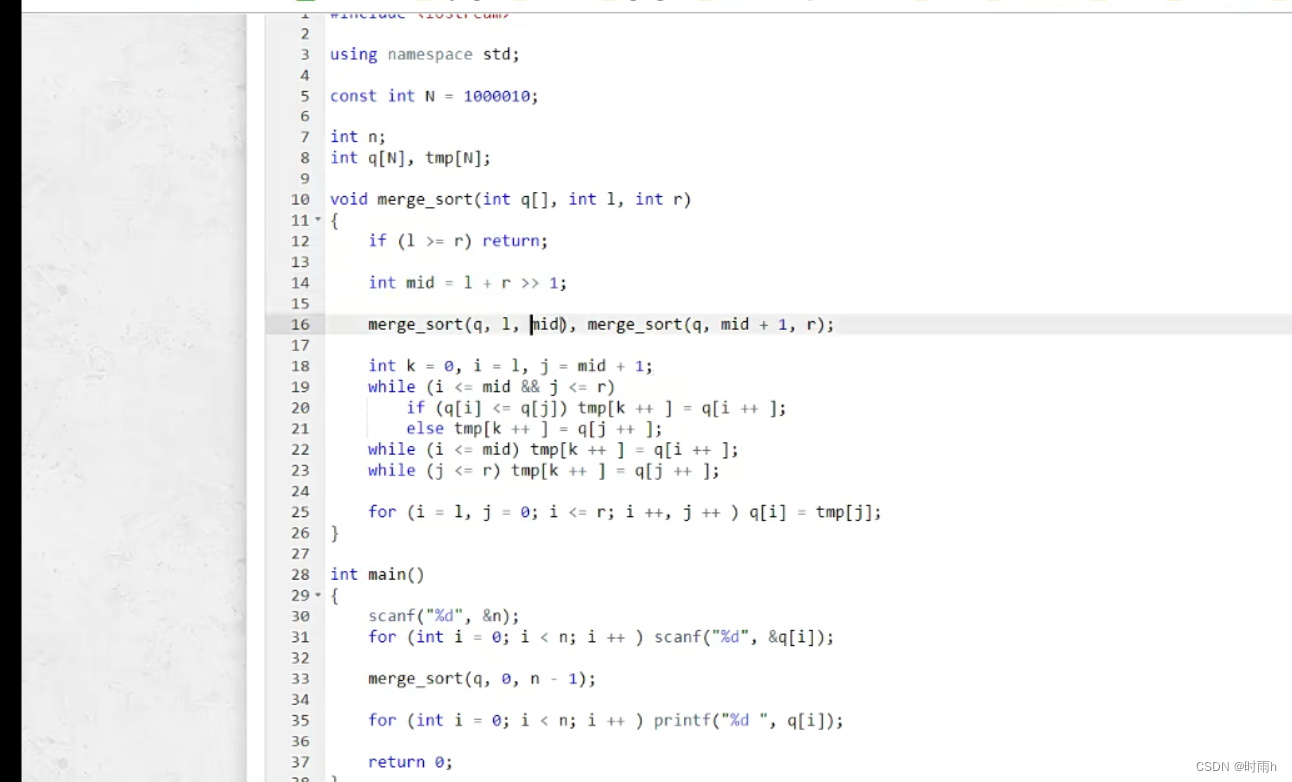
}归并排序算法模板 —— 模板题 AcWing 787. 归并排序
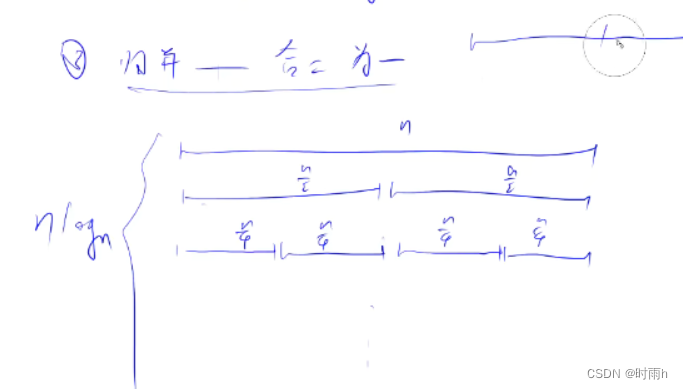
分治 先递归两边再去排3

时间复杂度:
void merge_sort(int q[], int l, int r)
{
if (l >= r) return;
int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] < q[j]) tmp[k ++ ] = q[i ++ ];
else tmp[k ++ ] = q[j ++ ];
while (i <= mid) tmp[k ++ ] = q[i ++ ];
while (j <= r) tmp[k ++ ] = q[j ++ ];
for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}
整数二分算法模板 —— 模板题 AcWing 789. 数的范围
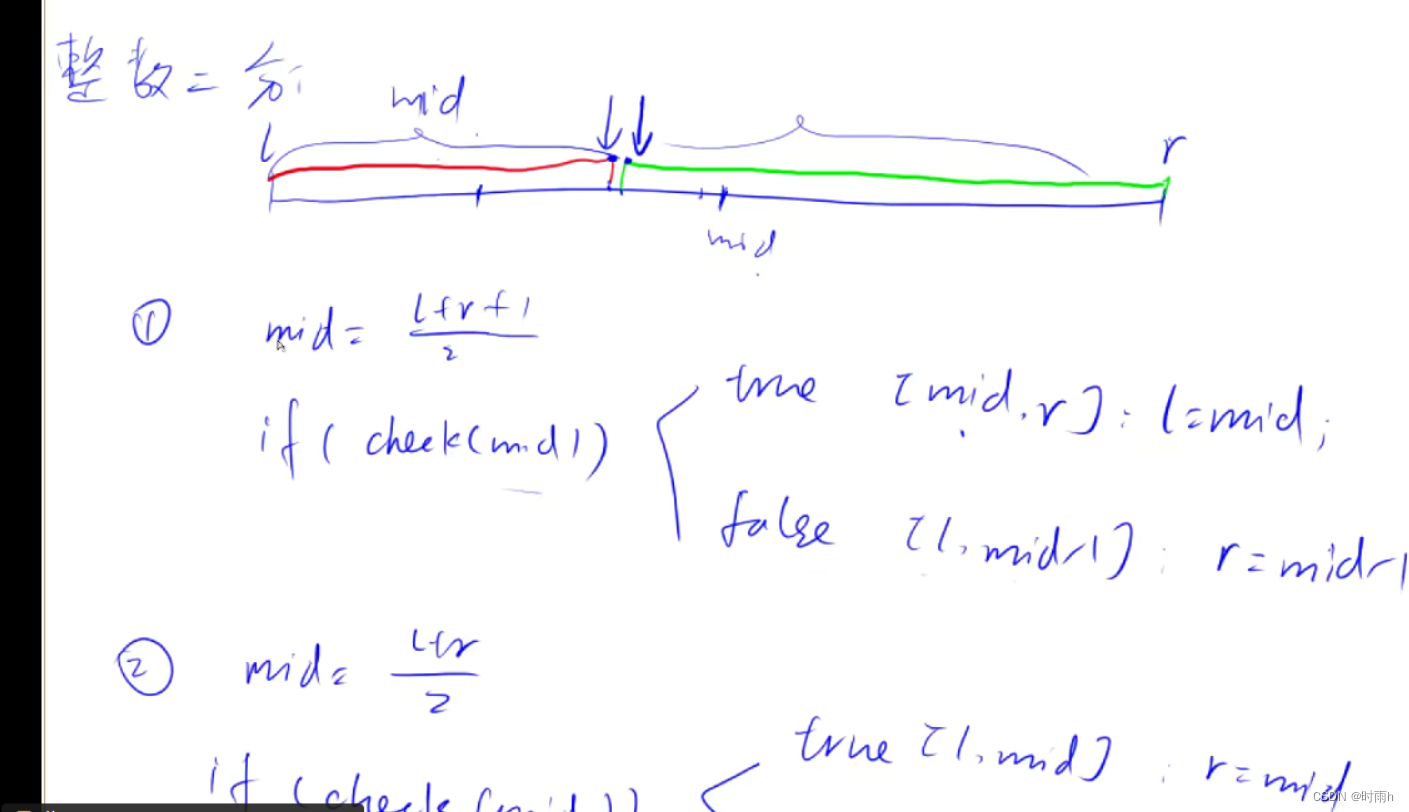
先用check去看mid等于什么去选择模版
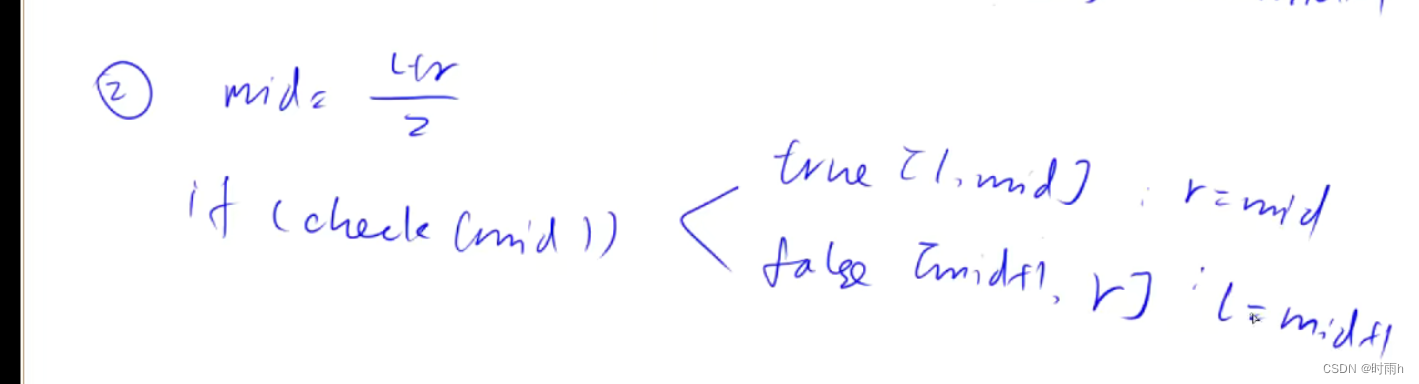
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
浮点数二分算法模板 —— 模板题 AcWing 790. 数的三次方根
bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{
const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求(比要求的多2一般不会有问题)
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}
高精度加法 —— 模板题 AcWing 791. 高精度加法

// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{
if (A.size() < B.size()) return add(B, A);
vector<int> C;
int t = 0;
for (int i = 0; i < A.size(); i ++ )
{
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if (t) C.push_back(t);
return C;
}
高精度减法 —— 模板题 AcWing 792. 高精度减法
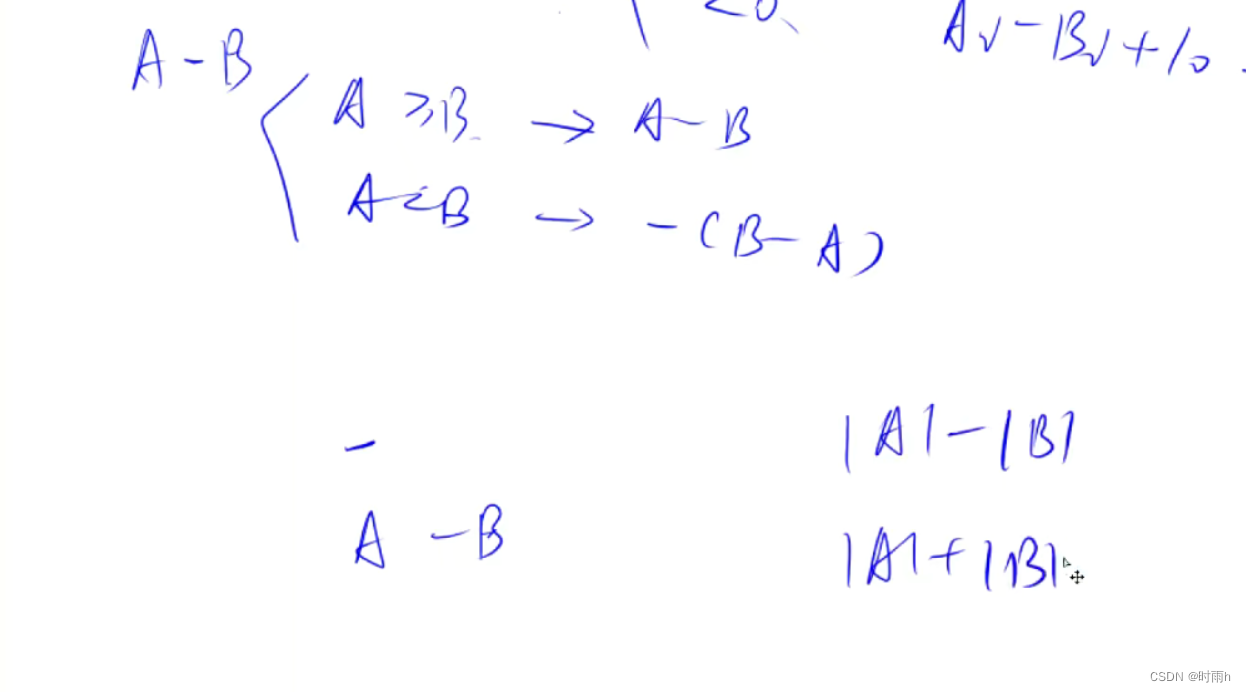
// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
vector<int> C;
for (int i = 0, t = 0; i < A.size(); i ++ )
{
t = A[i] - t;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if (t < 0) t = 1;
else t = 0;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
高精度乘低精度 —— 模板题 AcWing 793. 高精度乘法
// C = A * b, A >= 0, b > 0
vector<int> mul(vector<int> &A, int b)
{
vector<int> C;
int t = 0;
for (int i = 0; i < A.size() || t; i ++ )
{
if (i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
return C;
}
高精度除以低精度 —— 模板题 AcWing 794. 高精度除法
// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
vector<int> C;
r = 0;
for (int i = A.size() - 1; i >= 0; i -- )
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
一维前缀和 —— 模板题 AcWing 795. 前缀和
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]
二维前缀和 —— 模板题 AcWing 796. 子矩阵的和
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
一维差分 —— 模板题 AcWing 797. 差分
给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c
二维差分 —— 模板题 AcWing 798. 差分矩阵
给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c
位运算 —— 模板题 AcWing 801. 二进制中1的个数
求n的第k位数字: n >> k & 1
返回n的最后一位1:lowbit(n) = n & -n
双指针算法 —— 模板题 AcWIng 799. 最长连续不重复子序列, AcWing 800. 数组元素的目标和
for (int i = 0, j = 0; i < n; i ++ )
{
while (j < i && check(i, j)) j ++ ;
// 具体问题的逻辑
}
常见问题分类:
(1) 对于一个序列,用两个指针维护一段区间
(2) 对于两个序列,维护某种次序,比如归并排序中合并两个有序序列的操作
离散化 —— 模板题 AcWing 802. 区间和
vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素
// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1; // 映射到1, 2, ...n
}
区间合并 —— 模板题 AcWing 803. 区间合并
// 将所有存在交集的区间合并
void merge(vector<PII> &segs)
{
vector<PII> res;
sort(segs.begin(), segs.end());
int st = -2e9, ed = -2e9;
for (auto seg : segs)
if (ed < seg.first)
{
if (st != -2e9) res.push_back({st, ed});
st = seg.first, ed = seg.second;
}
else ed = max(ed, seg.second);
if (st != -2e9) res.push_back({st, ed});
segs = res;
}