异或相关算法

文章目录
- 1. 异或的性质
- 2. 题目一
- 3. 题目二
- 4. 题目三
- 5. 题目四
1. 异或的性质
我们知道,异或的定义是:相同为0,相异为1。所以也被称为无进位相加,根据这定义,我们可以得出三个性质:
1. N ^ N=0。2. N ^ 0=N。3. 异或满足结合律与交换率,所以一组数据,一起异或,结果一定是同一个值。
2. 题目一
如何不创建临时变量,交换两个值?
答案是:a=a ^ b,b=a ^ b,a=a ^ b。
证明:a=a ^ b,a变了,b没变。b=a ^ b,就等于b=a ^ b ^ b,b=a ^ 0,b=a。最后一步,a=a ^ b ^ a,就是a=b ^ 0,a=b。
两个数就进行交换了,但是这个方法只能用在a与b指向不同的内存空间,如果指向同一个内存空间,这样写会把此内存置成0。
3. 题目二
怎么把一个int类型的数,提取出最右侧的1来?
什么意思呢?

就是一个数a,如何得到ans这样的值,就是把最右侧的1提取出来。
答案是:a&(-a)或者a&((~a)+1)。这个大家可以自己证明一下。
4. 题目三
一个数组中有两种数出现了奇数次,其它数都出现了偶数次,怎么找到这两个数?
解题思路:假设出现两个奇数次的是a和b。
第一步:将数组里的数全部异或,那么结果就是a ^ b,因为其它都是偶数次,异或为0。
第二步:找出a ^ b最右侧的1位置,因为a和b是不同的,所以a ^ b一定不为0,所以a ^ b二进位中一定存在1的。
第三步:a ^ b二进位中的1位置,说明a和b在此位置上是不相等的。我们就把数组中所有此位置为1的分成一组,此位置为0的分成一组。
第四步:将此位置为1的异或在一起就能得出其中一个奇数次,在异或a ^ b,就能得出另外一个奇数次。
代码实现:

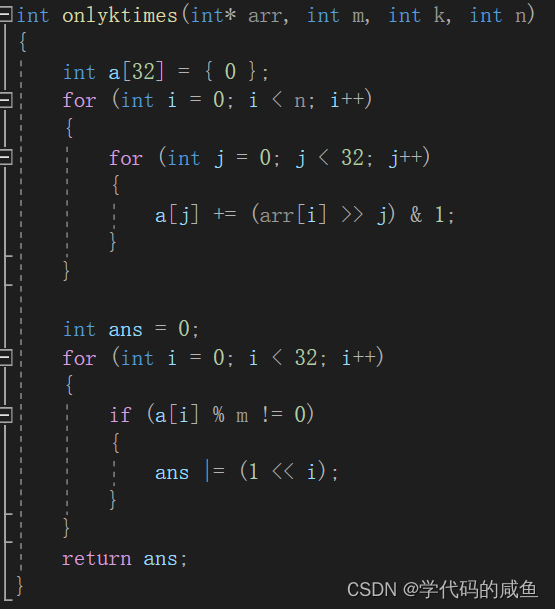
5. 题目四
一个数组中有一种数出现K次,其它数都出现了M次,M>1,K<M。找到出现K次的数。要求:时间复杂度O(N),空间复杂度O(1)。
解题思路:
第一步:因为一个int类型是32位,所以我们可以先定义一个32的数组。因为是常量数组所以空间复杂度是O(1)。。
第二步:遍历数组里所有数,如果这个数的某个位置是1,我们就在32位数组中这个位置上+1。

如果是4就在下标2的位置上+1,如果是12就在下标为2和3的位置上+1。
第三步:遍历这个32位数组,如果某位置上能被M整除,说明出现K次的那个数在此位置上为0,如果此位置不能被M整除,说明此位置上出现K次的那个数此位置为1。因为K<M,所有不存在能被M整除还存在出现K次的那个数。
假设K=3,M=7,某位置上1的个数是38,38不能被7整除,说明此位置上出现K此的那个数一定为1。
第四步:定义一个变量为0,如果此位置上不能整除,我们就左移1,然后或上去。
代码实现: