深入浅出梯度下降算法(学习笔记)
深入浅出梯度下降算法
正文
引言
在机器学习中,梯度下降算法(Gradient Descent)是一个重要的概念。它是一种优化算法,用于最小化目标函数,通常是损失函数。
简而言之,梯度下降帮助我们找到一个模型最优的参数,使得模型的预测更加准确。
本文将深入探讨梯度下降算法的原理、公式以及如何在Python中实现这一算法。
1. 梯度下降算法的理论基础
1.1 什么是梯度?
在数学中,梯度是一个向量,表示函数在某一点的变化率和方向。在多维空间中,梯度指向函数上升最快的方向。
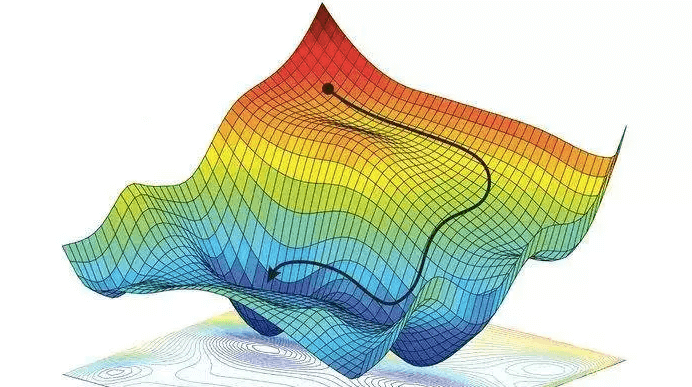
我们可以通过梯度来找到函数的最小值或最大值。对于损失函数,我们关注的是最小值。
1.2 梯度下降的基本思想
梯度下降的核心思想是通过不断调整参数,沿着损失函数的梯度方向移动,从而逐步逼近最小值。具体步骤如下:
1. 初始化参数:随机选择参数的初始值。
2. 计算梯度:计算损失函数对每个参数的梯度。
3. 更新参数:根据梯度信息调整参数,更新规则为:

其中:
是要优化的参数。
是学习率(step size),决定每次更新的幅度。
是损失函数关于参数的梯度。
4. 重复步骤:重复计算梯度和更新参数,直到收敛(即损失函数的变化非常小)。
2. 梯度下降的数学推导
假设我们有一个简单的线性回归问题,目标是最小化均方误差(MSE)损失函数:

其中是模型的预测值。为了使用梯度下降,我们需要计算损失函数关于参数的梯度:

通过求导,我们可以得到梯度表达式,并利用它来更新参数。
3. Python 实现梯度下降算法
接下来,我们将通过一个简单的线性回归示例来实现梯度下降算法。以下是实现代码:
3.1 导入库
import numpy as np
import matplotlib.pyplot as plt3.2 生成数据
我们将生成一些随机数据来模拟房屋面积与房价之间的线性关系。
# 生成数据
np.random.seed(0)
# 生成自变量X(房屋面积),范围在50到200平之间,共生成100个数据点
# 使用numpy的random.rand函数生成100个0到1之间的随机数
# 然后通过线性变换,将这些随机数的范围扩展到50到200
X = 50 + 150 * np.random.rand(100) # 生成从50到200的100个点
# 生成因变量 Y(房价),假设房价与房屋面积的关系
Y = 300000 + 2000 * X + np.random.randn(100) * 20000 # 线性关系加上噪声,价格范围在30万到50万之间
# 绘制生成的散点图
plt.scatter(X, Y, color='blue', alpha=0.5)
plt.title('房屋面积与房价的关系')
plt.xlabel('房屋面积 (平方米)')
plt.ylabel('房价 (人民币)')
plt.grid()
plt.show()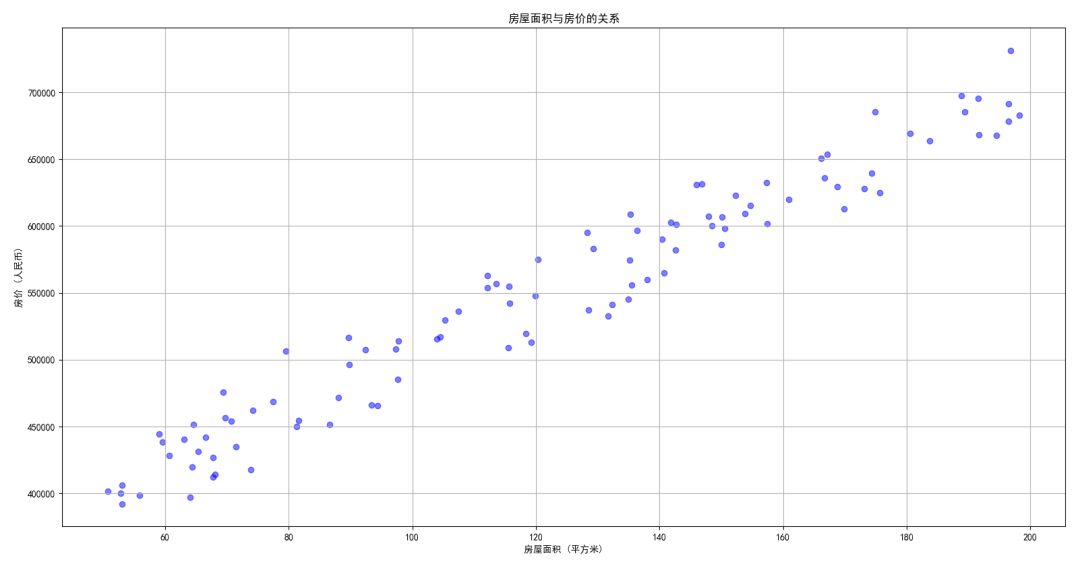
3.3 梯度下降实现
我们将实现梯度下降算法的核心部分。
# 将数据标准化,帮助梯度下降更快收敛
X = (X - np.mean(X)) / np.std(X)
Y = (Y - np.mean(Y)) / np.std(Y)
# 梯度下降参数
alpha = 0.01 # 学习率
num_iterations = 1000 # 迭代次数
m = len(Y) # 样本数量
# 初始化参数
theta_0 = 0 # 截距
theta_1 = 0 # 斜率
# 存储损失值
losses = []
# 梯度下降算法实现
for i in range(num_iterations):
# 计算预测值
Y_pred = theta_0 + theta_1 * X
# 计算损失函数 (MSE)
loss = (1/m) * np.sum((Y - Y_pred) ** 2)
losses.append(loss)
# 计算梯度
gradient_0 = -(2/m) * np.sum(Y - Y_pred) # 截距的梯度
gradient_1 = -(2/m) * np.sum((Y - Y_pred) * X) # 斜率的梯度
# 更新参数
theta_0 -= alpha * gradient_0
theta_1 -= alpha * gradient_1
print(f'截距 (θ0): {theta_0:.4f}, 斜率 (θ1): {theta_1:.4f}')截距 (θ0): 0.0000, 斜率 (θ1): 0.9743
3.4 绘制损失曲线
通过绘制损失函数随迭代次数变化的曲线,我们可以观察梯度下降的收敛过程。
# 绘制损失函数变化曲线
plt.figure()
plt.plot(range(num_iterations), losses, color='blue')
plt.title('损失函数随迭代次数的变化')
plt.xlabel('迭代次数')
plt.ylabel('损失值 (MSE)')
plt.grid()
plt.show()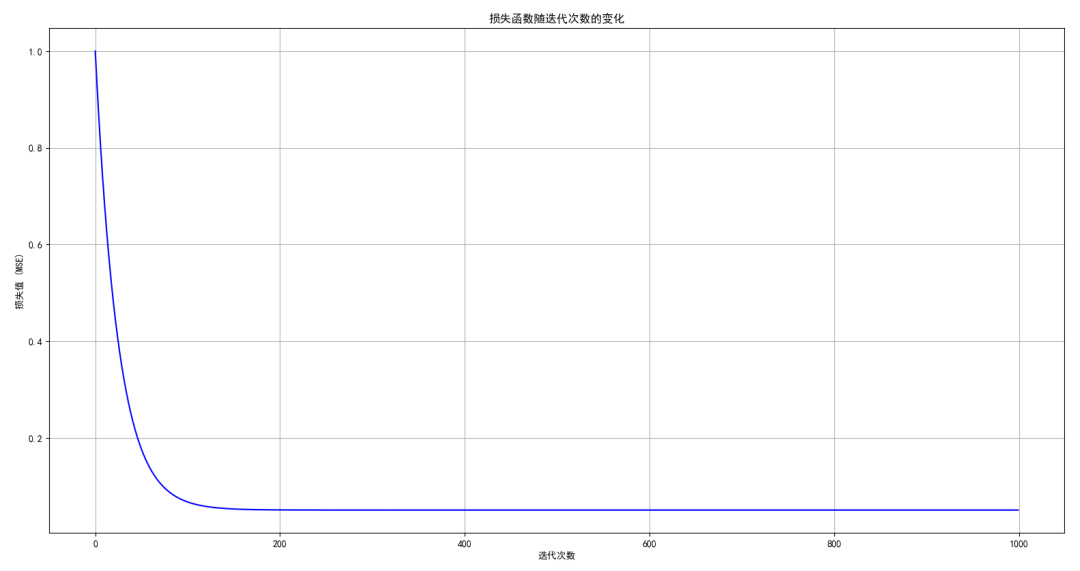
3.5 可视化回归线
最后,我们可以将训练好的回归线可视化,以观察模型的效果。
# 可视化回归线
plt.figure()
plt.scatter(X, Y, color='blue', alpha=0.5)
plt.plot(X, theta_0 + theta_1 * X, color='red', linewidth=2)
plt.title('梯度下降后的线性回归拟合')
plt.xlabel('房屋面积 (标准化)')
plt.ylabel('房价 (标准化)')
plt.grid()
plt.tight_layout() # 调整子图间距
plt.show()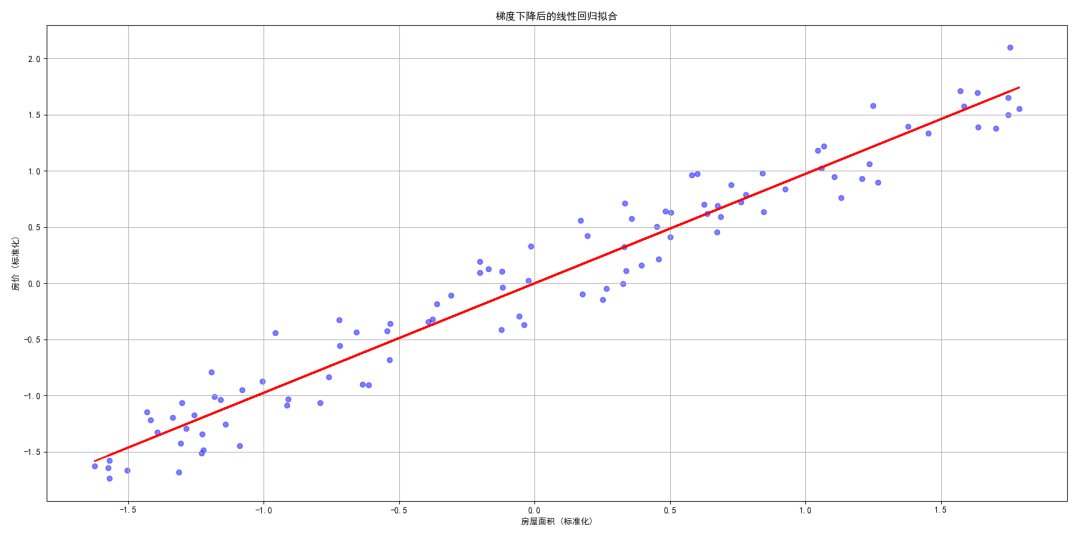
4. 梯度下降的应用场景
梯度下降算法在许多机器学习算法中得到了广泛应用,包括:
线性回归:如上文示例所示。
逻辑回归:用于分类问题,通过优化对数损失函数。
神经网络:用于深度学习,反向传播算法依赖于梯度下降来更新权重。
我们后面会一一讲到!
总结
梯度下降是一种强大的优化算法,它通过迭代更新参数来最小化损失函数。在实际应用中,选择合适的学习率和迭代次数至关重要,因为学习率过大可能导致发散,而学习率过小则可能导致收敛速度缓慢。
笔记部分
字体错误
在使用 Matplotlib 绘制包含中文字符的图表时,可能会遇到 Glyph ... missing from current font 的警告。这是因为默认字体不支持中文字符。可以通过以下方式解决这个问题:
1. 设置支持中文的字体
在代码中手动设置 Matplotlib 使用支持中文的字体(如 SimHei 字体):
import matplotlib.pyplot as plt
from matplotlib import font_manager
# 设置字体为 SimHei
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False # 解决坐标轴负号显示问题
2. 直接指定字体路径
也可以通过 FontProperties 来指定具体的字体文件路径:
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
# 指定字体文件路径
font_path = "C:/Windows/Fonts/simhei.ttf" # 你可以根据系统实际路径调整
font_prop = FontProperties(fname=font_path)
plt.title("标题示例", fontproperties=font_prop)
plt.show()
3. 安装支持中文的字体(适用于缺少中文字体的环境)
在某些环境中(如 Ubuntu),需要先安装中文字体:
sudo apt-get install fonts-wqy-zenhei
然后在代码中使用这类字体即可。
梯度向量
图中的公式是关于梯度向量的表示,它描述了在参数空间中目标函数的变化情况。让我们逐步解释其中的每个部分。
公式解释
公式中的符号和含义如下:

- ∇J(θ):梯度符号 ∇ 表示函数 J 的梯度,θ 是函数 J 的参数向量(例如,θ = [θ0,θ1])。
- J(θ):目标函数,通常是损失函数或成本函数,例如在机器学习中的均方误差损失函数。这个函数随着参数 θ 的变化而变化。
- ∂J/∂θ0 和 ∂J/∂θ1:分别是对参数 θ0 和 θ1 的偏导数。这些偏导数描述了 J(θ) 在 θ0 和 θ1 方向上的变化率。偏导数的值表示在某个方向上增加或减少参数时,目标函数的增大或减小程度。
梯度向量的意义
梯度 ∇J(θ)是一个向量,它指向目标函数 J(θ)上升最快的方向。在机器学习的梯度下降算法中,更新参数时会朝着梯度的相反方向(即函数下降最快的方向)移动,以最小化 J(θ)。
梯度下降更新公式
假设我们要最小化目标函数 J(θ),梯度下降的更新公式为:
θ = θ − α⋅∇J(θ)
其中:
- α 是学习率,控制更新步伐的大小。
- θ 是当前参数值,通过减去梯度的方向,使 J(θ) 趋于最小。
总结
此公式用于计算目标函数 J 关于参数向量 θ 的梯度。通过梯度信息,优化算法可以找到目标函数的最小值(或最大值),并且梯度的每个分量(即每个偏导数)告诉我们如何调整各个参数以达到目标函数的优化。
图中的公式是关于梯度向量的表示,它描述了在参数空间中目标函数的变化情况。让我们逐步解释其中的每个部分。
标准差
标准差(Standard Deviation)是统计学中用于衡量数据集的离散程度的指标。它表示数据点与平均值之间的平均偏离程度。标准差越小,数据越集中;标准差越大,数据的分散程度越大。
计算标准差的公式
假设有一组数据 X={x1,x2,…,xn},其均值为 μ。标准差的计算分为样本标准差和总体标准差:
-
总体标准差(当我们有整个数据集时):

其中:- σ:总体标准差
- n:数据总数
- xi:第 i 个数据点
- μ:数据的平均值,即

-
样本标准差(当我们有一个样本数据集时):

其中:
- s:样本标准差
- n:样本数据的数量
- xi:第 i 个数据点
- xˉ:样本的平均值,即

标准差的意义
- 低标准差:数据点接近平均值,数据比较集中。
- 高标准差:数据点分布较广,与平均值偏离较大,数据分散。
示例
假设有一组数据 {2,4,4,4,5,5,7,9},我们可以计算其平均值,然后计算各个数据点与平均值的偏离,最终得到标准差。
标准差的应用
标准差广泛应用于数据分析、工程、金融和科学研究中,用于分析数据的波动情况,评估风险等。例如:
- 在股票市场中,较高的标准差可能意味着较高的价格波动。
- 在质量控制中,小的标准差表示产品的质量更加稳定。
标准差是一个重要的统计量,帮助我们了解数据集的波动情况和离散程度。
标准化(归一化)数据

在数据处理中用于标准化(归一化)数据,将数据调整为零均值和单位标准差。这个过程称为标准分数(Z-score)标准化,其意义如下:
公式解析
- np.mean(X):计算数据集 X 的平均值。
- np.std(X):计算数据集 X 的标准差。
- X−np.mean(X):每个数据点减去均值,使数据中心移动到 0。
- X−np.mean(X)/np.std(X):每个数据点与均值的偏差除以标准差,这一步将数据的分布缩放为单位标准差(1)。
标准化的结果
- 均值为 0:标准化后,数据的均值会变成 0。
- 标准差为 1:标准化后的数据标准差为 1,数据点在正态分布情况下会大部分集中在 [-1, 1] 之间。
标准化的意义
-
特征均衡:在机器学习中,不同特征的尺度不同(如收入单位是美元、身高单位是厘米),标准化可以让不同特征的数值范围相近,以避免某个特征对模型的影响过大。
-
加快收敛:在梯度下降等优化算法中,标准化可以使算法更快地收敛。
-
对称性:在数据分析和可视化中,标准化可以帮助我们更容易比较不同数据集之间的变化。
示例
假设 X=[1,2,3,4,5],则标准化后的 XXX 会是一个均值为 0、标准差为 1 的数据集,使得数据可以更适合大多数机器学习模型的输入。

在上面的图中:
-
左图显示了原始数据 [1,2,3,4,5]。
-
右图显示了标准化后的数据。这些值经过 Z-score 标准化处理,均值为 0,标准差为 1。可以看到,数据被缩放到一个中心在 0、范围大致在 -2 到 2 之间的区间。
标准化有助于在特征值差异较大时,让数据更加均匀,便于机器学习模型处理。
import numpy as np
import matplotlib.pyplot as plt
# 原始数据
X = np.array([1, 2, 3, 4, 5])
X_mean = np.mean(X)
X_std = np.std(X)
# 标准化数据
X_standardized = (X - X_mean) / X_std
# 画图
plt.figure(figsize=(10, 5))
# 原始数据图
plt.subplot(1, 2, 1)
plt.stem(X, use_line_collection=True)
plt.title("Original Data")
plt.xlabel("Index")
plt.ylabel("Value")
plt.ylim(0, 6)
# 标准化数据图
plt.subplot(1, 2, 2)
plt.stem(X_standardized, use_line_collection=True)
plt.title("Standardized Data")
plt.xlabel("Index")
plt.ylabel("Value (Standardized)")
plt.ylim(-2, 2)
plt.tight_layout()
plt.show()梯度下降算法
参数设定
alpha = 0.01 # 学习率
num_iterations = 1000 # 迭代次数
m = len(Y) # 样本数量
-
alpha:学习率,用于控制每次参数更新的幅度。较高的学习率可能使得收敛更快,但过高可能导致模型不收敛。
-
num_iterations:算法迭代的次数,即更新参数的次数。更多的迭代次数可以帮助模型更好地拟合数据。
-
m:样本数量,用于计算平均损失和梯度。
初始化参数
theta_0 = 0 # 截距
theta_1 = 0 # 斜率
-
theta_0 和 theta_1:模型参数。初始值都设为 0,其中
theta_0是截距,theta_1是特征X的系数(斜率)。
存储损失值
losses = []
-
losses:用于记录每次迭代的损失值(误差)。通过存储损失值可以观察模型的收敛情况。
梯度下降算法实现
for i in range(num_iterations):
-
使用一个循环,执行
num_iterations次梯度下降步骤。
1. 计算预测值
Y_pred = theta_0 + theta_1 * X
-
Y_pred:根据当前的参数
theta_0和theta_1计算预测值。对于每个样本 xi,预测值为 yi = θ0 + θ1 · xi 。
2. 计算损失函数
loss = (1/m) * np.sum((Y - Y_pred) ** 2)
losses.append(loss)
-
loss:计算损失函数(均方误差,MSE),衡量预测值
Y_pred和实际值Y的差距。公式为:
-
losses.append(loss):将损失值添加到列表
losses中,以便观察损失值随迭代次数的变化。
3. 计算梯度
gradient_0 = -(2/m) * np.sum(Y - Y_pred) # 截距的梯度
gradient_1 = -(2/m) * np.sum((Y - Y_pred) * X) # 斜率的梯度
-
gradient_0:截距
theta_0的梯度。它表示损失函数对theta_0的变化率,用来调整theta_0的值。公式为:
-
gradient_1:斜率
theta_1的梯度。它表示损失函数对theta_1的变化率,用来调整theta_1的值。公式为:
4. 更新参数
theta_0 -= alpha * gradient_0
theta_1 -= alpha * gradient_1
-
theta_0 -= alpha * gradient_0:使用学习率
alpha和梯度gradient_0更新theta_0。梯度指明了损失函数下降的方向,乘以alpha控制更新步长。 -
theta_1 -= alpha * gradient_1:使用学习率
alpha和梯度gradient_1更新theta_1。
通过每次迭代更新 theta_0 和 theta_1,梯度下降算法会逐渐找到使损失最小的参数。
rand和randn的说明
在 NumPy 中,rand 和 randn 都是用于生成随机数的函数,但它们生成的随机数分布不同:
1. np.random.rand()
- 分布:生成的随机数符合均匀分布,即在指定范围内(通常是 [0,1))的每个数值出现的概率相同。
- 范围:生成的值在 [0,1) 区间内。
- 用法:
np.random.rand(d0, d1, ..., dn),参数可以是多个维度,指定生成数组的形状。 - 示例:
np.random.rand(3, 2) # 生成一个 3x2 的矩阵,元素均在 [0, 1) 内
2. np.random.randn()
- 分布:生成的随机数符合标准正态分布(均值为 0,标准差为 1)。
- 范围:理论上没有固定的范围,但数据大部分集中在 [−3,3] 之间。
- 用法:
np.random.randn(d0, d1, ..., dn),参数也可以指定生成数组的形状。 - 示例:
np.random.randn(3, 2) # 生成一个 3x2 的矩阵,元素符合标准正态分布
总结
rand生成的是 [0,1) 区间的均匀分布随机数。randn生成的是均值为 0、标准差为 1 的标准正态分布随机数。
