快速上手机器学习-朴素贝叶斯
朴素贝叶斯
引言:本文通过介绍先验概率,后验概率,条件概率计算和贝叶斯定理等概率论内容引入朴素贝叶斯分类算法的基本思路,朴素贝叶斯的最终分类思想是将输入分类给概率最大的类,这也是概率模型算法的共有思想。本文专注于先验概率后验概率以及最终贝叶斯分类器的公式推导,旨在帮助读者深入浅出的理解算法模型,读者可以将本文视为《统计学习方法》第三章朴素贝叶斯算法的理解和导读。
关键字:极大似然估计,贝叶斯定理,后验概率最大化
参考文献:统计学习方法 (第2版)-李航,刘建平老师的博客
朴素贝叶斯模型,对于很多刚上手机器学习的同学来说(尤其是我)是当头一棒毫不夸张,原因主要是两点:(1)太抽象 (2)没有头绪不知道从哪开始进行。难以建立学习起点,难以搭建学习框架。在看统计学习方法这本书时更是一头雾水,满篇的公式推导,它认识我我不认识它。尤其是一堆的条件概率公式,哪怕我知道了什么是条件概率,在学习过程中依然不知道怎么去做。
我们反复强调机器学习中数学基础的重要性,朴素贝叶斯模型理论根本就建立于概率论,甚至几乎没有什么高数需要的概念,有兴趣的同学可以在文章外系统的学习一下《概率论与数理统计》同济大学出版社一,二,七章。重点学习理解事件分析,概率计算,条件概率,全概率公式,贝叶斯定理,参数估计中的点估计部分。
1. 所属分类和相关概念
1.1 先验概率和后验概率
处于现实社会中的我们远远要比机器有经验的多,就像是我们知道当你家蠢猫在你的书桌上开始拨弄水杯的时候,这个水杯摔碎的概率至少有80%。如果我们在一个地方长期生活了很久,在夏天出门时看到乌云密布,我们往往会带上雨伞,因为这个地方同一时期同一种天气情况,下雨的概率往往达到了90%,一不小心你就会痛苦的在雨中狂奔。
这种感觉很模糊,并不像饿了需要进食一样存在在基因当中,你甚至可以用意志违背这种感觉,享受雨中的湿润空气,但是你的经验也告诉你,多半你的衣服需要重新洗,而你也因此可能感冒,发烧,甚至危及你的生命。
显然,规避风险,预测事件发生,这是人类后天为了维护机体健康而学习到的经验。而这种由历史数据+主观判断得出对某一件事情发生概率的估计,就是先验概率。
但是作为人类中特殊的一群人,以前叫巫,后来入职钦天监有了公职,再后来借助工具保证人民可以提前收晒秋的麦子而不被老妈揍,担任如此的重职,你显然不能只根据经验和感官去判断,因为经验告诉你不要过分相信经验。所以你不仅需要参照已有的先验概率,同时也需要参考最近一段时间天气卫星记录的数据,比如降雨量,湿度,甚至是有没有一股从xx洋或者x伯利亚刮来的暖风或者寒流。
而参照先验概率+新数据所预估出的事件发生的概率就叫做:后验概率。先验概率和后验概率的核心区别在于,有没有考虑新数据。
1.2 条件概率,全概率公式和贝叶斯定理
1.2.1 条件概率
我们一般会用 P ( A / B ) P(A/B) P(A/B)来表示条件概率,它可以简单的表达:在B发生的情况下A发生的概率这一含义,嗯,说了和没说一样,那我们不妨举个栗子来解释一下:
如果我们现在有十个完全相同的水杯,里面装满了十杯完全看不出区别的水/白酒,其中只有三杯是白水,现在你和你的室友一起喝酒,那么你喝到白酒的概率是多少呢: 3 10 \frac{3}{10} 103,如果你的舍友比你先喝,他说他喝到的是白酒,嗯,姑且相信他。那么在你室友喝了一杯白酒之后,你喝到白酒的概率就变成了: 2 9 \frac{2}{9} 92。
这就是在你室友喝了白酒之后你喝到白酒这件事的概率。要计算条件概率重点是考虑状态的转换,之前的状态是谁都没喝,这是事实,而经过你的舍友喝了一杯这个事实后,状态转为了现在只有九杯且只剩下两杯。还是不好理解,不妨我们现在通过一个公式来加深理解:
P
(
A
/
B
)
=
P
(
A
B
)
P
(
B
)
P(A/B) = \frac{P(AB)}{P(B)}
P(A/B)=P(B)P(AB)
这个公式分子代表AB同时发生的概率,而分母代表B发生的概率。
1.2.2 全概率公式
如果我们的现在有一块蛋糕,长5M,宽3M,被平均分成了五块,而蛋糕的中央有一块草莓集中的区域长4M,宽1M,我们都喜欢吃草莓,我和我的四个舍友一起当大胃王吃蛋糕,那么我们吃到草莓的概率各自是多少呢?显然我们各自迟到蛋糕的概率是 1 5 \frac{1}{5} 51
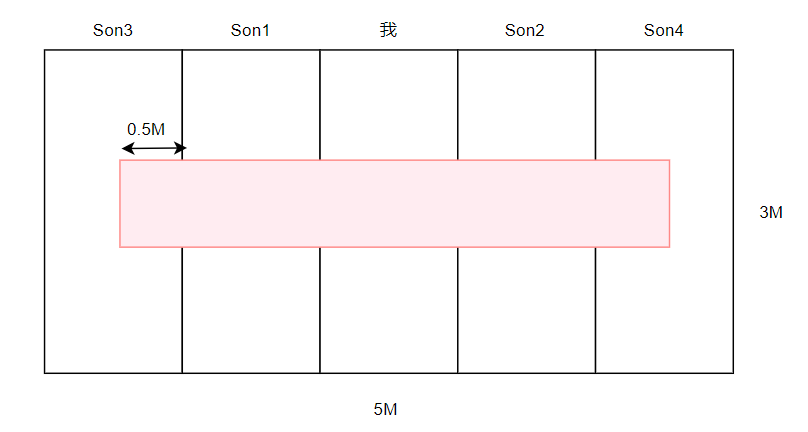
同时我们可以通过简单的计算得到各自吃到草莓的概率:
P
(
M
e
)
=
P
(
吃到草莓
/
吃到蛋糕
)
=
1
∗
1
1
∗
3
=
1
3
P
(
S
o
n
1
)
=
P
(
吃到草莓
/
吃到蛋糕
)
=
1
∗
1
1
∗
3
=
1
3
P
(
S
o
n
2
)
=
P
(
吃到草莓
/
吃到蛋糕
)
=
1
∗
1
1
∗
3
=
1
3
P
(
S
o
n
3
)
=
P
(
吃到草莓
/
吃到蛋糕
)
=
0.5
∗
1
1
∗
3
=
=
1
6
P
(
S
o
n
4
)
=
P
(
吃到草莓
/
吃到蛋糕
)
=
0.5
∗
1
1
∗
3
=
=
1
6
P(Me)=P(吃到草莓/吃到蛋糕)=\frac{1*1}{1*3}=\frac{1}{3}\\ P(Son1)=P(吃到草莓/吃到蛋糕)=\frac{1*1}{1*3}=\frac{1}{3}\\ P(Son2)=P(吃到草莓/吃到蛋糕)=\frac{1*1}{1*3}=\frac{1}{3}\\ P(Son3)=P(吃到草莓/吃到蛋糕)=\frac{0.5*1}{1*3}==\frac{1}{6}\\ P(Son4)=P(吃到草莓/吃到蛋糕)=\frac{0.5*1}{1*3}==\frac{1}{6}\\
P(Me)=P(吃到草莓/吃到蛋糕)=1∗31∗1=31P(Son1)=P(吃到草莓/吃到蛋糕)=1∗31∗1=31P(Son2)=P(吃到草莓/吃到蛋糕)=1∗31∗1=31P(Son3)=P(吃到草莓/吃到蛋糕)=1∗30.5∗1==61P(Son4)=P(吃到草莓/吃到蛋糕)=1∗30.5∗1==61
那我们整体吃到草莓的概率是多少呢:
P
(
S
t
r
a
w
b
e
r
r
y
)
=
1
∗
4
3
∗
5
=
4
15
P(Strawberry) = \frac{1*4}{3*5} =\frac{4}{15}
P(Strawberry)=3∗51∗4=154
这个数值恰好等于:
P
(
S
t
r
a
w
b
e
r
r
y
)
=
3
∗
[
P
(
M
E
)
∗
1
5
+
P
(
S
o
n
1
)
∗
1
5
+
P
(
S
o
n
2
)
∗
1
5
+
P
(
S
o
n
3
)
∗
1
5
+
P
(
S
o
n
4
)
∗
1
5
]
P(Strawberry) = 3 *[ P(ME)*\frac{1}{5}+P(Son1)*\frac{1}{5}+P(Son2)*\frac{1}{5}+P(Son3)*\frac{1}{5}+P(Son4)*\frac{1}{5}]
P(Strawberry)=3∗[P(ME)∗51+P(Son1)∗51+P(Son2)∗51+P(Son3)∗51+P(Son4)∗51]
是什么意思呢,如果我们设吃到蛋糕这个事件为B,吃到草莓这个事件为A,那么我们全体吃到蛋糕的概率就是:也就是我们ABi同时发生的概率
P
(
A
)
=
∑
i
n
P
(
A
B
i
)
P(A) = \sum_i^{n}P(AB_i)
P(A)=i∑nP(ABi)
如果用条件概率来表示就是:
P
(
A
)
=
∑
i
n
P
(
B
=
B
i
)
⋅
P
(
A
/
B
=
B
i
)
P(A) = \sum_i^{n} P(B=B_i)\cdot P(A/B=B_i)
P(A)=i∑nP(B=Bi)⋅P(A/B=Bi)
1.2.3 贝叶斯定理
首先我们还是从蛋糕问题出发,如果今天是我生日,我先吃第一口,我们知道吃到草莓的概率是P(A),那么是我吃到草莓的概率怎么表示呢?即: P ( B m e / A ) P(B_{me}/A) P(Bme/A)
那么这个式子就可以表示为: P ( B m e / A ) = P ( A B m e ) P ( A ) P(B_{me}/A) = \frac{P(AB_{me})}{P(A)} P(Bme/A)=P(A)P(ABme)
如果用条件概率表示:$P(B_{me}/A) = \frac{P(B=B_{me})\cdot P(A/B=B_{me})}{\sum_i^{n} P(B=B_i)\cdot P(A/B=B_i)} $
这就是贝叶斯公式:形式上可以理解为条件和事件位置交换后的概率,即将原来的条件变为事件,将原来的事件变为条件,从几何角度可以这样理解:求图中绿色部分的概率
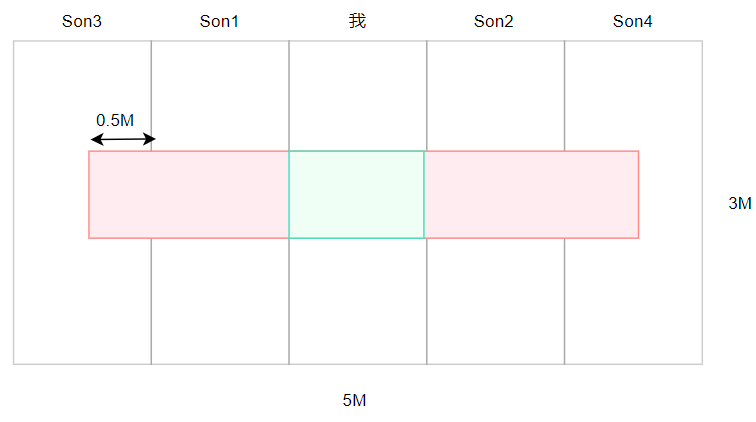
1.3 条件独立
两个事情如果之间没有相关性就称为条件独立,比如说你和你室友同样喝酒,如果你室友只是拿起来喝了一杯,啥也没说,然后你另一个室友立刻用原来的水/白酒补满杯子,那么这个时候你舍友和你喝到白酒的概率都是 3 10 \frac{3}{10} 103。因为你舍友喝了酒之后并没有影响到你会不会喝到白酒这件事,这就叫条件独立。
而条件独立的两个事件满足:
P
(
A
B
)
=
P
(
A
)
P
(
B
)
P(AB)=P(A)P(B)
P(AB)=P(A)P(B)
你和你舍友一起喝到白酒的概率是:
9
100
\frac{9}{100}
1009
而在我们 1.2的例子中,
P
(
B
)
=
3
10
,
P
(
A
/
B
)
=
2
9
P(B)=\frac{3}{10},P(A/B)=\frac{2}{9}
P(B)=103,P(A/B)=92,则你们一起喝到白酒的概率是:
6
90
\frac{6}{90}
906,显然你舍友先喝到白酒影响到了你喝到白酒的概率,而你们俩喝白酒这件事是不独立。
以上我们所有解释的概率公式如下:
I
F
A
B
独立
,
则
P
(
A
B
)
=
P
(
A
)
P
(
B
)
P
(
A
/
B
)
=
P
(
A
B
)
P
(
B
)
;
P
(
B
/
A
)
=
P
(
A
B
)
P
(
A
)
P
(
A
/
B
)
=
P
(
B
/
A
)
P
(
A
)
P
(
B
)
全概率公式:如果
B
1
,
B
2
.
.
B
n
可以将一个概率空间
1
全部划分
,
∀
B
i
,
B
j
,
i
!
=
j
B
i
∩
B
j
=
∅
P
(
a
)
=
∑
i
=
1
n
P
(
B
i
)
P
(
A
/
B
i
)
贝叶斯定理:
P
(
B
i
/
A
)
=
P
(
B
i
)
P
(
A
/
B
i
)
∑
j
=
1
n
P
(
B
j
)
P
(
A
/
B
j
)
IF \quad AB独立,则P(AB)=P(A)P(B)\\ P(A/B) = \frac{P(AB)}{P(B)};P(B/A) = \frac{P(AB)}{P(A)}\\ P(A/B) = \frac{P(B/A)P(A)}{P(B)}\\ 全概率公式:如果B_1,B_2..B_n可以将一个概率空间1全部划分,\forall B_i,B_j,i!=j\\ B_i \cap B_j = \varnothing\\ P(a) = \sum_{i=1}^{n}P(B_i)P(A/B_i)\\ 贝叶斯定理: P(B_i/A) = \frac{P(B_i)P(A/B_i)} {\sum_{j=1}^{n}P(B_j)P(A/B_j)}
IFAB独立,则P(AB)=P(A)P(B)P(A/B)=P(B)P(AB);P(B/A)=P(A)P(AB)P(A/B)=P(B)P(B/A)P(A)全概率公式:如果B1,B2..Bn可以将一个概率空间1全部划分,∀Bi,Bj,i!=jBi∩Bj=∅P(a)=i=1∑nP(Bi)P(A/Bi)贝叶斯定理:P(Bi/A)=∑j=1nP(Bj)P(A/Bj)P(Bi)P(A/Bi)
1.4 0-1分布,伯努利分布
如果一个事件只有发生和不发生两种结果,假设发生的概率是P,那么不发生的概率就为1-P,如果我们现在做N次独立实验,假设这个实验中事件发生了K次,那么事件发生K次这个事件发生的概率是多少呢?
P
(
X
=
k
)
=
C
n
k
p
k
(
1
−
p
)
n
−
k
P(X=k) = C_{n}^{k}p^{k}(1-p)^{n-k}
P(X=k)=Cnkpk(1−p)n−k
符合这种事件发生形式的事件,我们称这个事件服从伯努利分布:
X
∼
B
(
n
,
p
)
X\sim B(n,p)
X∼B(n,p)
如果我们只进行一次实验,那么这个时候事件就转为了1重伯努利分布,即: X ∼ B ( 1 , p ) X\sim B(1,p) X∼B(1,p),也就是我们常说的0-1分布,
如果我们现在有两个随机变量X,Y,这两个随机变量一个 X ∼ B ( n 1 , p ) X\sim B(n_1,p) X∼B(n1,p),另一个 Y ∼ B ( n 2 , p ) Y\sim B(n_2,p) Y∼B(n2,p),那么随机变量X+Y这个组合随机变量则服从 X + Y = B ( n 1 + n 2 , p ) X+Y = B(n_1+n_2,p) X+Y=B(n1+n2,p)
对于事件加法,我们这可以这样理解,例如:假设有两个独立的抛硬币实验,用随机变量X表示抛第一个硬币正面朝上为1,反面朝上为0;随机变量Y表示抛第二个硬币正面朝上为1,反面朝上为0。如果我们定义随机变量 Z = X + Y Z=X+Y Z=X+Y,Z这个离散型随机变量就可以表示抛两个硬币朝上次数这个事件。
如果我们现在先对硬币一号抛3次,则硬币一号3次实验中有几次朝上这个事件服从 X ∼ B ( 3 , p ) X\sim B(3,p) X∼B(3,p),同理再对硬币二号也抛4次,则硬币二号4次实验中有几次朝上这个事件服从 Y ∼ B ( 4 , p ) Y\sim B(4,p) Y∼B(4,p),则抛硬币一号与二号有几次朝上这个事件就服从:$X+Y \sim B(7,p) ,从意义上就可以理解为同一个硬币抛七次中正面朝上的概率分布。甚至我们可以理解为第一个是抛硬币 3 次,第二个是抛猫 4 次,猫四脚朝上的概率也是 p ,则抛硬币和抛猫这个两个事件朝上次数也服从 ,从意义上就可以理解为同一个硬币抛七次中正面朝上的概率分布。甚至我们可以理解为第一个是抛硬币3次,第二个是抛猫4次,猫四脚朝上的概率也是p,则抛硬币和抛猫这个两个事件朝上次数也服从 ,从意义上就可以理解为同一个硬币抛七次中正面朝上的概率分布。甚至我们可以理解为第一个是抛硬币3次,第二个是抛猫4次,猫四脚朝上的概率也是p,则抛硬币和抛猫这个两个事件朝上次数也服从X+Y \sim B(7,p) $
???感兴趣的同学可以重点学习一下事件分析。
1.5 多项式分布
对于伯努利分布来说,事件的结果只有发生和不发生两种,那么如果现在事件有更多的情况,比如说抛骰子,事件就有6种情况,我们假设现在在抛灌了水银的假骰子,各个面的概率为:
| 事件 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| P | 0.1 | 0.2 | 0.3 | 0.2 | 0.1 | 0.1 |
则若抛十次,即n=10,其中出现:
| n1 | n2 | n3 | n4 | n5 | n6 |
|---|---|---|---|---|---|
| 2 | 3 | 1 | 2 | 1 | 1 |
事件的概率的概率为多少?类似服从这样的概率模型,我们就称这个事件为多项式分布,而案例中事件的概率是:
P
(
n
1
,
n
2
.
.
.
n
6
)
=
n
!
n
1
!
⋅
n
2
!
.
.
.
⋅
n
6
!
∗
P
1
n
1
⋅
P
2
n
2
.
.
.
P
6
n
6
⋅
P(n_1,n_2...n_6)=\frac{n!}{n_1!\cdot n_2!...\cdot n_6!}*P_1^{n_1}\cdot P_2^{n_2}...P_6^{n_6}\cdot
P(n1,n2...n6)=n1!⋅n2!...⋅n6!n!∗P1n1⋅P2n2...P6n6⋅
1.6 点估计-极大似然估计
如果说我们现在有一组样本,这组样本服从什么样的概率分布我们知道,但是这个分布是含有参数的【有一个参数位置,比如说X~B(n,p)而p未知】,显然这组样本也可以理解为是根据概率分布而产生的数据,那么我们就可以通过这组样本来估计分布函数的参数。
给定一个独立同分布的样本 x 1 , x 2 , . . . x n x_1,x_2,...x_n x1,x2,...xn样本服从参数为 θ \theta θ的概率分布,那么样本同时发生的概率就可以理解为: P ( X = x 1 , X = x 2 . . . X = x n ) P(X=x_1,X=x_2...X=x_n) P(X=x1,X=x2...X=xn),也就是N个事件同时发生的概率
如果样本是离散型随机变量则: P = P ( X = x 1 ; θ ) P ( X = x 2 ; θ ) . . . P ( X = x n ; θ ) P= P(X=x_1;\theta)P(X=x_2;\theta)...P(X=x_n;\theta) P=P(X=x1;θ)P(X=x2;θ)...P(X=xn;θ)
如果样本是连续型随机变量则: P = f ( x 1 ; θ ) f ( x 2 ; θ ) . . . f ( x n ; θ ) P= f(x_1;\theta)f(x_2;\theta)...f(x_n;\theta) P=f(x1;θ)f(x2;θ)...f(xn;θ),其中f(x)为随机变量X的概率密度函数
则我们另似然函数为: L ( θ ) = ∏ i = 1 n f ( x i ; θ ) O R L ( θ ) = ∏ i = 1 n P ( X = x i ; θ ) L(\theta) =\prod_{i=1}^{n}f(x_i;\theta)\quad OR\quad L(\theta) =\prod_{i=1}^{n}P(X=x_i;\theta) L(θ)=∏i=1nf(xi;θ)ORL(θ)=∏i=1nP(X=xi;θ)
累乘函数显然不易于求导,则我们对似然函数去对数则: l n ( L ( θ ) ) = ∑ i = 1 n l n [ f ( x i ; θ ) ] O R ∑ i = 1 n l n [ P ( X = x i ; θ ) ] ln(L(\theta)) = \sum_{i=1}^{n}ln[f(x_i;\theta)] \quad OR\quad \sum_{i=1}^{n}ln[P(X=x_i;\theta)] ln(L(θ))=∑i=1nln[f(xi;θ)]OR∑i=1nln[P(X=xi;θ)]
为了求似然函数的最大值我们对似然函数进行求导,进而考虑单调性,比较驻点和边界点的值从而取到似然函数的最大值,由 d l n L ( θ ) d θ = 0 \frac{dlnL(\theta)}{d \theta}=0 dθdlnL(θ)=0,求解出 θ \theta θ的表达式,进而代入样本值得到参数的极大似然估计。
1.7朴素贝叶斯所属分类
根据《统计学习方法》中对机器学习的分类方法,我们可以了解到朴素贝叶斯属于监督学习,以及参数化模型,同时由于它的模型是虽然学习先验概率和条件概率但目标是为了学习联合概率分布,所以朴素贝叶斯属于概率模型和生成模型,同时朴素贝叶斯是为了解决监督学习中的分类问题。
2.模型
输入,输出,目标
输入:X= { x 1 ( m ) , x 2 ( m ) . . . x n ( m ) , y ( m ) } T {\{x^{(m)}_1,x^{(m)}_2...x^{(m)}_n,y^{(m)}\}}^T {x1(m),x2(m)...xn(m),y(m)}T
输出:Y= { C 1 , C 2 . . . C k } \{C_1,C_2...C_k\} {C1,C2...Ck}
目标:给定一个新的特征向量判断它是属于Y中哪个类型的,或者说它属于哪个类型的概率最大。
方法:利用数据学习 P ( X / Y ) 和 P ( Y ) P(X/Y)和P(Y) P(X/Y)和P(Y),得到联合概率分布,再利用贝叶斯定理与学到的联合概率模型进行分类预测,选出概率最大的类型: P ( Y / X ) = P ( X , Y ) P ( X ) = P ( Y ) P ( X / Y ) ∑ Y P ( Y ) P ( X / Y ) P(Y/X)=\frac{P(X,Y)}{P(X)}= \frac{P(Y)P(X/Y)}{\sum^{Y}P(Y)P(X/Y)} P(Y/X)=P(X)P(X,Y)=∑YP(Y)P(X/Y)P(Y)P(X/Y)
3.策略与算法
3.1学习 P ( Y ) P(Y) P(Y)
在朴素贝叶斯算法中 P ( Y ) P(Y) P(Y),也就是先验概率分布是通过极大似然估计法来估计每一个 Y = C k Y=C_k Y=Ck的概率P:
假设
P
(
Y
=
C
k
)
=
p
P(Y=C_k)=p
P(Y=Ck)=p,则
P
(
Y
!
=
C
k
)
=
1
−
p
P(Y!=C_k)=1-p
P(Y!=Ck)=1−p,显然n个样本就可以理解为n次独立同分布的伯努利实验,为了方便计数我们引入指示函数:
I
(
Y
)
=
{
Y
=
=
C
k
?
1
:
0
}
I(Y)=\{Y==C_k ? 1 : 0\}
I(Y)={Y==Ck?1:0},则离散型随机变量最大似然函数估计的过程为:
∵
L
(
p
)
=
∏
i
=
1
n
P
(
Y
;
p
)
=
p
∑
i
=
1
n
I
(
y
i
)
∗
(
1
−
p
)
n
−
∑
i
=
1
n
I
(
y
i
)
∴
l
n
(
L
(
p
)
)
=
∑
i
=
1
n
I
(
y
i
)
l
n
(
p
)
+
[
n
−
∑
i
=
1
n
I
(
y
i
)
]
l
n
(
1
−
p
)
∵
∂
l
n
(
L
(
p
)
)
∂
p
=
∑
i
=
1
n
I
(
y
i
)
p
+
n
−
∑
i
=
1
n
I
(
y
i
)
1
−
p
=
0
∴
(
1
−
p
)
∑
i
=
1
n
I
(
y
i
)
=
p
(
n
−
∑
i
=
1
n
I
(
y
i
)
)
n
p
=
∑
i
=
1
n
I
(
y
i
)
∴
p
=
∑
i
=
1
n
I
(
y
i
)
n
\because L(p) = \prod_{i=1}^{n}P(Y;p)=p^{ \sum_{i=1}^n I(y_i)}*(1-p)^{n -\sum_{i=1}^n I(y_i) }\\ \therefore ln(L(p)) = \sum_{i=1}^n I(y_i) ln(p) + [n -\sum_{i=1}^n I(y_i)]ln(1-p)\\ \because\frac{\partial ln(L(p)) }{\partial p} = \frac{ \sum_{i=1}^n I(y_i)}{p} + \frac{ n -\sum_{i=1}^n I(y_i)}{1-p}=0\\ \therefore (1-p)\sum_{i=1}^n I(y_i) = p( n -\sum_{i=1}^n I(y_i))\\ np = \sum_{i=1}^n I(y_i)\\ \therefore p=\frac{ \sum_{i=1}^n I(y_i)}{n}
∵L(p)=i=1∏nP(Y;p)=p∑i=1nI(yi)∗(1−p)n−∑i=1nI(yi)∴ln(L(p))=i=1∑nI(yi)ln(p)+[n−i=1∑nI(yi)]ln(1−p)∵∂p∂ln(L(p))=p∑i=1nI(yi)+1−pn−∑i=1nI(yi)=0∴(1−p)i=1∑nI(yi)=p(n−i=1∑nI(yi))np=i=1∑nI(yi)∴p=n∑i=1nI(yi)
最大似然估计的结果从数值上理解就是在n个样本中,若
Y
=
C
k
Y=C_k
Y=Ck 的个数为m,则
Y
=
C
k
Y=C_k
Y=Ck的概率为
m
n
\frac{m}{n}
nm,也就是:
P
(
Y
=
C
k
)
=
m
n
P(Y=C_k) = \frac{m}{n}
P(Y=Ck)=nm
3.2学习条件概率 P ( X = x / Y = C k ) P(X=x/Y=C_k) P(X=x/Y=Ck)
我们假设 P ( X = x / Y = C k ) = P ( X 1 = x 1 , X 2 = x 2 . . . X n = x n / Y = C k ) P(X=x/Y=C_k) =P(X_1 = x_1,X_2= x_2...X_n=x_n/Y=C_k) P(X=x/Y=Ck)=P(X1=x1,X2=x2...Xn=xn/Y=Ck)这个条件概率可以表示为在 Y = C k Y=C_k Y=Ck的条件下,一个X样本的概率为多少
则上式就等价于: P ( X 1 = x 1 ∩ X 2 = x 2 ∩ . . . ∩ X n = x n / Y = C k ) P(X_1 = x_1\cap X_2= x_2 \cap ...\cap X_n=x_n/Y=C_k) P(X1=x1∩X2=x2∩...∩Xn=xn/Y=Ck)
我们假设一个特征 x i x_i xi的取值有 S j S_j Sj个,则如果我们按照多项式分布的思想,算X向量某一取值就需要计算 ∏ i = 1 n S j \prod_{i=1}^nS_j ∏i=1nSj次去进行参数估计,如果再加上条件概率就需要计算 k ∏ i = 1 n S j k\prod_{i=1}^nS_j k∏i=1nSj次,这合理吗?这显然不合理,如果在1000维特征的算法中,这种规模的计算太浪费时间了。
贝叶斯学派大胆的做了一个强假设(只有在特定情况才会精准的假设):假设X的每一个特征之间独立,这就使得式子简化为:
P
(
X
1
=
x
1
∩
X
2
=
x
2
∩
.
.
.
∩
X
n
=
x
n
/
Y
=
C
k
)
=
P
(
X
=
x
1
/
Y
=
C
k
)
P
(
X
=
x
2
/
Y
=
C
k
)
.
.
.
P
(
X
=
x
n
/
Y
=
C
k
)
=
∏
i
=
1
n
P
(
X
=
x
i
/
Y
=
C
k
)
P(X_1 = x_1\cap X_2= x_2 \cap ...\cap X_n=x_n/Y=C_k) \\=P(X=x_1/Y=C_k)P(X=x_2/Y=C_k)...P(X=x_n/Y=C_k) \\=\prod_{i=1}^n P(X=x_i/Y=C_k)
P(X1=x1∩X2=x2∩...∩Xn=xn/Y=Ck)=P(X=x1/Y=Ck)P(X=x2/Y=Ck)...P(X=xn/Y=Ck)=i=1∏nP(X=xi/Y=Ck)
这是不是就极大的简化了运算量,但是朴素贝叶斯算法的弊端就体现在这,我们对这个假设再进行一次深度的理解,什么叫做:X的每一个特征之间独立,这就意味着每一个特征之间互不干扰,是独自发展起来的,举个栗子来说就是:你胳膊的长度,你腿的长度,你的身高这三个特征是各自发育起来的,你可能只有1.8m但是你的胳膊有3m,这是不是很不合理。是的这也是贝叶斯学派备受争议的地方,但是这种不合理的方法一定无用吗?
并不是这样的,当X的特征之间依赖不强时,比如说我们对一个奇葩人偶展的人偶进行概率统计计算,由于它的每一个部分是单独制作出来最后组装起来的,各部分之间并没有强相关性,这个时候的这种假设就属于非常满足的情况,那我们考虑现实的实际的情况:
如果特征之间相关度不高,我们可以牺牲一部分结果的准确性来提高计算的效率。这并不是随意的,没有依据的假设,而是可以严格科学论证的假设,由于我们运用模型的最终目的是为了提高效率,并且最优化解法也只是理论最优,在假设空间中最趋近于最优解的解,那么我们在计算时牺牲一部分的精确度来提高计算的效率这种思想时非常合理的。
从经验来看,朴素贝叶斯在小规模数据中具有更快的收敛性,也就是效率更高。
3.3后验概率最大化
回到我们最终的目标,我们的最终目标是计算后验概率 P ( Y = C k / X ) P(Y=C_k/X) P(Y=Ck/X),为什么这样说,因我们的根本目标是为了给定一个X特征向量,然后通过模型,计算出X属于哪个 C k C_k Ck的概率最大,我们会计算出k个 P k = P ( Y = C k / X ) P_k = P(Y=C_k/X) Pk=P(Y=Ck/X),我们只要取其中最大的P所对应的 C k C_k Ck即可。
代入贝叶斯定理:
P
(
Y
=
C
k
/
X
)
=
P
(
Y
=
C
k
,
X
)
P
(
X
)
=
P
(
X
=
x
/
Y
=
C
k
)
P
(
Y
=
C
k
)
P
(
X
)
=
P
(
X
=
x
/
Y
=
C
k
)
P
(
Y
=
C
k
)
∑
i
=
1
k
P
(
X
=
x
/
Y
=
C
k
)
P
(
Y
=
C
k
)
P(Y=C_k/X) = \frac{P(Y=C_k,X)}{P(X)} \\=\frac{ P(X=x/Y=C_k)P(Y=C_k)}{P(X)} \\=\frac{ P(X=x/Y=C_k)P(Y=C_k)}{\sum_{i=1}^k P(X=x/Y=C_k)P(Y=C_k)}
P(Y=Ck/X)=P(X)P(Y=Ck,X)=P(X)P(X=x/Y=Ck)P(Y=Ck)=∑i=1kP(X=x/Y=Ck)P(Y=Ck)P(X=x/Y=Ck)P(Y=Ck)
代入上面学习出的模型:
P
(
X
=
x
/
Y
=
C
k
)
=
∏
i
=
1
n
P
(
X
=
x
i
/
Y
=
C
k
)
P(X=x/Y=C_k) = \prod_{i=1}^n P(X=x_i/Y=C_k)
P(X=x/Y=Ck)=∏i=1nP(X=xi/Y=Ck)
原式就等于:
=
∏
i
=
1
n
P
(
X
=
x
i
/
Y
=
C
k
)
P
(
Y
=
C
k
)
∑
i
=
1
k
∏
i
=
1
n
P
(
X
=
x
i
/
Y
=
C
k
)
P
(
Y
=
C
k
)
=\frac{ \prod_{i=1}^n P(X=x_i/Y=C_k) P(Y=C_k)} {\sum_{i=1}^k \prod_{i=1}^n P(X=x_i/Y=C_k)P(Y=C_k)}
=∑i=1k∏i=1nP(X=xi/Y=Ck)P(Y=Ck)∏i=1nP(X=xi/Y=Ck)P(Y=Ck)
则朴素贝叶斯分类器就可以表示为:
y
=
f
(
x
)
=
a
r
g
m
a
x
C
k
[
∏
i
=
1
n
P
(
X
=
x
i
/
Y
=
C
k
)
P
(
Y
=
C
k
)
∑
i
=
1
k
∏
i
=
1
n
P
(
X
=
x
i
/
Y
=
C
k
)
P
(
Y
=
C
k
)
]
y=f(x)=argmax_{C_k}[\frac{ \prod_{i=1}^n P(X=x_i/Y=C_k) P(Y=C_k)} {\sum_{i=1}^k \prod_{i=1}^n P(X=x_i/Y=C_k)P(Y=C_k)}]
y=f(x)=argmaxCk[∑i=1k∏i=1nP(X=xi/Y=Ck)P(Y=Ck)∏i=1nP(X=xi/Y=Ck)P(Y=Ck)]
显然对于f(x)所对应的k个概率,分母都是相同的,所以我们可以进一步的简化这个式子:
y
=
f
(
x
)
=
a
r
g
m
a
x
C
k
[
∏
i
=
1
n
P
(
X
=
x
i
/
Y
=
C
k
)
P
(
Y
=
C
k
)
]
y=f(x)=argmax_{C_k} [\prod_{i=1}^n P(X=x_i/Y=C_k) P(Y=C_k)]
y=f(x)=argmaxCk[i=1∏nP(X=xi/Y=Ck)P(Y=Ck)]

