当前位置：首页 > article >正文

[NOIP2008 普及组] 排座椅

article 2024/11/6 12:42:32

题目描述

上课的时候总会有一些同学和前后左右的人交头接耳，这是令小学班主任十分头疼的一件事情。不过，班主任小雪发现了一些有趣的现象，当同学们的座次确定下来之后，只有有限的D对同学上课时会交头接耳。

同学们在教室中坐成了M行N列，坐在第i行第j列的同学的位置是 (i,j)，为了方便同学们进出，在教室中设置了K条横向的通道，L条纵向的通道。

于是，聪明的小雪想到了一个办法，或许可以减少上课时学生交头接耳的问题：她打算重新摆放桌椅，改变同学们桌椅间通道的位置，因为如果一条通道隔开了2个会交头接耳的同学，那么他们就不会交头接耳了。

请你帮忙给小雪编写一个程序，给出最好的通道划分方案。在该方案下，上课时交头接耳的学生的对数最少。

输入格式

第一行，有5个用空格隔开的整数，分别是 M,N,K,L,D(2≤N,M≤1000,0≤K<M,0≤L<N,D≤2000)。

接下来的D行，每行有4个用空格隔开的整数。第i行的4个整数 Xi,Yi,Pi,Qi，表示坐在位置(Xi,Yi)与(Pi,Qi)的两个同学会交头接耳（输入保证他们前后相邻或者左右相邻）。

输入数据保证最优方案的唯一性。

输出格式

共两行。
第一行包含K个整数a1,a2,…,aK，表示第a1行和a1+1行之间、第a2 行和a2+1行之间、…、第aK行和第aK+1 行之间要开辟通道，其中ai<ai+1，每两个整数之间用空格隔开（行尾没有空格）。

第二行包含L个整数b1,b2,…,bL，表示第b1列和b1+1列之间、第b2列和b2+1列之间、…、第bL列和第bL+1列之间要开辟通道，其中bi<bi+1，每两个整数之间用空格隔开（列尾没有空格）。

输入数据 1

输出数据 1

2
2 4

提示

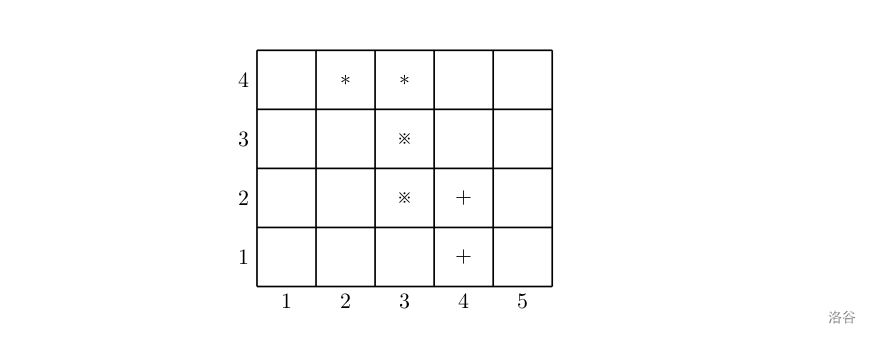
上图中用符号*、※、+标出了3对会交头接耳的学生的位置，图中3条粗线的位置表示通道，图示的通道划分方案是唯一的最佳方案。

来源

2008 年普及组第二题

代码

#include<bits/stdc++.h>
using namespace std;
struct A{
	int n1,p1;
}k[1005],l[1005];
bool cmp(A xx,A yy){
	return xx.n1>yy.n1;
}
bool cmp1(A xxx,A yyy){
	return xxx.p1<yyy.p1;
}
int main(){
	int m,n,p,q,d,x1,y1,x2,y2;
    cin>>m>>n>>p>>q>>d;
    for(int i=1;i<=d;i++){
        cin>>x1>>y1>>x2>>y2;
        if(x1==x2){
        	l[min(y1,y2)].p1=min(y1,y2);
        	l[min(y1,y2)].n1++;
		}else{
			k[min(x1,x2)].p1=min(x1,x2);
        	k[min(x1,x2)].n1++;
		}
    }
    sort(l+1,l+n+1,cmp);
    sort(k+1,k+m+1,cmp);
    sort(l+1,l+q+1,cmp1);
    sort(k+1,k+p+1,cmp1);
    for(int i=1;i<=p;i++)cout<<k[i].p1<<' ';
    cout<<'\n';
    for(int i=1;i<=q;i++)cout<<l[i].p1<<' ';
    return 0;
}