034_Structural_Transient_In_Matlab结构动力学问题求解

结构动态问题

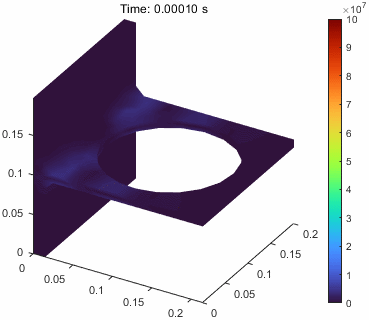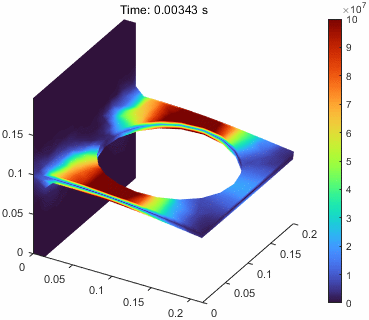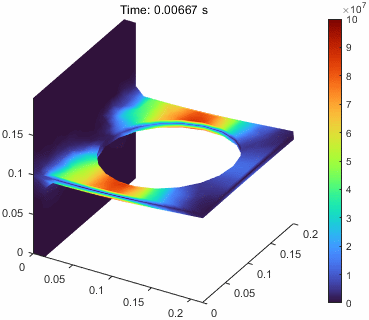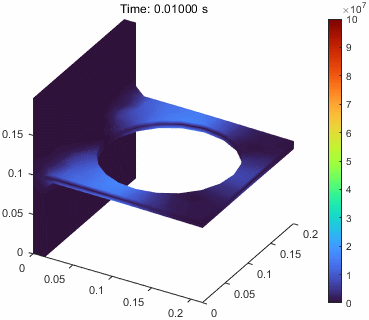
问题描述

我们试着给前面已经做过的问题上加一点有趣的东西。

• 结构静力学求解

当时求解这个问题，在最外面的竖直切面加载了一个静态的固定的力。下面我们试试看在上方的表面增加一个脉冲压力载荷。

采用统一的有限元框架，定义问题，几何体已经出现过一次。

%% Rectangular Pressure Pulse on Boundary

% Create a model and include the bracket geometry.
model = femodel(AnalysisType="structuralTransient", ...
    Geometry="BracketWithHole.stl");

pdegplot(model.Geometry, 'FaceLabels', 'on', 'FaceAlpha', 0.5);

​

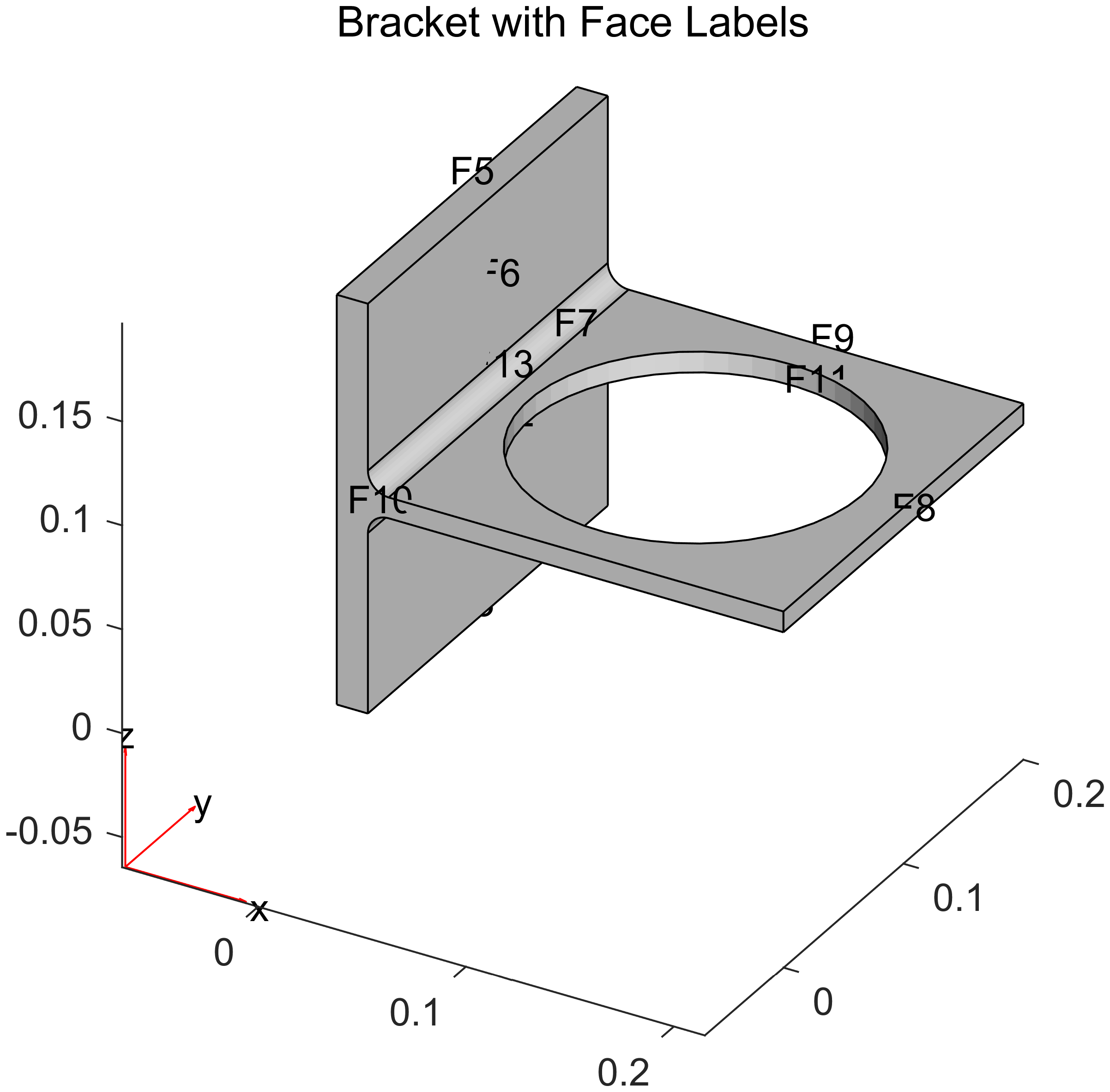
材料特性设置。

% Specify Young's modulus, Poisson's ratio, and mass density.
model.MaterialProperties = ...
    materialProperties(YoungsModulus=200e9, ...
    PoissonsRatio=0.3, MassDensity=7800);

​

边界与加载

边界条件

首先是固定表面，我们把最大的竖直表面固定起来。

% Specify that face 4 is a fixed boundary.
model.FaceBC(4) = faceBC(Constraint="fixed");

​

注意，我们这里设置边界条件的函数，由小写字母开头，而设置好的边界条件的变量，首字母是大写的。通过在faceBC中的Name=Value可以设置边界条件的值。

可以查看faceBC的帮助。

help faceBC

 faceBC - Boundary conditions on geometry face
    A faceBC object specifies the type of boundary condition on a face of a
    geometry.

    创建
      语法
        model.FaceBC(FaceID) = faceBC(Name=Value)

      输入参数
        FaceID - Face IDs
          vector of positive integers

    属性
      Constraint - Standard structural boundary constraints
        "fixed"
      XDisplacement - x-component of enforced displacement
        real number | function handle
      YDisplacement - y-component of enforced displacement
        real number | function handle
      ZDisplacement - z-component of enforced displacement
        real number | function handle
      Temperature - Temperature boundary condition
        real number | function handle
      Voltage - Voltage
        real number | function handle
      ElectricField - Electric field
        column vector | function handle
      MagneticField - Magnetic field
        column vector | function handle
      MagneticPotential - Magnetic potential
        real number | column vector | function handle
      FarField - Absorbing region
        farFieldBC object

    示例
      openExample('pde/FixedBoundariesExample')
      openExample('pde/BoundaryConditionsFor3DHarmonicElectromagneticAnalysisExample')

    另请参阅 femodel, fegeometry, farFieldBC, edgeBC, vertexBC, cellLoad,
      faceLoad, edgeLoad, vertexLoad

    已在 R2023a 中的 Partial Differential Equation Toolbox 中引入
    faceBC 的文档
       doc faceBC

​
​
​

接下来就是这个比较难的脉冲加载。

加载的设置方法，类似于边界条件的设置。可以设置不同的选择，例如，对于结构问题：

• Pressure：垂直于面的压力载荷，单位为Pa
• SurfaceTraction：表面载荷，力，单位为N

% Apply a rectangular pressure pulse on face 7 in the direction normal to the face.
pressurePulse = @(location,state) ...
    rectangularLoad(10^5,location,state,[0.0 0.002]);
model.FaceLoad(7) = faceLoad(Pressure=pressurePulse);

​

这里的问题，脉冲载荷如何实现？

脉冲加载

在faceLoad函数的Name=Value中，值可以采取多种形式，主要我们用到的是数值和函数。

当这里使用一个函数是， 对函数的输入和输出有固定的要求。

• 输入1：位置，一般称为location
• 输入2: 状态

function value = loadFucntion(location, state)

end

这个函数的两个参数分别是位置和状态，是两个结构体，其具体内容如下：

• location — 结构体，包含以下字段：:
  • location.x — x坐标，是一个点或者若干个点
  • location.y — y坐标，是一个点或者若干个点
  • location.z — z坐标，是一个点或者若干个点
  • location.nx — 法向量的x分量，是一个点的或者若干个点的
  • location.ny — 法向量的y分量，是一个点的或者若干个点的
  • location.nz — 法向量的z分量，是一个点的或者若干个点的
• state — 对于非线性问题和动态问题才有意义，包括以下字段的结构体：
  • state.u — 对应与location中定义点的状态变量（对于结构问题，就是位移）
  • state.ux — 估计的导数x分量
  • state.uy — 估计的导数y分量
  • state.uz — 估计的导数y分量
  • state.time — 时间
  • state.frequency — 频率
  • state.NormFluxDensity — 非线性磁场问题才需要的参数

对于我们想要求解的脉冲压力载荷问题，我们定义一个方波脉冲，这个方波脉冲的参数包括：

1. load，载荷大小
2. T，载荷时间，一个数组，包含两个时间点，分别是载荷开始和结束的时间

function Tn = rectangularLoad(load,location,state,T)
if isnan(state.time)
    Tn = NaN*(location.nx);
    return
end
if isa(load,"function_handle")
    load = load(location,state);
else
    load = load(:);
end
% Two time-points that define a rectangular pulse
T1 = T(1); % Start time
T2 = T(2); % End time

% Determine multiplicative factor for the specified time.
TnTrap = max([(state.time - T1)*(T2 - state.time)/ ...
    abs((state.time - T1)*(T2 - state.time)),0]);
Tn = load.* TnTrap;
end

最后这个TnTrap是一个方波函数，其值在T1和T2之间为1，其他地方为0。

因为这里我们是一个时变问题，所以用到了state.time，这个是时间。

现在回到我们的设置中：

pressurePulse = @(location,state) ...
    rectangularLoad(10^5,location,state,[0.0 0.002]);

我们用上面方波函数定义了一个载荷函数，大小为$10^5$，载荷时间为0到0.002s。

求解

接下来就是网格和求解。

% Generate a mesh and assign it to the model.
model = generateMesh(model);

% pdemesh(model);

% 也可以是

pdeplot3D(model.Geometry.Mesh);

​

​

​

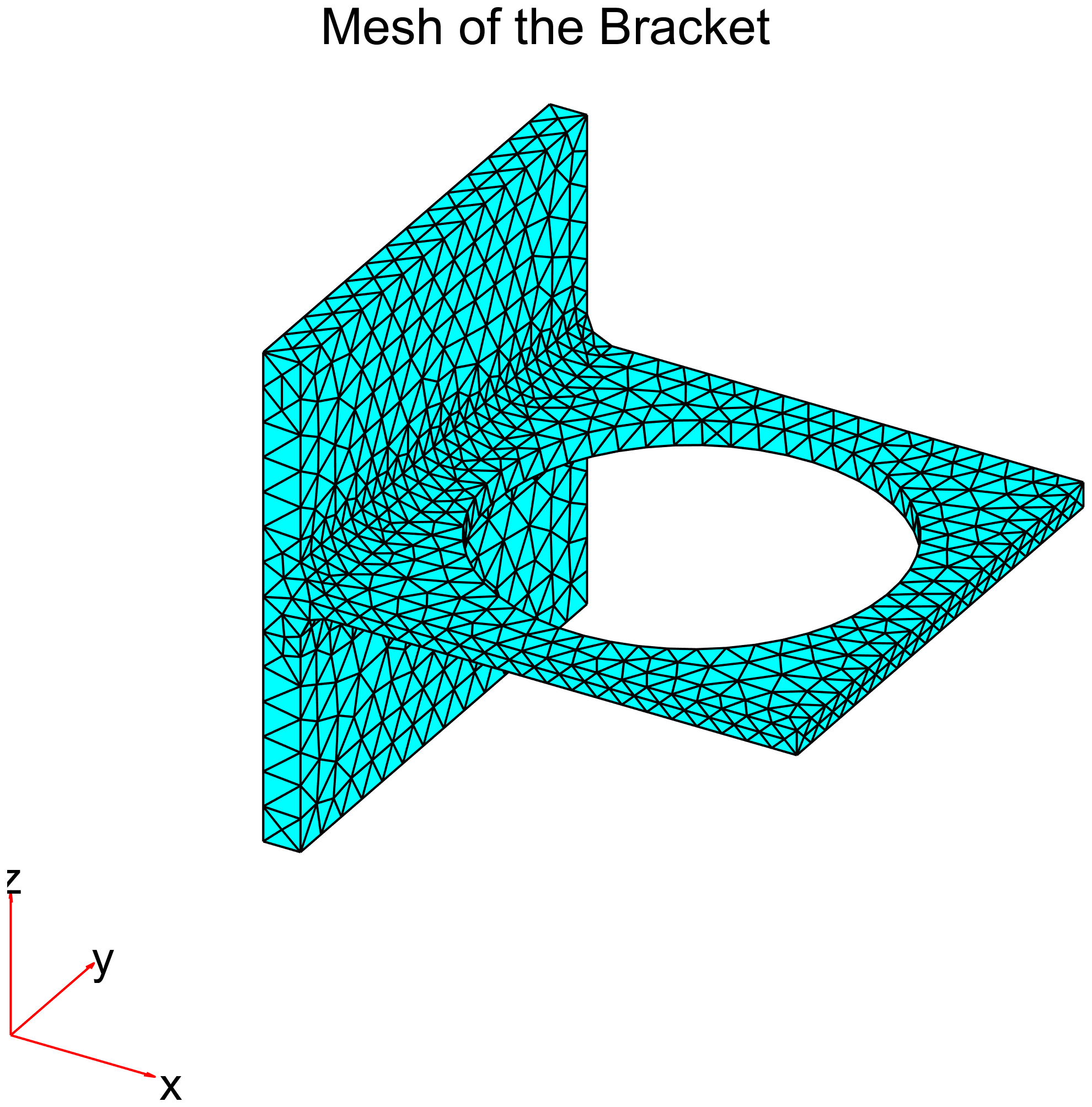
求解要针对一个时间序列，这里我们设置时间序列为0到0.01s，取100个点。尽量分辨脉冲的宽度0.002s。

% Solve the problem.
result = solve(model,linspace(0,0.01,100));

​

可视化

前面我们利用pdeplot3D函数进行可视化，这个函数可以把求解的结果映射到网络结构上，对点、线、面进行着色。在前面两个结构静力学的例子中都得到应用。

这里，因为是一个动态问题，我们实际更想要更好地理解在动态载荷下，结构是如何发生变形和位移的。

这里我们就要介绍一个新的函数pdeviz，这个函数提供了更多的可视化功能，可以对结构的变形、位移、应力、应变等进行可视化。

另外，在动态问题的结果中，我们看看，结果包含了哪些内容：

result

result = 

  TransientStructuralResults - 属性:

     Displacement: [1x1 FEStruct]
         Velocity: [1x1 FEStruct]
     Acceleration: [1x1 FEStruct]
    SolutionTimes: [0 1.0101e-04 2.0202e-04 3.0303e-04 4.0404e-04 5.0505e-04 6.0606e-04 7.0707e-04 8.0808e-04 ... ] (1x100 double)
             Mesh: [1x1 FEMesh]

​
​

那么我们要用应力来着色，还需要用到一系列专门给输出利用的函数，这些函数都用evaluate开头。

• evaluateStress 动态结构问题的应力评估
• evaluateStrain 动态结构问题的应变评估
• evaluateVonMisesStress 动态结构问题的von Mises应力评估

此外，还有下面的几个函数：

• evaluateReaction 评估边界的反作用力
• evaluatePrincipalStress 评估节点位置的主应力
• evaluatePrincipalStrain 评估节点位置的主应变

有上述函数的帮助，我们可以构造一个动态过程的可视化。

fn = "structuralDyanmicLoad-viz.gif";
if isfile(fn)
    delete(fn)
end


vmStress = evaluateVonMisesStress(result);

v = pdeviz(model.Geometry.Mesh);
v.MeshVisible = "off";
v.AxesVisible = "on";
v.DeformationScaleFactor = 10;

for i = 2:numel(result.SolutionTimes)
    % pdeplot3D(result.Mesh, ColorMapData=result.Displacement.uz(:,i))
    title(sprintf("Time: %.5f s",result.SolutionTimes(i)))
    
    v.NodalData = vmStress(:, i);
    v.DeformationData = ...
        struct('ux', result.Displacement.ux(:, i), ...
            'uy', result.Displacement.uy(:, i), ...
            'uz', result.Displacement.uz(:, i));    
    
    % specificy fixed color limits
    clim([0, 1e8])
    
    exportgraphics(gcf, fn, Append=true, Resolution=80)
end

当然这里的位移是进行整体放大的，v.DeformationScaleFactor = 10;，这个可以调整。

完整代码

完整的代码如下：

%% Rectangular Pressure Pulse on Boundary

% Create a model and include the bracket geometry.
model = femodel(AnalysisType="structuralTransient", ...
    Geometry="BracketWithHole.stl");

% Specify Young's modulus, Poisson's ratio, and mass density.
model.MaterialProperties = ...
    materialProperties(YoungsModulus=200e9, ...
    PoissonsRatio=0.3, MassDensity=7800);

% Specify that face 4 is a fixed boundary.
model.FaceBC(4) = faceBC(Constraint="fixed");

% By default, both the initial displacement and velocity are set to 0.

% Apply a rectangular pressure pulse on face 7 in the direction normal to the face.
pressurePulse = @(location,state) ...
    rectangularLoad(10^5,location,state,[0.0 0.002]);
model.FaceLoad(7) = faceLoad(Pressure=pressurePulse);

% Generate a mesh and assign it to the model.
model = generateMesh(model,Hmax=0.05);

% Solve the problem.
result = solve(model,linspace(0,0.01,100));


fn = "structuralDyanmicLoad-viz.gif";
if isfile(fn)
    delete(fn)
end


vmStress = evaluateVonMisesStress(result);

v = pdeviz(model.Geometry.Mesh);
v.MeshVisible = "off";
v.AxesVisible = "on";
v.DeformationScaleFactor = 10;

for i = 2:numel(result.SolutionTimes)
    % pdeplot3D(result.Mesh, ColorMapData=result.Displacement.uz(:,i))
    title(sprintf("Time: %.5f s",result.SolutionTimes(i)))
    
    v.NodalData = vmStress(:, i);
    v.DeformationData = struct('ux', result.Displacement.ux(:, i), ...
        'uy', result.Displacement.uy(:, i), ...
        'uz', result.Displacement.uz(:, i));
    
    
    % specificy fixed color limits
    clim([0, 1e8])
    
    exportgraphics(gcf, fn, Append=true, Resolution=80)
end