当前位置：首页 > article >正文

判断二叉搜索树（递归）

article 2024/11/8 1:30:52

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。binary search tree (BST)

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

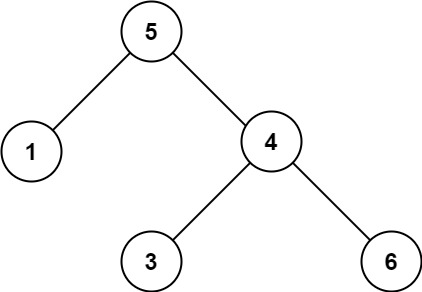
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

中序遍历：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    long long pre = LLONG_MIN; // 使用 long long 避免溢出
public:
   bool isValidBST(TreeNode* root) {
        if (!root) {
            return true;
        }
        if (!isValidBST(root->left) || root->val <= pre) {
            return false;
        }
        pre = root->val;  // 更新当前节点值
        return isValidBST(root->right);
    }
};

二叉搜索树进行中序遍历，得到的节点值应该是一个严格递增的序列。这意味着，只有当树是有效的二叉搜索树时，按中序遍历得到的值才会从小到大排列。

!isValidBST(root->left) :

递归检查左子树,如果左子树不是有效的二叉搜索树，返回 false。

root->val <= pre:

当前节点值必须大于前一个节点的值

实例：

5
/ \
3 7
/ \ / \
1 4 6 8

第1次递归：根节点 5

当前节点是 5，递归检查左子树。

第2次递归：节点 3

当前节点是 3，递归检查左子树。

第3次递归：节点 1

当前节点是 1，递归检查左子树（为空），返回 true。
节点 1 的值比 pre = LLONG_MIN 大，更新 pre = 1。
递归检查右子树（为空），返回 true。
节点 1 的子树符合 BST 条件，返回 true。

回到第2次递归：节点 3

当前节点是 3，递归检查右子树。

第4次递归：节点 4

当前节点是 4，递归检查左子树（为空），返回 true。
节点 4 的值比 pre = 1 大，更新 pre = 4。
递归检查右子树（为空），返回 true。
节点 4 的子树符合 BST 条件，返回 true。

回到第2次递归：节点 3

当前节点是 3，递归检查右子树（节点 4），返回 true。
节点 3 的值比 pre = 4 小，因此返回 false，树不符合 BST 条件。

后序遍历：

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        return isV(root, LONG_MIN, LONG_MAX);
    }
    
    bool isV(TreeNode* root, long min, long max) {
        if (!root) return true;  // 空节点是有效的
        
        if (root->val <= min || root->val >= max) {
            return false;  // 当前节点值不在有效范围内
        }
        
        return isV(root->left, min, root->val) && 
               isV(root->right, root->val, max);
    }
};

isV(root->left, min, root->val)

对左子树的值进行递归检查，更新右边界为当前节点的值

isV(root->right, root->val, max)

对右子树的值进行递归检查，更新左边界为当前节点的值