Leecode热题100-543.二叉树的直径

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

示例 1：

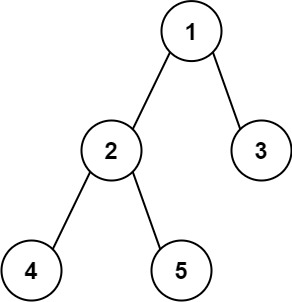
输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

输入：root = [1,2]
输出：1

提示：

• 树中节点数目在范围 [1, 104] 内
• -100 <= Node.val <= 100

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    /**题目的难度是简单，但是这个题其实个人认为是一个中等难度的题
    这个题用到的是二叉树的递归套路：一棵树的直径有以下的可能性：
    1.左树的直径  2. 右树的直径 3.包含根的情况下左右两个子树的以自己的根为结束点的最大长度
    因为我们要向每个节点要以下两个信息：1. 它的直径 2. 一定以根结束的情况下的最大长度，我们把这两个属性抽象出Info类 */
    public int diameterOfBinaryTree(TreeNode root) {
        Info info = getInfo(root);
        return info.diameter;
    }
    /**获取节点的Info信息的方法 */
    public Info getInfo(TreeNode root) {
        /**null就返回null吧，因为直径算的是距离而不是节点数量*/
        if(root == null) {
            return null;
        }
        /**这一步其实不用，但是为了少跑两次getInfo，这里写一下 */
        if(root.left == null && root.right == null) {
            return new Info(0,0);
        }
        /**拿到左右子树的信息 */
        Info leftInfo = getInfo(root.left);
        Info rightInfo = getInfo(root.right);
        /**定义当前节点的两个info属性 */
        int maxLenIncludeRoot = 0;
        int diameter = 0;
        /**题目要求的直径比较特殊，距离而不是节点数量
        所以我们这里需要判空一下，如果两个都不为空，用两个的信息组装，如果一个不为空，用一个的信息组装
        都为空的上面的if我们已经返回了*/
        if(leftInfo != null && rightInfo != null) {
            diameter = Math.max(leftInfo.diameter, Math.max(rightInfo.diameter, leftInfo.maxLenIncludeRoot + rightInfo.maxLenIncludeRoot + 2));
            maxLenIncludeRoot = Math.max(leftInfo.maxLenIncludeRoot, rightInfo.maxLenIncludeRoot) + 1;
        } else if(leftInfo != null) {
            diameter = Math.max(leftInfo.diameter, leftInfo.maxLenIncludeRoot + 1);
            maxLenIncludeRoot = leftInfo.maxLenIncludeRoot + 1;
        }  else {
            diameter = Math.max(rightInfo.diameter, rightInfo.maxLenIncludeRoot + 1);
            maxLenIncludeRoot = rightInfo.maxLenIncludeRoot + 1;
        }
        return new Info(diameter, maxLenIncludeRoot);
        
    }
    static class Info {
        int diameter;
        int maxLenIncludeRoot;
        public Info(int diameter, int maxLenIncludeRoot) {
            this.diameter = diameter;
            this.maxLenIncludeRoot = maxLenIncludeRoot;
        }
    }
}