当前位置： 首页 > article >正文

PyTorch nn.Embedding() 嵌入层详解和要点提醒

article 2024/11/13 4:01:41

在自然语言处理（NLP）任务中，我们需要把文本转换成一种机器能够“理解”的数字形式。通常，第一步是将文本进行分词（Tokenize），然后为每个词分配一个唯一的数字 ID，也就是 Token ID。这些 Token ID 可以输入到模型中，但需要明白的是，模型并不能直接从简单的数字中获取丰富的语义信息。类似于人类的认知，我们理解一个字或词并不是仅靠符号，而是其背后的含义。

“那么，如何让模型真正理解这些词语背后的含义呢？”

“既然一维的 Token ID 无法提供足够的信息，那就将其转换成更高维的向量，使其承载更丰富的语义信息，这就是嵌入层（Embedding Layer）的作用。”

代码文件下载

文章目录

  • nn.Embedding 嵌入层
    • 参数
    • 属性
    • 方法
      • 参数
  • 数学公式
  • 使用示例
  • 要点提醒
  • Q: 什么是语义？
  • 可视化
    • 环境配置
    • 导入
    • 加载预训练模型
    • 准备文本数据
    • 获取嵌入向量
    • 使用 t-SNE 降维
    • 画图
  • 参考链接
  • 附录
    • 可视化完整代码

nn.Embedding 嵌入层

torch.nn.Embedding(num_embeddings, embedding_dim, padding_idx=None, max_norm=None, norm_type=2.0, scale_grad_by_freq=False, sparse=False, _weight=None, _freeze=False, device=None, dtype=None)

A simple lookup table that stores embeddings of a fixed dictionary and size.

一个简单的查找表，用于存储固定大小的字典中每个词的嵌入向量。

参数

  • num_embeddings (int): 嵌入字典的大小，即词汇表的大小 (vocab size)。
  • embedding_dim (int): 每个嵌入向量的维度大小。
  • padding_idx (int, 可选): 指定填充（<PAD>）对应的索引值。padding_idx 对应的嵌入向量在训练过程中不会更新，即梯度不参与反向传播。对于新构建的 Embedding，padding_idx 处的嵌入向量默认为全零，但可以手动更新为其他值。
  • max_norm (float, 可选): 如果设置，嵌入向量的范数超过此值时将被重新归一化，使其范数等于 max_norm。
  • norm_type (float, 可选): 用于计算 max_norm 的 p-范数，默认为 2，即计算 2 范数。
  • scale_grad_by_freq (bool, 可选): 如果为 True，梯度将根据单词在 mini-batch 中的频率的倒数进行缩放，适用于高频词的梯度调整。默认为 False。
  • sparse (bool, 可选): 如果设置为 True，则权重矩阵的梯度为稀疏张量，适合大规模词汇表的内存优化。

属性

  • weight (Tensor): 模块的可学习权重，形状为 (num_embeddings, embedding_dim)，初始值从正态分布 N(0, 1) 中采样。

方法

from_pretrained(embeddings, freeze=True, padding_idx=None, max_norm=None, norm_type=2.0, scale_grad_by_freq=False, sparse=False)

Create Embedding instance from given 2-dimensional FloatTensor.

用于从给定的 2 维浮点张量（FloatTensor）创建一个 Embedding 实例，通俗来讲就是自定义二维的权重矩阵。

参数

  • embeddings (Tensor): 一个包含嵌入权重的 FloatTensor。第一个维度代表 num_embeddings（词汇表大小，vocab_size），第二个维度代表 embedding_dim（嵌入向量维度）。
  • freeze (bool, 可选): 如果为 True，则嵌入矩阵在训练过程中保持不变，相当于设置 embedding.weight.requires_grad = False。默认值为 True。
  • 其余参数参考之前定义。

数学公式

假设词汇表大小为 V V V，嵌入维度为 D D D，则嵌入层可以表示为一个矩阵 E ∈ R V × D E \in \mathbb{R}^{V \times D} E∈RV×D。

给定一个输入的 token ID 序列 { x 1 , x 2 , … , x n } \{x_1, x_2, \dots, x_n\} {x1​,x2​,…,xn​}，嵌入层的输出为对应的嵌入向量序列 { E x 1 , E x 2 , … , E x n } \{E_{x_1}, E_{x_2}, \dots, E_{x_n}\} {Ex1​​,Ex2​​,…,Exn​​}，其中每个 E x i ∈ R D E_{x_i} \in \mathbb{R}^D Exi​​∈RD。

嵌入层接受 x i x_i xi​ 作为输入，返回对应的行向量，公式如下：

E ( x i ) = E x i E(x_i) = E_{x_i} E(xi​)=Exi​​

其中, E E E 是嵌入矩阵, x i x_i xi​ 是输入的 token ID, E ( x i ) E(x_i) E(xi​) 是对应的嵌入向量。

使用示例

思考一个问题：对于神经网络来说，什么是“符号”及其“背后的含义”？

答：Token ID 和 Embedding。

运行代码理解 Embedding：

import torch
import torch.nn as nn

# 设置随机种子以确保结果可复现
torch.manual_seed(42)

# 定义嵌入层参数
num_embeddings = 5  # 假设词汇表中有 5 个 token
embedding_dim = 3   # 每个 token 对应 3 维嵌入向量

# 初始化嵌入层
embedding = nn.Embedding(num_embeddings, embedding_dim)

# 定义整数索引
input_indices = torch.tensor([0, 2, 4])

# 查找嵌入向量
output = embedding(input_indices)

# 打印结果
print("权重矩阵：")
print(embedding.weight.data)
print("\nEmbedding 输出：")
print(output)

输出：

权重矩阵：
tensor([[ 0.3367,  0.1288,  0.2345],
        [ 0.2303, -1.1229, -0.1863],
        [ 2.2082, -0.6380,  0.4617],
        [ 0.2674,  0.5349,  0.8094],
        [ 1.1103, -1.6898, -0.9890]])

Embedding 输出：
tensor([[ 0.3367,  0.1288,  0.2345],
        [ 2.2082, -0.6380,  0.4617],
        [ 1.1103, -1.6898, -0.9890]], grad_fn=<EmbeddingBackward0>)

在这个例子中，input_indices = [0, 2, 4]，嵌入层从权重矩阵中选择第 0、2 和 4 行，作为对应的嵌入表示。

可以看出，nn.Embedding 的核心功能就是根据索引从权重矩阵中查找对应的嵌入向量。

要点提醒

  1. 嵌入矩阵就是权重矩阵
    在 nn.Embedding 中，嵌入矩阵被视为模型的可学习参数 weight。在训练过程中，模型会根据损失函数调整嵌入矩阵，使其更好地表示词语的语义特征。
  2. nn.Embedding 实际上是一个查找表
    输入接受的是索引，返回权重矩阵中对应索引的行。以下是一个嵌入层的简单实现：
    class CustomEmbedding(nn.Module):
    def __init__(self, num_embeddings, embedding_dim):
        super(CustomEmbedding, self).__init__()
        self.weight = torch.nn.Parameter(torch.randn(num_embeddings, embedding_dim))
        
    def forward(self, indices):
        return self.weight[indices]  # 返回权重矩阵对应的行
  3. 嵌入层与线性层的区别
    嵌入层的权重矩阵形状为 (num_embeddings, embedding_dim)，即 (输入维度, 输出维度)，而线性层的权重矩阵形状为 (output_dim, input_dim)，即 (输出维度, 输入维度)，观察二者初始化时的差异：
    # Embedding
def __init__(self, num_embeddings, embedding_dim):
	self.weight = torch.nn.Parameter(torch.randn(num_embeddings, embedding_dim))

# Linear
def __init__(self, input_dim, output_dim):
    self.weight = nn.Parameter(torch.randn(output_dim, input_dim))
    self.bias = nn.Parameter(torch.randn(output_dim))
    嵌入层用于将离散的输入（如 Token ID）映射到连续的嵌入向量空间；线性层则进行线性变换。二者 forward() 的区别：
    # Embedding
def forward(self, input):
	return self.weight[input]

# Linear
def forward(self, input):
	torch.matmul(input, self.weight.T) + self.bias

    如果对线性层（nn.Linear）感兴趣，可以进一步阅读《深入理解全连接层：从线性代数到 PyTorch 中的 nn.Linear 和 nn.Parameter》。

  4. padding_idx 的作用
    假设在构造嵌入层时指定了 padding_idx=0，那么权重矩阵中第 0 行会被初始化为全零向量，并且在训练过程中不更新。
    示例：
    import torch
import torch.nn as nn

# 定义嵌入层，指定 padding_idx=0
embedding = nn.Embedding(num_embeddings=5, embedding_dim=3, padding_idx=0)

# 打印权重矩阵
print("权重矩阵：")
print(embedding.weight.data)
    输出：
    权重矩阵：
tensor([[ 0.0000,  0.0000,  0.0000],
        [-0.7658, -0.7506,  1.3525],
        [ 0.6863, -0.3278,  0.7950],
        [ 0.2815,  0.0562,  0.5227],
        [-0.2384, -0.0499,  0.5263]])
    可以看到，第 0 行是全零向量。
    验证 padding_idx 对应的嵌入是否在训练过程中保持不变：
    import torch
import torch.optim as optim

# 注意之前设置了 padding_idx=0
input_indices = torch.tensor([0, 2, 4])

# 定义一个简单的损失函数
loss_fn = nn.MSELoss()

# 目标值
target = torch.randn(3, 3)

# 定义优化器
optimizer = optim.SGD(embedding.parameters(), lr=0.1)

# 清空之前的梯度
optimizer.zero_grad()

# 前向传播
output = embedding(input_indices)

# 计算损失
loss = loss_fn(output, target)

# 反向传播，注意此时不会更新权重
loss.backward()

# 查看梯度
print("梯度：")
print(embedding.weight.grad)

# 打印权重矩阵
print("权重矩阵：")
print(embedding.weight.data)

# 更新权重
optimizer.step()

# 打印权重矩阵更新后
print("权重矩阵更新后:")
print(embedding.weight.data)
    输出：
    梯度：
tensor([[ 0.0000,  0.0000,  0.0000],
        [ 0.0000,  0.0000,  0.0000],
        [-0.0395,  0.1529,  0.3742],
        [ 0.0000,  0.0000,  0.0000],
        [-0.0863,  0.0353,  0.2030]])
原权重矩阵：
tensor([[ 0.0000,  0.0000,  0.0000],
        [-0.7658, -0.7506,  1.3525],
        [ 0.6863, -0.3278,  0.7950],
        [ 0.2815,  0.0562,  0.5227],
        [-0.2384, -0.0499,  0.5263]])
权重矩阵更新后:
tensor([[ 0.0000,  0.0000,  0.0000],
        [-0.7658, -0.7506,  1.3525],
        [ 0.6903, -0.3430,  0.7576],
        [ 0.2815,  0.0562,  0.5227],
        [-0.2297, -0.0534,  0.5060]])
    可以看到，padding_idx=0 对应的梯度为零，即在训练过程中不会更新。
  5. 使用预训练的嵌入向量
    有时候，我们希望使用预训练的嵌入（如 GloVe、Word2Vec）来初始化嵌入层。这时候可以使用 from_pretrained 方法：
    import torch
import torch.nn as nn

# 设置随机种子以确保结果可复现
torch.manual_seed(42)

# 假设我们有一个预训练的嵌入矩阵，这里只是随机初始化
pretrained_embeddings = torch.tensor(torch.randn(5, 3))

# 使用 from_pretrained 方法创建嵌入层，不冻结权重层（默认冻结）
embedding = nn.Embedding.from_pretrained(pretrained_embeddings, freeze=False)

# 查看权重矩阵
print("权重矩阵：")
print(embedding.weight.data)
    输出：
    权重矩阵：
tensor([[ 0.3367,  0.1288,  0.2345],
        [ 0.2303, -1.1229, -0.1863],
        [ 2.2082, -0.6380,  0.4617],
        [ 0.2674,  0.5349,  0.8094],
        [ 1.1103, -1.6898, -0.9890]])
    现在设置一下 padding_idx：
    embedding = nn.Embedding.from_pretrained(pretrained_embeddings, freeze=False, padding_idx=0)

# 查看权重矩阵
print("权重矩阵：")
print(embedding.weight.data)
    输出：
    权重矩阵：
tensor([[ 0.3367,  0.1288,  0.2345],
        [ 0.2303, -1.1229, -0.1863],
        [ 2.2082, -0.6380,  0.4617],
        [ 0.2674,  0.5349,  0.8094],
        [ 1.1103, -1.6898, -0.9890]])
    注意：虽然指定了 padding_idx=0，但预训练的嵌入矩阵第 0 行不会自动变为零向量。

上文“狭义”地解读了与 Token IDs 一起出现的 Embedding，这个概念在自然语言处理（NLP）中有着更具体的称呼：词嵌入（Word Embedding）。

Q: 什么是语义？

举个简单的例子来理解“语义”关系：像“猫”和“狗”在向量空间中的表示应该非常接近，因为它们都是宠物；“男人”和“女人”之间的向量差异可能代表性别的区别。此外，不同语言的词汇，如“男人”（中文）和“man”（英文），如果在相同的嵌入空间中，它们的向量也会非常接近，反映出跨语言的语义相似性。同时，【“女人”和“woman”（中文-英文）】与【“男人”和“man”（中文-英文）】之间的向量差异也可能非常相似。

可视化

环境配置

假设已经安装好了 PyTorch。

pip install transformers scikit-learn matplotlib seaborn

导入

import torch
from transformers import AutoTokenizer, AutoModel
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn.manifold import TSNE

加载预训练模型

# 选择预训练的 BERT 模型
model_name = 'bert-base-uncased'  # 对于中文模型，可使用 'bert-base-chinese'

# 加载分词器和模型
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModel.from_pretrained(model_name)

准备文本数据

words = ['cat', 'dog', 'apple', 'orange', 'king', 'queen', 'man', 'woman']

对于中文模型：

words = ['猫', '狗', '苹果', '橙子', '国王', '王后', '男人', '女人']

获取嵌入向量

实际上可以从模型中获取两种 Embedding：词嵌入（Word Embedding）和 句子嵌入（Sentence Embedding），分别对应方法一和方法二。

方法一：使用 BERT 的输入嵌入层

def get_input_embeddings(tokenizer, model, words):
    # 获取词表中的索引
    word_ids = [tokenizer.convert_tokens_to_ids(word) for word in words]
    # 从嵌入层提取对应的向量
    embeddings = model.embeddings.word_embeddings.weight[word_ids]
    return embeddings.detach().numpy()

方法二：使用 BERT 的输出嵌入

def get_output_embeddings(tokenizer, model, words):
    embeddings = []
    for word in words:
        inputs = tokenizer(word, return_tensors='pt')
        outputs = model(**inputs)
        # 获取 [CLS] 向量
        cls_embedding = outputs.last_hidden_state[0][0]  # [CLS] 的向量
        embeddings.append(cls_embedding.detach().numpy())
    return np.array(embeddings)

这里我们使用方法一：

embeddings = get_input_embeddings(tokenizer, model, words)

使用 t-SNE 降维

# 设置 t-SNE 参数
tsne = TSNE(n_components=2, perplexity=2, n_iter=1000, random_state=42)

# 执行降维
embeddings_2d = tsne.fit_transform(embeddings)

画图

plt.figure(figsize=(10, 10))
sns.scatterplot(x=embeddings_2d[:, 0], y=embeddings_2d[:, 1])

# 添加注释
for i, word in enumerate(words):
    plt.text(embeddings_2d[i, 0]+0.5, embeddings_2d[i, 1]+0.5, word)

plt.title('Word Embeddings Visualized using t-SNE')
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.show()

输出：

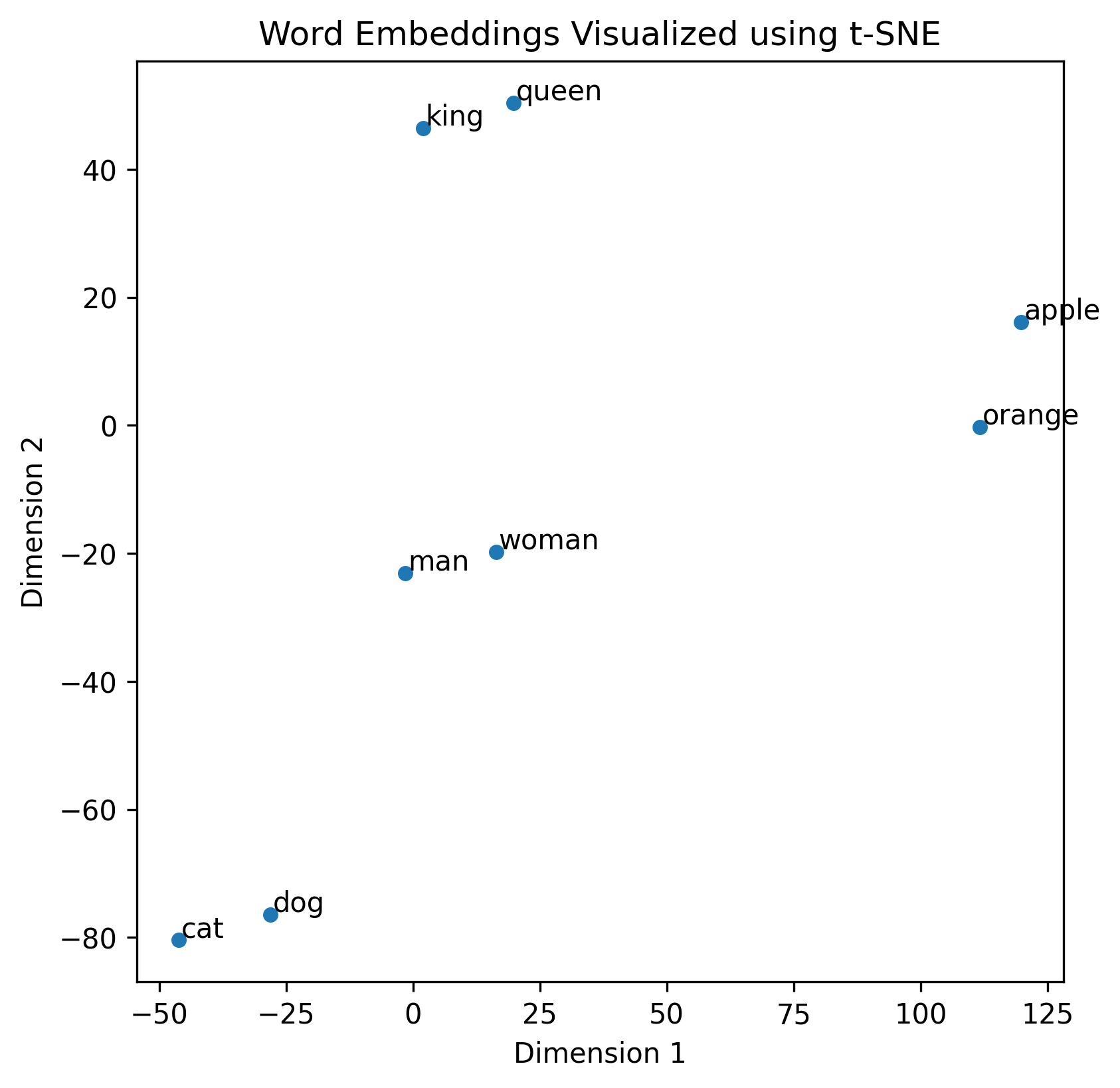
word_embeddings

参考链接

Embedding - Docs

附录

可视化完整代码

import torch
from transformers import AutoTokenizer, AutoModel
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn.manifold import TSNE

# 选择预训练的 BERT 模型
model_name = 'bert-base-uncased'  # 对于中文模型，可使用 'bert-base-chinese'

# 加载分词器和模型
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModel.from_pretrained(model_name)

# 要可视化的词语列表
words = ['cat', 'dog', 'apple', 'orange', 'king', 'queen', 'man', 'woman']
# words = ['猫', '狗', '苹果', '橙子', '国王', '王后', '男人', '女人']

def get_input_embeddings(tokenizer, model, words):
    # 获取词表中的索引
    word_ids = [tokenizer.convert_tokens_to_ids(word) for word in words]
    # 从嵌入层提取对应的向量
    embeddings = model.embeddings.word_embeddings.weight[word_ids]
    return embeddings.detach().numpy()

def get_output_embeddings(tokenizer, model, words):
    embeddings = []
    for word in words:
        inputs = tokenizer(word, return_tensors='pt')
        outputs = model(**inputs)
        # 获取 [CLS] 向量
        cls_embedding = outputs.last_hidden_state[0][0]  # [CLS] 的向量
        embeddings.append(cls_embedding.detach().numpy())
    return np.array(embeddings)

# 获取输入嵌入向量
embeddings = get_input_embeddings(tokenizer, model, words)

# 降维处理
tsne = TSNE(n_components=2, perplexity=2, n_iter=1000, random_state=42)
embeddings_2d = tsne.fit_transform(embeddings)

# 可视化
plt.figure(figsize=(10, 10))
sns.scatterplot(x=embeddings_2d[:, 0], y=embeddings_2d[:, 1])

for i, word in enumerate(words):
    plt.text(embeddings_2d[i, 0]+0.5, embeddings_2d[i, 1]+0.5, word)

plt.title('Word Embeddings Visualized using t-SNE')
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.show()

http://www.kler.cn/a/385680.html

相关文章：

  • 攻防世界37-unseping-CTFWeb
  • 基于STM32的智能充电桩：集成RTOS、MQTT与SQLite的先进管理系统设计思路
  • Xshell 7 偏好设置
  • 显示器接口种类 | 附图片
  • 【C++笔记】C++三大特性之继承
  • 论文1—《基于卷积神经网络的手术机器人控制系统设计》文献阅读分析报告
  • CSS3中的3D变换（3D空间与景深、透视点的位置、3D位移、3D旋转、3D缩放、3D多重交换、背部可见性）
  • 移动取证和 Android 安全
  • TCP（传输控制协议）和UDP（用户数据报协议）
  • uniapp 小程序 周选择器
  • 【机器学习】平均绝对误差（MAE：Mean Absolute Error）
  • stm32cubeide 1.16.1 在ubuntu 24.04上的安装
  • Intern大模型训练营（五）：书生大模型全链路开源体系笔记
  • Python代码主要实现了一个基于Transformer和LSTM的混合模型，用于对给定数据集进行二分类任务
  • 用 Python 从零开始创建神经网络（一）
  • MeterSphere接口自动化-ForEach循环
  • 五分钟使用 CocosCreator 快速部署 TON 游戏：开发基于 ZKP 的游戏
  • 【dvwa靶场：XSS系列】XSS (Stored)低-中-高级别，通关啦
  • 华为大咖说 | 浅谈智能运维技术
  • 【1】 Kafka快速入门-从原理到实践
  • 一七七、window.performance API使用介绍
  • SQL pta习题
  • 我谈正态分布——正态偏态
  • Stored procedures in PostgreSQL
  • C++入门基础知识142—【关于C++ 友元函数】
  • 国产操作系统ctyun下安装Informix SDK开发包的方法