数据结构和算法-贪心算法01- 认识贪心
贪心算法

什么是贪心算法
一个贪心算法总是做出当前最好的选择,也就是说,它期望通过局部最优选择从而得到全局最优的解决方案。
----《算法导论》
贪心算法(Greedy Method): 所谓贪心算法就是重复地(或贪婪地)根据一个法则挑选解的一部分。当挑选完毕时,最优解也就出现了。
贪心算法的几个核心问题
- 没有后悔药。一旦做出选择,不可以后悔。
- 有可能得到的不是最优解, 而是最优解的近似解。
- 选择什么样的贪心策略,直接决定算法的好坏。
解决贪心算法的策略
-
贪心策略
确定一个贪心策略,即选择一个好的方案。
-
局部最优解
一步一步地的到局部最优解。
-
全局最优解
将所有的局部最优解合成为原来问题的一个最优解。
tips: 想想我们的冒泡排序

贪心算法与动态规划算法的区别
贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择,不能回退。动态规划则会保存以前的运算结果,并根据以前的结果对当前进行选择,有回退功能。
再谈股票问题II
问题
[力扣122]122. 买卖股票的最佳时机 II - 力扣(LeetCode)
问题描述
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
最大总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0。
解决方案
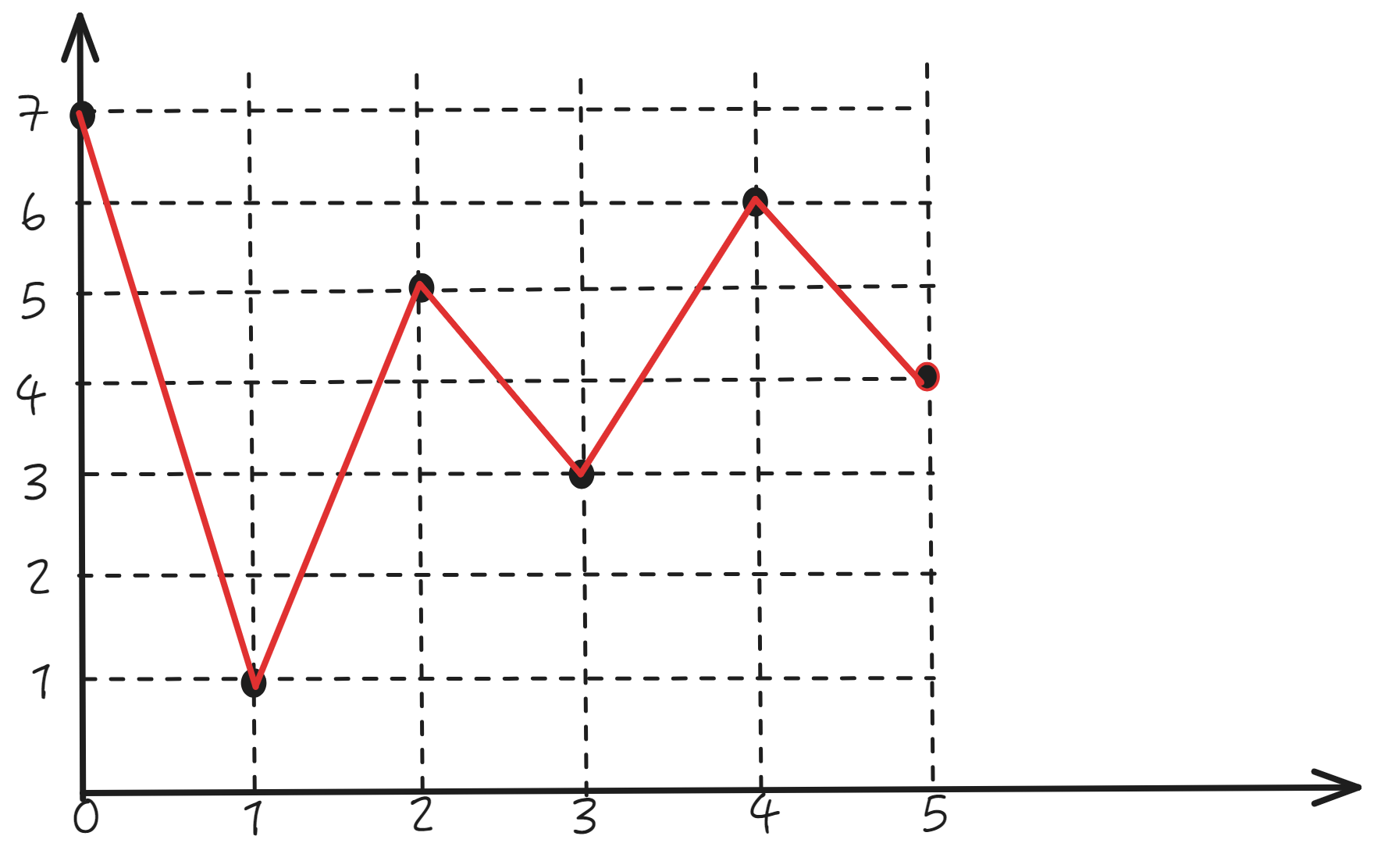
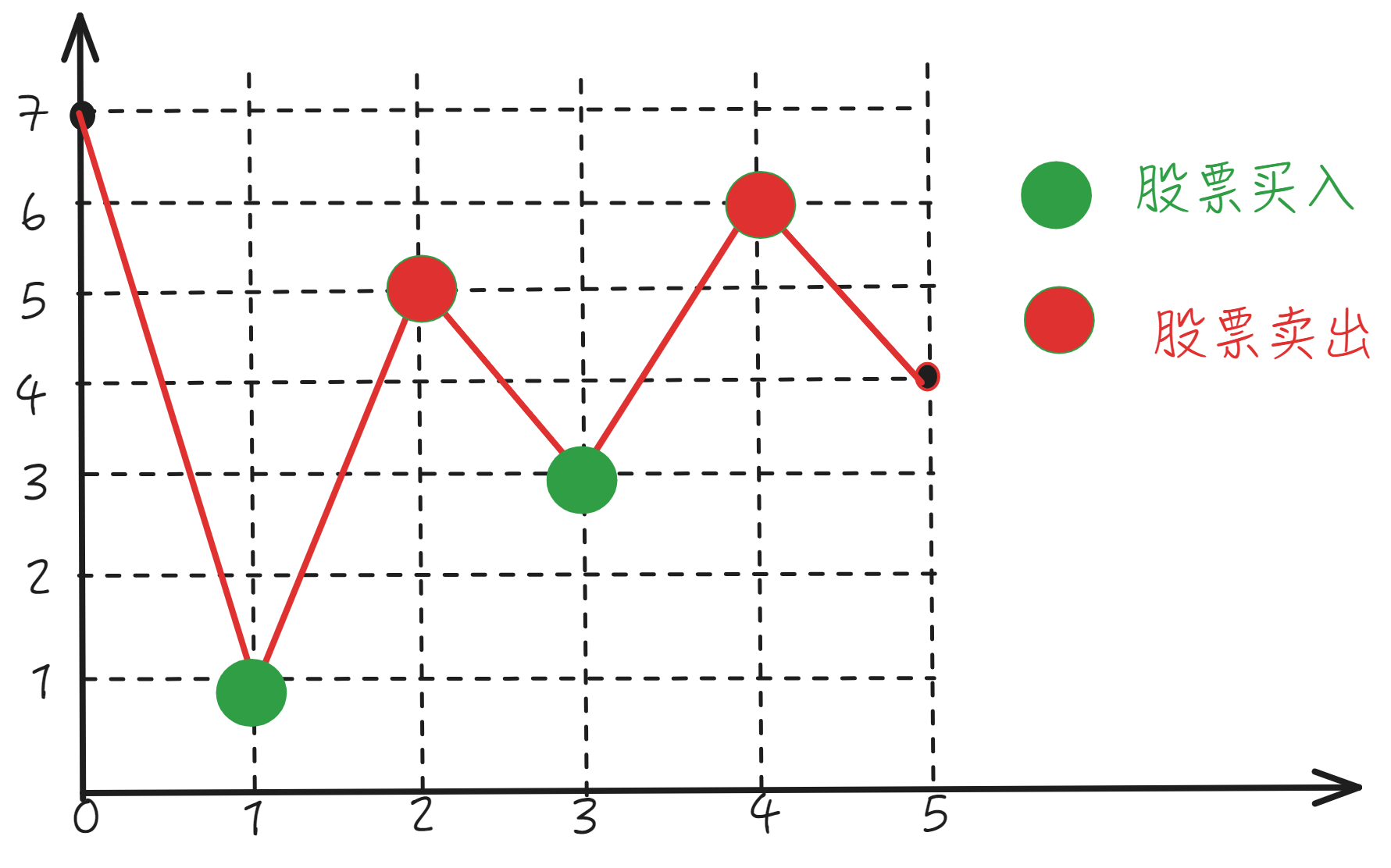
使用贪心算法解决。
从“贪心”(获取最大利润)角度考虑,如果当天卖出的价格高于前一天买入的价格就卖出,保证利润的最大化。
if(prices[i] > prices[i-1]){
profits += prices[i] - prices[i-1];
}
参考实现
class Solution {
public int maxProfit(int[] prices) {
int profit =0;
for (int i = 1; i < prices.length; i++) {
if(prices[i]>prices[i-1]){
profit+= prices[i] - prices[i-1];
}
}
return profit;
}
}
找零钱问题
问题描述
商店售货员找给 1 个顾客 n 元,用以下七种面值的纸币:100 元,50 元,20 元,10 元,5 元,2 元,1 元。
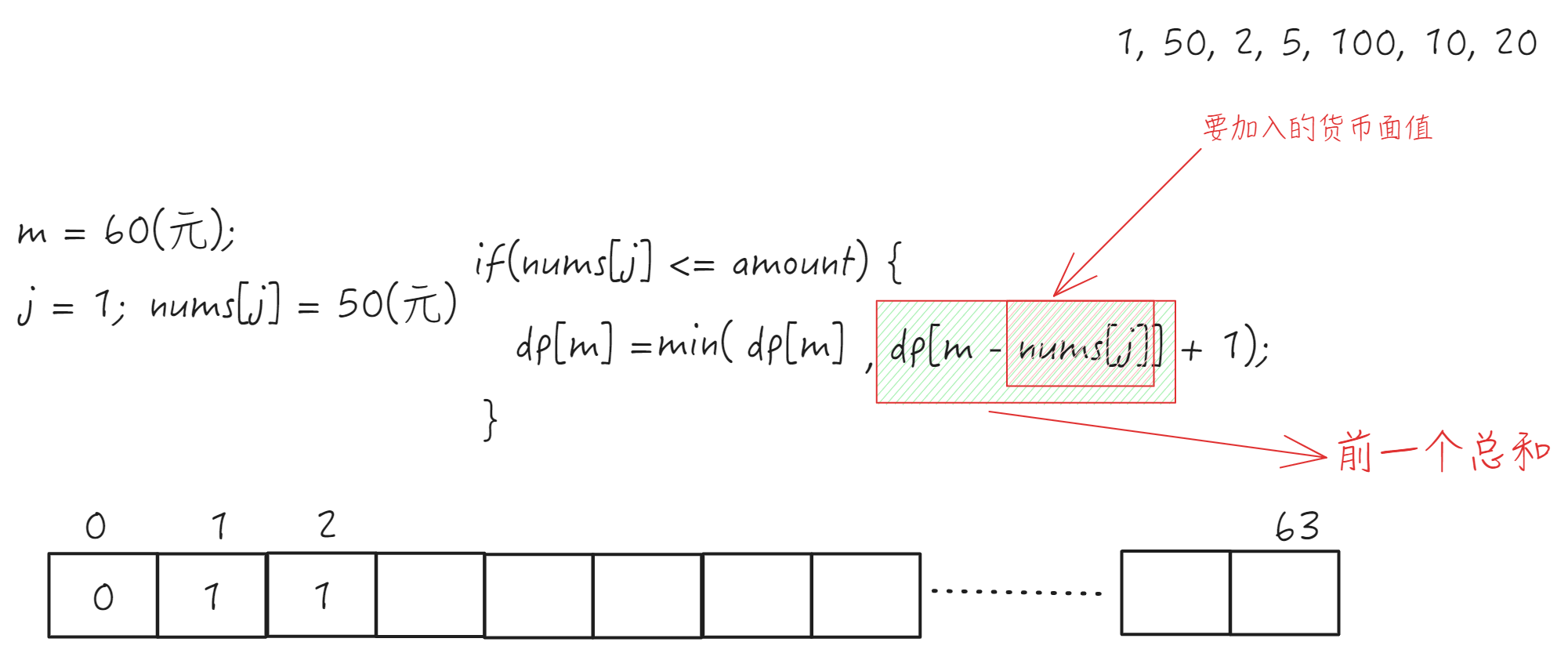
思考:如果商店售货员找给 1 个顾客 63元,假设钱币的面值有九种:100 元,50 元,20 元,10 元,5 元,2 元,1 元。用贪婪算法得到的是该问题的最优解吗?

动态规划(DP)
package com.ffyc.greedy;
import java.util.Arrays;
public class MoneyGreedyDp {
public int coinChange(int[] nums, int amount) {
int n = nums.length;
int[] dp = new int[amount+1];
for(int m = 1; m <=amount; m++){
dp[m] = amount+1;
for(int j =0; j<n;j++){
if(nums[j] <=m ){
dp[m] = Math.min(dp[m],dp[m-nums[j]]+1);
}
}
}
if(dp[amount] > amount){
return -1;
} else{
return dp[amount];
}
}
public static void main(String[] args) {
int[] nums = {1, 50, 2, 5, 100, 10, 20};
int mount = 63;
new MoneyGreedy().greedy(nums, mount);
}
}
贪心算法
先从货币值大的开始扫描,比如先选50,则剩余13元;再选择10元,则剩余3元。采用此策略直到扫描终止。
package com.ffyc.greedy;
import java.util.Arrays;
public class MoneyGreedy {
public void greedy(int[] nums, int amount) {
int n = nums.length;
//对零钱排序
Arrays.sort(nums);
int[] result = new int[n];
for (int i = n-1; i >=0; i--) {
if (amount >= nums[i]) {
result[i] = amount / nums[i];
amount = amount % nums[i];
}
}
if(amount > 0) {
System.out.println("剩余"+amount+"找零失败....");
return;
}
System.out.println(Arrays.toString(result));
}
public static void main(String[] args) {
int[] nums = {1, 50, 2, 5, 100, 10, 20};
int mount = 63;
new MoneyGreedy().greedy(nums, mount);
}
}
