优选算法合集————双指针(专题一)

题目一：移动零

题目描述：

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

示例 2:

输入: nums = [0]
输出: [0]

题目解析：

本题要求我们，在不移动数组的情况下，将数组内所有的0元素移动到末尾，且其他元素不能改变，我们可以创建两个指针，让一个指针去遍历数组，一个指针等待着交换，我们使用数组下标来代替指针。

算法思路：

1，让cur遍历数组，元素为0的时候，cur++;

2，当cur遇到非零的元素，dest++；并且与cur进行交换，cur++；

3，直到cur下标等于arr.length，循环结束。

代码实现：

class Solution {
    public void moveZeroes(int[] nums) {
        int cur = 0;
        int dest = -1;
        int tmp;
        while(cur<nums.length){
            if(nums[cur]==0){
                cur++;
            }else{
                dest++;
                tmp = nums[cur];
                nums[cur] = nums[dest];
                nums[dest] = tmp;
                cur++;
            }
        }
    }

}

题目二：覆写零

题目描述：

给你一个长度固定的整数数组 arr ，请你将该数组中出现的每个零都复写一遍，并将其余的元素向右平移。

注意：请不要在超过该数组长度的位置写入元素。请对输入的数组 就地 进行上述修改，不要从函数返回任何东西。

示例 1：

输入：arr = [1,0,2,3,0,4,5,0]
输出：[1,0,0,2,3,0,0,4]
解释：调用函数后，输入的数组将被修改为：[1,0,0,2,3,0,0,4]

示例 2：

输入：arr = [1,2,3]
输出：[1,2,3]
解释：调用函数后，输入的数组将被修改为：[1,2,3]

题目解析：

题目的意思就是我们遍例数组的时候，如果遇到0，我们就要打印两遍0，如果是其他的，打印一次，但不能超过数组原有的长度，我们还是定义两个指针。

算法思路：

1，定义指针dest，cur，先让cur,dest,模拟遍历一次数组，dest下标为arr,length时停止，记录下cur的位置，

2，如果开始dest在n下标，cur下标对应的数为0，让arr[n-1]=0，dest-=2，cur-=1;

3，从cur下标开始往前遍历，让dest重写我们的数组。

代码实现：

class Solution {
    public void duplicateZeros(int[] arr) {
        int dest = -1;
        int cur = 0;
        int s = arr.length;
        while(dest<s-1){
            if(arr[cur]==0){
                dest+=2;
            }
            else{
                dest++;
            }
            cur++;
        }
        cur--;
        if(dest==s){
            arr[s-1] = 0;
            dest-=2;
            cur--;
        }

        while(cur>=0){
            if(arr[cur]==0){
                arr[dest]=0;
                dest--;
                arr[dest]=0;
                dest--;
                cur--;
            }else{
                arr[dest]=arr[cur];
                dest--;
                cur--;
            }
        }
    }
}

题目三：快乐数

题目描述：

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

示例 1：

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

示例 2：

输入：n = 2
输出：false

题目解析：

题会给到一个整数，整数的每个位上的数可以拆开进行平方，如果这个数一直进行这个操作，直到得数为1时，它就是快乐数，这题我们该怎么写呢，大家有没有做过环形链表求入口点的，

我们可以把这道题想像成链表求交点，利用快慢指针，快指针变化两次，慢指针变化一次，这里的变化指的就是把数拆开求平方，直到相遇，看看相遇点是不是1，（我们所能填入的数是一定会相遇的，这里不讲原理了） 

算法思路：

快慢指针，求交点

 代码实现：

class Solution {
    public int change(int n){
        int num = 0;
        int a = 0;
        while(n!=0){
            a = n%10;
            num+=a*a;
            n/=10;
        }
        return num;
    }
    public boolean isHappy(int n) {
        int fast = change(n);
        int slow = n;
        while(fast!=slow){
            fast = change(change(fast));
            slow = change(slow);
        }
        if(fast==1){
            return true;
        }
        return false;
    }
}

题目四：盛水最多的容器

题目描述：

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

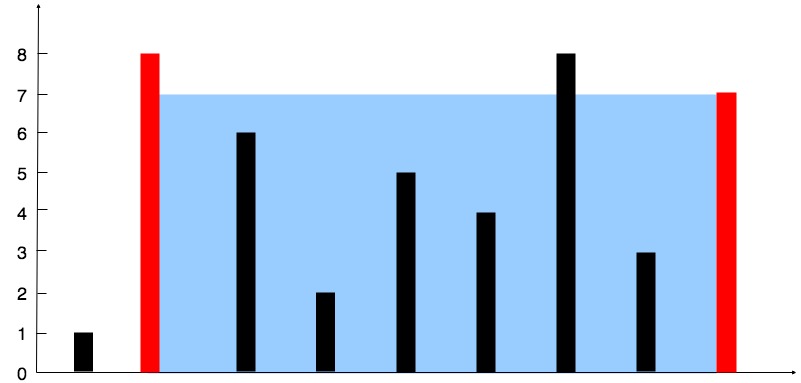
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

题目解析：

数组下标可以看作我们的长，数组下标的值可以当做高，并且高只计算最短边，让我们找到最大的容积，我们可以使用暴力枚举，不用想，绝对会超时，这时我们可以想想排序，单调性，二分等等，找这道题有没有规律。

因为高我们看的是小的高，先看cur，无论我们怎么选另一边的高，高也只能为1，所以我们这时只要关注长就行了。

算法思路：

1，cur与dest下标的值进行比较，小下标的h*（dest-cur）为每次的容积；小下标移动

2，直到cur==dest；

3，比较求出的最大值；

代码实现：

class Solution {
    public int maxArea(int[] height) {
        int cur = 0;
        int dest = height.length-1;
        int max = 0;
        while(cur<dest){
            if(height[cur]<=height[dest]){
                int a = 0;
                a = height[cur]*(dest-cur);
                if(a>=max) max = a;
                cur++;
            }else{
                int a = 0;
                a = height[dest]*(dest-cur);
                if(a>=max) max = a;
                dest--;
            }
        }
        return max;
    }
}

题目五：有效三角形的个数

题目描述：

给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

示例 1:

输入: nums = [2,2,3,4]
输出: 3
解释:有效的组合是: 
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3

示例 2:

输入: nums = [4,2,3,4]
输出: 4

提示:

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000

题目解析： 

我们在给的一组数据中挑选3个符合三角形构成规则的数，我们依旧可以使用暴力枚举，3层循环，不用想绝对超时，我们知道三角形是两边之和大于第三边，转化为编程条件就是a+b>c，b+c>a，a+c>b；这里我们可以使用一个小技巧，就是当a<b<c的时候，我们只需要判断a+b>c就行了，因为那两个条件在a<b<c时是一定成立的，我们可以尝试排序数组，再利用单调性解决问题。

算法思路： 

1，给数组排序，固定一个大数c

2，数组0下标a，c-1为b，利用单调性双指针判断a+b与c的关系

3，利用单调性移动a和b的下标。

代码实现：

class Solution {
    public int triangleNumber(int[] nums) {
        int c = nums.length-1;
        int a = 0;
        int b = c-1;
        int count = 0;
        Arrays.sort(nums);
        for(;c>=2;c--){
            a = 0; b = c-1;
            while(a<b){
                if(nums[a]+nums[b]>nums[c]){
                    count += (b-a);
                    b--;
                }else{
                    a++;
                }
            }
        }
        return count;
    }
}

题目六：和为s的两个数字

题目描述：

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target  的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

题目解析：

这到题是让我们在数组中找到一组数，让他俩的和为target，这到题之前是递增的数组，我们就可以使用双指针，单调性来做，但是现在改了，不有序了，我们只能使用哈希表来做了，大家当一个知识扩展吧。

 算法思路：

1，创建哈希表，遍历数组

2，查询数组中是否存在targert-nums[i]；如果存在返回下标

3，不存在将元素put到哈希表中。

代码实现： 

class Solution {
    public int[] twoSum(int[] nums, int target) {
        HashMap<Integer,Integer> hashMap = new HashMap<>();
        for(int i=0;i<nums.length;i++){
            if(hashMap.containsKey(target-nums[i])){
                return new int[]{hashMap.get(target-nums[i]),i};
            }
            hashMap.put(nums[i],i);
        }
        return new int[0];
    }
}

题目七：三数之和

题目描述：

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

题目解析： 

要在题目给的数组中挑出3个不重复的元素让他们相加为0，我们在找到所有元素后还要进行去重操作，我们可以使用暴力枚举也就是三层循环，绝对超时，我们使用了暴力枚举，想找规律，排序，单调性，双指针，二分等等办法，

算法思路： 

1，固定一个数a，让letf=a+1,right=arr.length-1；

2，利用单调性判断left和right的移动方向；

3，让a从头开始直到n-1；

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        int a = 0;
        int left = 0;
        int right = 0;
        int n = nums.length;
        Arrays.sort(nums);
        int target = 0;
        List<List<Integer>> list1 = new LinkedList<>();
        for(;a<n;){
            left = a+1; right = n-1; target = -nums[a];
            while(left<right){
                if(nums[left]+nums[right]<target){
                    left++;
                }else if(nums[left]+nums[right]>target){
                    right--;
                }else{
                    List<Integer> list2 = new LinkedList<>();
                    list2.add(nums[a]);
                    list2.add(nums[left]);
                    list2.add(nums[right]);
                    list1.add(list2);
                    left++;
                    right--;
                    while(left<right && nums[left]==nums[left-1]) left++;
                    while(left<right && nums[right]==nums[right+1]) right--;
                }
            }
            a++;
            while(a<n && nums[a]==nums[a-1]) a++;
        }
        return list1;
    }
}

 扩展题型：

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

• 0 <= a, b, c, d < n
• a、b、c 和 d 互不相同
• nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按 任意顺序 返回答案 。

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：

输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

思路是一样的；

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> list1 = new LinkedList<>();
        Arrays.sort(nums);
        int a = 0;
        int b = 0;
        int left = 0;
        int right = 0;
        int n = nums.length;
        long target2 = 0;
        for(;a<n;){
            b = a+1;
            target2 = (long)target-(long)nums[a]; 
            for(;b<n;){
                left = b+1; right = n-1;
                while(left<right){
                    if(nums[left]+nums[right]<target2-nums[b]){
                        left++;
                    }else if(nums[left]+nums[right]>target2-nums[b]){
                        right--;
                    }else{
                        List<Integer> list2 = new LinkedList<>();
                        list2.add(nums[a]);
                        list2.add(nums[b]);
                        list2.add(nums[left]);
                        list2.add(nums[right]);
                        list1.add(list2);
                        left++;
                        right--;
                        while(left<right && nums[left]==nums[left-1]) left++;
                        while(left<right && nums[right]==nums[right+1]) right--;
                    }
                }
                b++;
                while(b<n && nums[b]==nums[b-1]) b++;
            }
            a++;
            while(a<n && nums[a]==nums[a-1]) a++;
        }
        return list1;
    }
}