数学建模-----假设性检验引入+三个经典应用场景(三种不同的假设性检验类型)
文章目录
- 1.假设检验的过程
- 1.1问题的提出
- 1.2证据的引入
- 1.4做出结论
- 2.案例二:汽车引擎排放
- 2.1进行假设
- 2.2假设检验的类型
- 2.3抽样分布的类型
- 2.4单尾(双尾)检验
- 2.5t检验
- 3.案例三:特鲁普效应
- 3.1统计显著和效果显著
- 3.2心理学现象
- 3.3进行假设检验
- 4.案例四:AB测试
- 4.2进行假设
- 4.3计算样本概率的平均值
- 4.4和显著水平进行比较
- 5.我的总结
之前一直遇到这个假设检验,但是一直不理解这个假设性检验的过程,今天在这个知乎上面看到了一个文章,感觉这个里面的案例把这个假设性检验的过程描述的很详细,分享一下;
假设性检验生动讲解
下面我也是使用这个文章里面的案例加上自己的这个理解总结复盘一下;
1.假设检验的过程
1.1问题的提出
下面的这个案例里面的任务我确实不是很熟悉,但是这个案例确实很容易让我们理解这个假设性检验的过程;
首先就是建立这个问题的两个假设:
1)零假设:2)备选假设;
这两个假设,其实是有关系的,如果一个不成立,另外一个肯定是成立的,这两个假设在这个逻辑上面是互补的,如果我们可以证明其中的一个,另外一个肯定是成立的;

1.2证据的引入
合理足够多的样本可以代表这个整体;
在零假设成立的情况下,这个马蓉没有出轨的概率是0.01%;
 ## 1.3判断标准
## 1.3判断标准
我们的这个样本的这个统计的数据结果概率:0.01%(马蓉没有出轨);
我们的判断的标准就是马蓉出轨的这个概率小于5%,我们证明这个零假设成立,但是这个里面的0.01%显然是小于这个5%的,这个5%在我们的这个统计学里面是属于这个p值(显著性水平,在我们的这个概率里面,这个p值是可进行选择的,一般就是1%,5%之类的,我们下面的这个案例里面使用的就是5%,我们的这个概率就是和这个显著性水平进行比较的),他是有自己的这个名字的;
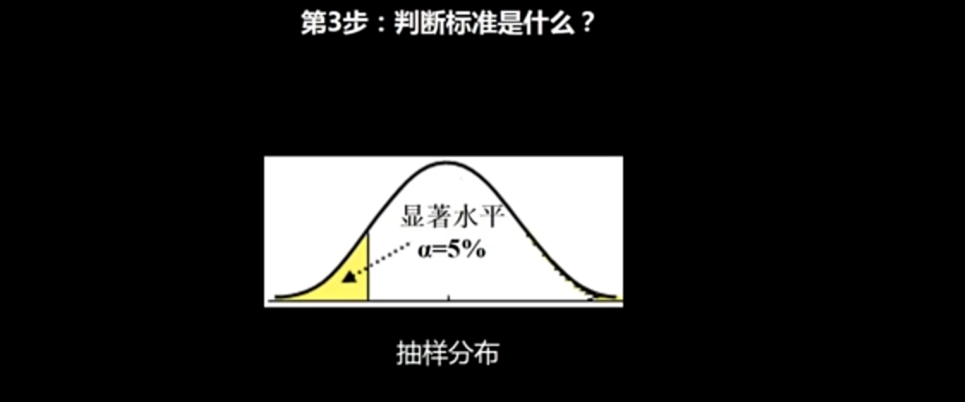
1.4做出结论
概率《《p值,我们就可以证明这个零假设不成立,也就是这个时候我们可以拒绝这个零假设,因此我们的这个备选假设是成立的,因此这个推理的结果就是马蓉出轨了(备选假设);
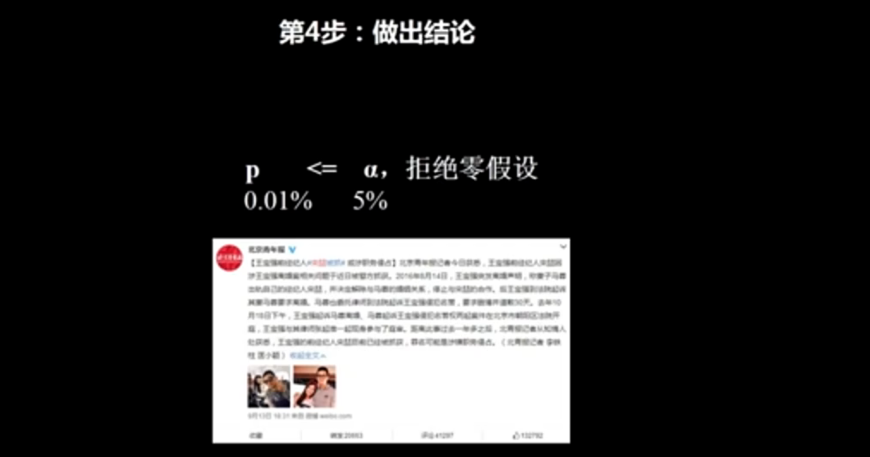
2.案例二:汽车引擎排放
排放标准是这个排放平均值:<20ppm,我们已知这个相关的统计数据;
2.1进行假设
还是和上面的一样,我们进行这个零假设和备选假设:根据这个引擎的排放量的大小进行区分;

2.2假设检验的类型
| 假设检验的类型 | 目的和过程 | 具体的案例 |
|---|---|---|
| 单样本检验 | 检验单个样本的平均值是不是等于目标数值 | 某一个大学里面的这个学生的平均身高是不是大于全国的平均身高 |
| 相关样本配对检验 | 检验相关的样本的或者是配对的样本,看看这个平均值是不是等于平均值 | 检验一个群体服用减肥药前后的这个体重的变化(缺点就是有残留效应) |
| 独立双样本检验 | 检验两个样本的平均值是否等于目标数值 | 检验闯关游戏的教学方法是不是有效,在这个课堂上面进行测试(因为是独立检验,因此需要大量数据) |
2.3抽样分布的类型
我们可以使用这个相关的内置函数(python或者是matlab)把我们的这个数据集丢进去,让这个内置函数进行判断我们的这个数据集是不是符合t分布;
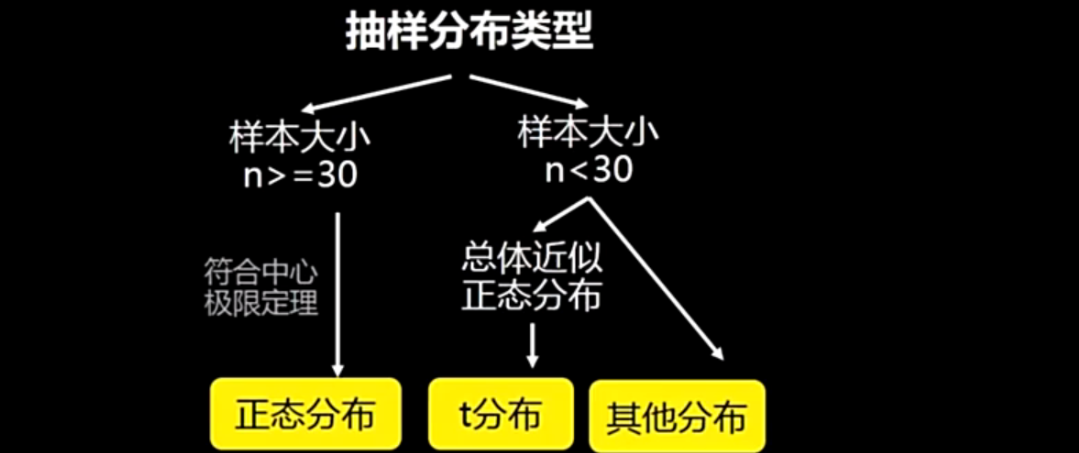
2.4单尾(双尾)检验
公式汽车引擎的排放标准就是<20,因此这个案例就是属于左尾检验
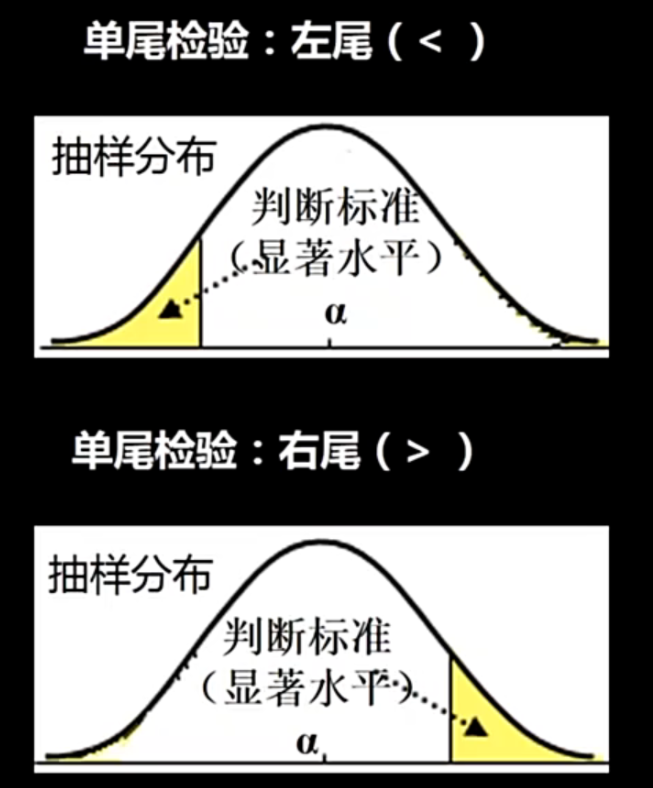
如果我们的这个假设属于是不等于某一个数值,而不是单纯的大于或者是小于,这个不等于就会要求我们考虑这个左右区间,这个时候就是双尾检验(这个时候两边的这个显著性水平都需要被判断);
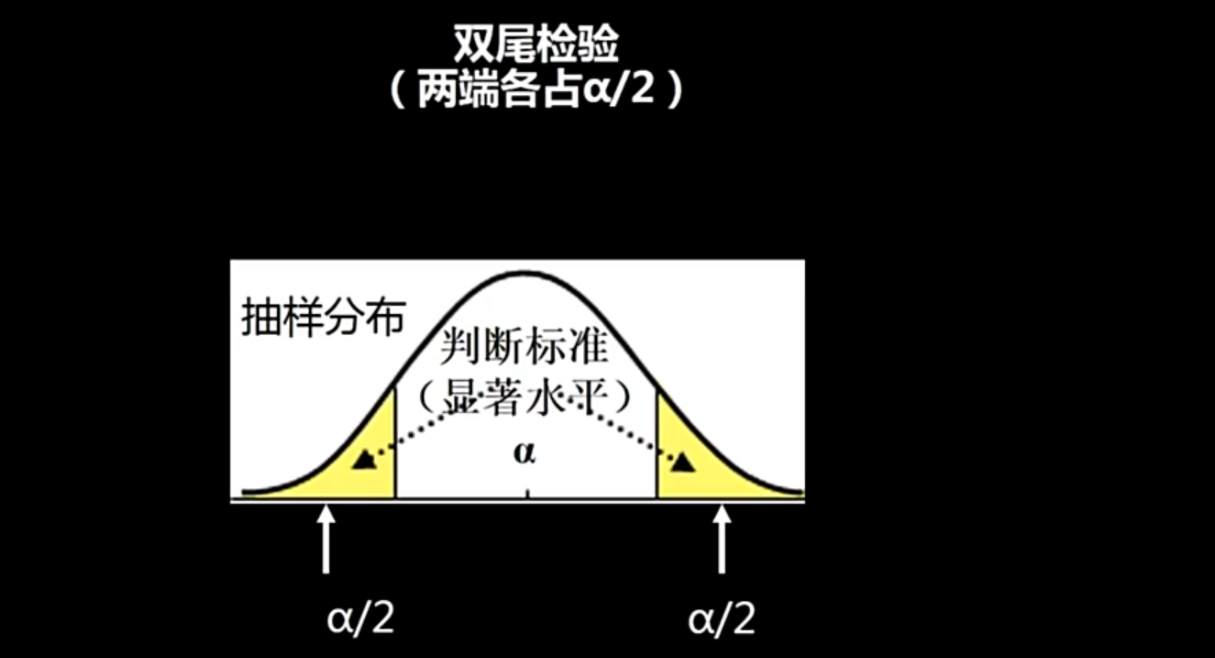
我们很多的计算软件或者是工具计算出来的这个都是双尾的p值,单尾和双尾之间的关系就是我们使用这个双尾的计算结果除以2就是单尾的;
2.5t检验
戈斯特:学生t检验–这个就是我们的t检验的由来,就是这个员工不允许发文章,他就以一个笔名叫作“学生“的账号偷偷发文章,后来变得很出名,这个t检验就是他搞出来的,他的名字就是上面说的这个戈斯特,于是为了纪念,这个检验就叫做学生t检验,后来我们简单的说成是t检验
假设汽车引擎排放标准满足我们的零假设,这个时候的样本数据的平均值的概率是0.0074,即0.74%;
上面的这个汽车的引擎排放标准就是属于单样本的单尾检验的范畴,单样本就是我们的这个数据之间的关系,都是相同的属性,单尾就是我们的这个平均值是不是<20判断的这个情况;
3.案例三:特鲁普效应
3.1统计显著和效果显著
假设检验:统计显著(是不是有差异);
效应量:存在差异的时候,这个差异的大小;
3.2心理学现象
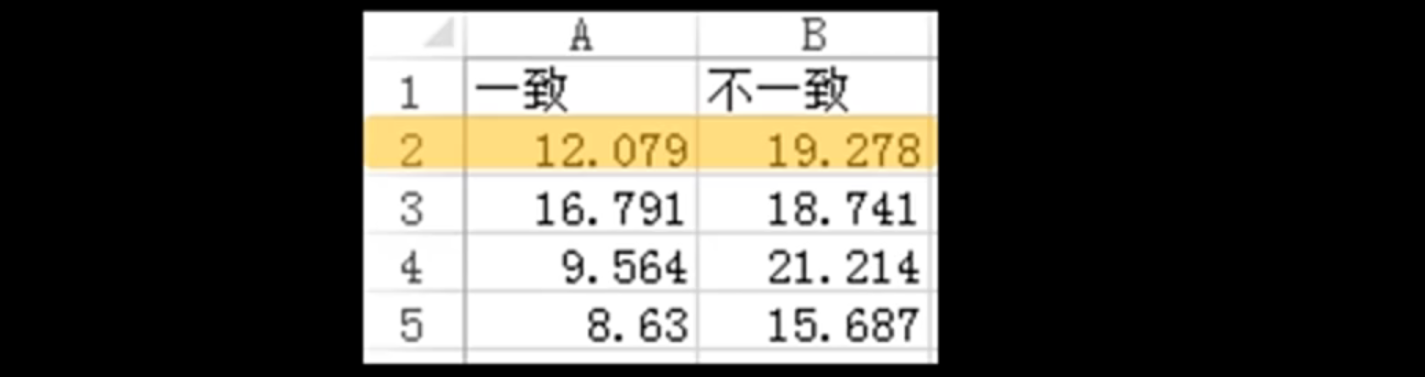
就是我们的两组数据:
1)第一组这个字体内容和颜色一致,我们进行朗读;
2)第二组的这个颜色和内容不一致,我们进行朗读;

下面的这个就是我们的分析结果:可以说明一些问题,即我们记住第二组需要花费更长的时间;
3.3进行假设检验

因为第一组和第二组都是相同人员,因此这个案例就是相关配对检验;
因为这个是特鲁普效应存在,就是第一次的这个测试数据小于第二组的,因此这个使用的就是单尾检验里面的这个左尾检验;
我们计算这个获取样本数据平均值的概率和我们的这个显著性水平进行比较,就是和0.05进行比较,因为是小于0.05,所以这个原假设是不成立的,证明这个效应存在的;
4.案例四:AB测试
给出来两个版本,看看哪一个的效果会更加好;
依据:相同时间打错字的数量;就是我们抽调两组人,一组测试这个A版本,一组测试这个B版本,这个时候查看他们的这个打错字的数量,使用这个平均值衡量我们的两版本之间的这个差异是不是存在;

4.2进行假设
零假设:两个版本之间是没有差别的,就是打错字的这个平均值是一样的;
备选假设:两个版本的这个差别是存在的,两个的这个平均值不一样;

4.3计算样本概率的平均值
独立双样本t检验,而且是双尾检验(因为这个备选假设里面是我们的两个版本的这个平均值是不一样的,出现了这个不等号,符合我们上面说过的这个双尾检验的这个情况);

4.4和显著水平进行比较
上面的这个置信区间,就是我们的这个1-显著水平,也就是1-5%,但是由于这个是双尾检验,因此这个计算结果是和我们的2.5%进行比较的;
效应量就是两者存在差异的情况下,通过这个效应量计算这个差异的大小,衡量我们的这个存在差异的一个程度;
5.我的总结
1)我之前学习这个机器学习的时候就说过,一个好的案例是可以加深我们对于这个理论知识的理解的,今天这三个案例我认为就是好的案例;
2)上面介绍的三个案例分属于不同的类型和检验方法,覆盖的范围比较广,我认为是很适合初学者进行学习的;
3)汽车引擎排放标准就是一个单尾检验的情况,使用的方法就是我们的单样本的检验方法,也就是计算我们的这组数据的平均值即可;
4)特鲁普这个是心理学的现象,证明的是两个方式之间的这个平均值差异,而且是第一组小于第二组,使用的就是单尾检验,使用的就是我们的相关样本的配对检验;
5)AB测试就是两组键盘的这个格式进行测试,看看这个打错字的情况,我们的这个假设就是两个情况之下这个平均值是不是一样的,因此这个是独立双样本检验(因为使用两个版本的不是一组人);
6)通过上面的三个案例,我们了解了这个单样本检验,双样本配对检验,以及这个独立双样本检验,知道了这个单尾,双尾,以及两只之间的这个转换关系,这个也算是解决了我当前的疑惑,因为用过spaa的小伙伴就知道,这个spss进行分析的时候,就出现最后一栏表示的就是我们的这个双尾(之前一直不知道这个是什么,今天总算知道了);
7)即使到这里,这个并不是完结了,因此这个具体的计算我没有实操(由于一些原因),而且自己对于这个置信区间理解的不是很明细,后续会找案例看看这个具体的计算过程以及这个效应量,置信区间的具体含义等等,这个主要就是一个了解和入门,一切只是刚刚开始;
示的就是我们的这个双尾(之前一直不知道这个是什么,今天总算知道了);
7)即使到这里,这个并不是完结了,因此这个具体的计算我没有实操(由于一些原因),而且自己对于这个置信区间理解的不是很明细,后续会找案例看看这个具体的计算过程以及这个效应量,置信区间的具体含义等等,这个主要就是一个了解和入门,一切只是刚刚开始;
8)其实这个文章从昨天就开始写了,但是已知想要加深理解,所以今天又学了第二遍,之前也学过这个假设性检验的一些教程,但是都没有理解到现在的这个程度,这个也让我意识到了:一些知识的学习需要一个渐进的过程,这两天学明白了,并不代表之间的这个学习都是没用的,(就如同三个馒头的理论是一样的,吃第三个馒头吃饱了并不代表前面的两个没有用~~),这个也告诉我自己既不要在一个阶段停留太长时间(可能是因为当时我们的这个知识储备和各方面没有到位),但是我们在适当的时候对于之前的内容二次学习就会有新的理解和体会,这个就是我这两天学习这个假设性检验的一个心得体会~
