深度学习在推荐系统中的应用

参考自《深度学习推荐系统》，用于学习和记录。

前言

（1）与传统的机器学习模型相比，深度学习模型的表达能力更强，能够挖掘（2）深度学习的模型结构非常灵活，能够根据业务场景和数据特点，灵活调整模型结构，使模型与应用场景完美契合。

主流深度学习推荐模型的演化图谱

AutoRec 单隐层神经网络推荐模型

AutoRec 将自编码器（AutoEncoder）的思想和协同过滤结合，提出了一种单隐层神经网络推荐模型。

AutoRec模型是一个标准的自编码器，它的基本原理是利用协同过滤中的共现矩阵，完成物品向量或者用户向量的自编码。再利用自编码的结果得到用户对物品的预估评分，进而进行推荐排序。

自编码器

自编码器是指能够完成数据“自编码”的模型。无论是图像、音频，还是数据，都可以转换成向量的形式进行表达。假设其数据向量为 $r$ 自编码器的作用是将向量 $r$ 作为输入，通过自编码器后，得到的输出向量尽量接近其本身。

假设自编码器的重建函数为 $h(r;\theta )$ ，那么自编码器的目标函数为

$$\underset{\theta }{\min }\sum _{r\in S}\Vert r-h(r;\theta ){\Vert }_2^2$$

其中， $s$ 是所有数据向量的集合。

在完成自编码器的训练后，就相当于在重建函数 $h(r;\theta )$ 中存储了所有数据向量的“精华”。一般来说，重建函数的参数数量远小于输人向量的维度数量，因此自编码器相当于完成了数据压缩和降维的工作。

对一个物品i来说，所有 $m$ 个用户对它的评分可形成一个 $m$ 维的向量 $r^{(i)}=(R_{1i},\dots ,R_{mi})$ ，AutoRec 要解决的问题是构建一个重建函数 $h(r;\theta )$ ，使所有该重建函数生成的评分向量与原评分向量的平方残差和最小。在得到 AutoRec 模型的重建函数后，还要经过评分预估和排序的过程才能得到最终的推荐列表。

下面为 AutoRec 模型的两个重点内容一重建函数的模型结构和利用重建函数得到最终推荐列表的过程。

AutoRec 模型的结构

网络的输入层是物品的评分向量 $r$ ，输出层是一个多分类层。图中蓝色的神经元代表模型的 $k$ 维单隐层，其中 $k<<m$

图中的 $V$ 和 $W$ 分别代表输入层到隐层，以及隐层到输出层的参数矩阵。该模型结构代表的重建函数的具体形式如下所示。
$$h(r;\theta )=f(W\cdot g(Vr+\mu )+b)$$

其中， $f(\cdot ),g(\cdot )$ 分别为输出层神经元和隐层神经元的激活函数。

为防止重构函数的过拟合，在加人L2正则化项后，AutoRec目标函数的具体形式如下所示。

$$\underset{\theta }{\min }\sum _{i=1}^n\Vert {\mathbf{r}}^{(i)}-\mathbf{h}({\mathbf{r}}^{(i)};\theta ){\Vert }_{\mathcal{O}}^2+\frac{\lambda }{2}\cdot (\Vert \mathbf{W}{\Vert }_F^2+\Vert \mathbf{V}{\Vert }_F^2)$$

由于 AutoRec 模型是一个非常标准的三层神经网络，模型的训练利用梯度反向传播即可完成。

神经元、神经网络和梯度反向传播

• 单神经元模型结构
  
• 简单神经网络
  

利用求导过程中的链式法则（ChainRule），可以解决梯度反向传播的问题。最终的损失函数到权重 $w_1$ 的梯度是由损失函数到神经元 $h_1$ 输出的偏导，以及神经元 $h_1$ 输出到权重 $w_1$ 的偏导相乘而来的。也就是说，最终的梯度逐层传导回来，“指导”权重 $w_1$ 的更新。

$$\frac{\partial L_{o_1}}{\partial w_1}=\frac{\partial L_{o_1}}{\partial h_1}\cdot \frac{\partial h_1}{\partial w_1}$$

在具体的计算中，需要明确最终损失函数的形式，以及每层神经元激活函数的形式，再根据具体的函数形式进行偏导的计算。

基于 AutoRec 模型的推荐过程

基于AutoRec模型的推荐过程并不复杂。当输入物品i的评分向量为 $r^{(\mathrm{i})}$ 时，模型的输出向量 $h(r^{(\mathbf{i})};\theta )$ 就是所有用户对物品i的评分预测。那么，其中的第 $u$ 维就是用户 $\mathbf{u}$ 对物品i的预测 ${\hat{R}}_{\mathrm{mi}}$ ，如下所示。

$${\hat{R}}_{\mathbf{ui}}=\left(h\right(r^{(\mathbf{i})};\hat{\theta }){)}_u$$

通过遍历输入物品向量就可以得到用户u对所有物品的评分预测，进而根据评分预测排序得到推荐列表。

与之前的协同过滤算法一样，AutoRec也分为基于物品的AutoRec和基于用户的AutoRec。以上介绍的AutoRec输入向量是物品的评分向量，因此可称为I-AutoRec（ItembasedAutoRec），如果换做把用户的评分向量作为输入向量，则得到U-AutoRec（User based Auto Rec）。

AutoRec 特点和局限性

AutoRec模型从神经网络的角度出发，使用一个单隐层的AutoEncoder泛化用户或物品评分，使模型具有一定的泛化和表达能力。由于AutoRec模型的结构比较简单，使其存在一定的表达能力不足的问题。

在模型结构上，AutoRec模型和后来的词向量模型（Word2vec）完全一致，但优化目标和训练方法有所不同。

Deep Crossing 模型——经典的深度学习架构

相比 AutoRec 模型过于简单的网络结构带来的一些表达能力不强的问题， DeepCrossing 模型完整地解决了从特征工程、稀疏向量稠密化、多层神经网络进行优化目标拟合等一系列深度学习在推荐系统中的应用问题，为后续的研究打下了良好的基础。

Deep Crossing

DeepCrossing模型的应用场景是微软搜索引擎Bing中的搜索广告推荐场景。

针对该使用场景，微软使用的特征如表3-1所示，这些特征可以分为三类：一类是可以被处理成 one-hot 或者 multi-hot 向量的类别型特征，包括用户搜索词（query）、广告关键词（keyword）、广告标题（title）、落地页（landing page）、匹配类型（matchtype）；一类是数值型特征，微软称其为计数型（counting）特征，包括点击率、预估点击率（clickprediction）；一类是需要进一步处理的特征，包括广告计划（campaign）、曝光样例（impression）、点击样例（click）等。严格地说，这些都不是独立的特征，而是一个特征的组别，需要进一步处理。例如，可以将广告计划中的预算（budget）作为数值型特征，而广告计划的id则可以作为类别型特征。

类别型特征可以通过 one-hot 或 multi-hot 编码生成特征向量，数值型特征则可以直接拼接进特征向量中，在生成所有输人特征的向量表达后， DeepCrossing 模型利用该特征向量进行CTR预估。

Deep Crossing 模型的网络结构

为完成端到端的训练，DeepCrossing模型要在其内部网络中解决如下问题。

（1）离散类特征编码后过于稀疏，不利于直接输人神经网络进行训练，如何解决稀疏特征向量稠密化的问题。

（2）如何解决特征自动交叉组合的问题。（3）如何在输出层中达成问题设定的优化目标。

DeepCrossing模型分别设置了不同的神经网络层来解决上述问题。如图所示，4层—Embedding层、Stacking层、Multiple ResidualUnits层和Scoring层。接下来，从下至上依次介绍各层的功能和实现。

Embedding层：Embedding层的作用是将稀疏的类别型特征转换成稠密的Embedding向量。

Stacking层：Stacking层（堆叠层）的作用比较简单，Embedding特征和数值型特征拼接在一起，形成新的包含全部特征的特征向量，该层通常也被称为连接（concatenate）层。

MultipleResidualUnits层：该层的主要结构是多层感知机，相比标准的以感知机为基本单元的神经网络，DeepCrossing模型采用了多层残差网络（Multi-Layer Residual Network）作为MLP的具体实现。通过多层残差网络对特征向量各个维度进行充分的交叉组合，使模型能够抓取到更多的非线性特征和组合特征的信息，进而使深度学习模型在表达能力上较 传统机器学习模型大为增强。

什么是残差神经网络，其特点是什么

• 残差单元
  

与传统的感知机不同，残差单元的特点主要有两个：

（1）输入经过两层以ReLU为激活函数的全连接层后，生成输出向量。

（2）输入可以通过一个短路（shortcut）通路直接与输出向量进行元素加（element-wiseplus）操作，生成最终的输出向量。

在这样的结构下，残差单元中的两层ReLU网络其实拟合的是输出和输人之间的“残差” $x^{\mathrm{o}}-x^{\mathrm{i}}$ ），这就是残差神经网络名称的由来。

残差神经网络的诞生主要是为了解决两个问题：

（1）神经网络是不是越深越好？对于传统的基于感知机的神经网络，当网络加深之后，往往存在过拟合现象，即网络越深，在测试集上的表现越差。而在残差神经网络中，由于有输入向量短路的存在，很多时候可以越过两层ReLU网络，减少过拟合现象的发生。

（2）当神经网络足够深时，往往存在严重的梯度消失现象。梯度消失现象是指在梯度反向传播过程中，越靠近输人端，梯度的幅度越小，参数收敛的速度越慢。为了解决这个问题，残差单元使用了ReLU激活函数取代原来的sigmoid激活函数。此外，输人向量短路相当于直接把梯度毫无变化地传递到下一层，这也使残差网络的收敛速度更快。

Scoring层：Scoring层作为输出层，就是为了拟合优化目标而存在的。对于CTR预估这类二分类问题（点击广告或内容的概率），Scoring层往往使用的是逻辑回归模型，而对于图像分类等多分类问题，Scoring层往往采用softmax模型。

NeuralCF 模型——CF 与深度学习的结合

如果从深度学习的视角看待矩阵分解模型，那么矩阵分解层的用户隐向量和物品隐向量完全可以看作一种Embedding方法。最终的“Scoring层”就是将用户隐向量和物品隐向量进行内积操作后得到“相似度”，这里的“相似度”就是对评分的预测。综上，利用深度学习网络图的方式来描述矩阵分解模型的架构：

在实际使用矩阵分解来训练和评估模型的过程中，往往会发现模型容易处于欠拟合的状态，究其原因是因为矩阵分解的模型结构相对比较简单，特别是“输出层”（也被称为“Scoring层”），无法对优化目标进行有效的拟合。这就要求模型有更强的表达能力，在此动机的启发下，新加坡国立大学的研究人员提出了NeuralCF模型。

NeuralCF

如图所示，NeuralCF用“多层神经网络 $+$ 输出层的结构替代了矩阵分解模型中简单的内积操作。这样做的收益是直观的，一是让用户向量和物品向量做更充分的交叉，得到更多有价值的特征组合信息；二是引人更多的非线性特征，让模型的表达能力更强。

原始的矩阵分解使用“内积”的方式让用户和物品向量进行交互，为了进一步让向量在各维度上进行充分交叉，可以通过“元素积”（element-wiseproduct，长度相同的两个向量的对应维相乘得到另一向量）的方式进行互操作，再通过逻辑回归等输出层拟合最终预测目标。

softmax 函数

给定一个 ${}_n$ 维向量，softmax函数将其映射为一个概率分布。标准的softmax函数 $\sigma :{\mathbb{R}}^n\to {\mathbb{R}}^n$ 由下面的公式定义：

$$\sigma (X{)}_i=\frac{\exp (x_i)}{{\sum }_{j=1}^n\exp \left(x_j\right)}$$
可以看到，softmax函数解决了从一个原始的 $n$ 维向量，向一个 $n$ 维的概率分布映射的问题。

在分类问题中，softmax函数往往和交叉熵（cross-entropy）损失函数一起使用：

$${\mathrm{Loss}}_{\mathrm{Cross}\mathrm{Entriopy}}=-\sum _i{y}_i\ln (\sigma (x{)}_i)$$

其中， $y_i$ 是第 $i$ 个分类的真实标签值， $\sigma (x{)}_i$ soft max $i$ 个分类的预测值。因为softmax函数把分类输出标准化成了多个分类的概率分布，而交叉熵正好刻画了预测分类和真实结果之间的相似度，所以softmax函数往 往与交叉熵搭配使用。在采用交叉熵作为损失函数时，整个输出层的梯度下降形式变得异常简单。

softmax函数的导数形式为

$$\frac{\partial \sigma (x{)}_i}{\partial x_j}=\{\begin{array}{l}\sigma (x{)}_i(1-\sigma (x{)}_j),i=j\\ -\sigma (x{)}_i\cdot \sigma (x{)}_j,i\ne j\end{array}$$

基于链式法则，交叉熵函数到softmax函数第 $j$ 维输人 $x_j$ 的导数形式为

$$\frac{\partial \mathrm{Loss}}{\partial x_j}=\frac{\partial \mathrm{Loss}}{\partial \sigma (x)}\cdot \frac{\partial \sigma (x)}{\partial x_j}$$
在多分类问题中，真实值中只有一个维度是1，其余维度都为0。假设第 $k$ 维是1，即 $y_k=1$ ，那么交叉熵损失函数可以简化成如下形式：

$${\mathrm{Loss}}_{\mathrm{Croff}}=-\sum _i{y}_i\ln (\sigma (x{)}_i)=-y_k\cdot \ln (\sigma (x{)}_k)=-\ln (\sigma (x{)}_k)$$

则有

$$\frac{\partial \mathrm{Loss}}{\partial x_j}=\frac{\partial (-\ln (\sigma (x{)}_k))}{\partial \sigma (x{)}_k}\cdot \frac{\partial \sigma (x{)}_k}{\partial x_j}=-\frac{1}{\sigma (x{)}_k}\cdot \frac{\partial \sigma (x{)}_k}{\partial x_j}=\{\begin{array}{l}\sigma (x{)}_j-1,j=k\\ \sigma (x{)}_j,j\ne k\end{array}$$

可以看出，softmax函数和交叉熵的配合，不仅在数学含义上完美统一，而且在梯度形式上也非常简洁。基于上式的梯度形式，通过梯度反向传播的方法，即可完成整个神经网络权重的更新。

NeuralCF 模型的优势和局限性

NeuralCF模型实际上提出了一个模型框架，它基于用户向量和物品向量这两个Embedding层，利用不同的互操作层进行特征的交叉组合，并且可以灵活地进行不同互操作层的拼接。

NeuralCF模型也存在局限性。由于是基于协同过滤的思想进行构造的，所以NeuralCF模型并没有引入更多其他类型的特征，这在实际应用中无疑浪费了其他有价值的信息。

PNN 模型——加强特征交叉能力

NeuralCF模型的主要思想是利用多层神经网络替代经典协同过滤的点积操作，加强模型的表达能力。广义上，任何向量之间的交互计算方式都可以用来替代协同过滤的内积操作，相应的模型可称为广义的矩阵分解模型。

PNN 模型的网络架构

PNN模型的提出同样是为了解决CTR预估和推荐系统的问题。

相比Deep Crossing，PNN模型在输人、Embedding层、多层神经网络，以及最终的输出层部分并没有结构上的不同，唯一的区别在于PNN模型用乘积层（Product Layer）Deep Crossing Stacking。也就是说，不同特征的Embedding向量不再是简单的拼接，而是用Product操作进行两两交互，更有针对性地获取特征之间的交叉信息。

Product 层的多种特征交叉方式

PNN模型对于深度学习结构的创新主要在于乘积层的引入。具体地说，PNN模型的乘积层由线性操作部分（乘积层的z部分，对各特征向量进行线性拼接）和乘积操作部分（中乘积层的p部分）组成。其中，乘积特征交叉部分又分为内积操作和外积操作。

内积操作就是经典的向量内积运算，假设输入特征向量分别为 $f_i,f_j$ ，特征的内积互操作 $g_{\mathrm{inner}}\left(f_i,f_j\right)$ 的定义如下所示。

$$g_{\mathsf{inner}}(f_i,f_j)=⟨f_i,f_j⟩$$

外积操作是对输入特征向量 $f_i,f_j$ 的各维度进行两两交叉，生成特征交叉矩阵，外积互操作 $g_{\mathrm{outer}}(f_i,f_j)$ 的定义如下所示。

$$g_{\mathrm{outer}}(f_i,f_j)=f_i{f}_j^{\mathrm{T}}$$

外积互操作生成的是特征向量 $f_i,f_j$ 各维度两两交叉而成的一个 $M\times M$ 的方形矩阵（其中 $M$ 是输入向量的维度）。这样的外积操作无疑会直接将问题的复杂度从原来的 $M$ 提升到 $M^2$ ，为了在一定程度上减小模型训练的负担，PNN模型的论文中介绍了一种降维的方法，就是把所有两两特征Embedding向量外积互操作的结果叠加（Superposition），形成一个叠加外积互操作矩阵 $p$ ，具体定义如下所示。

$$p=\sum _{i=1}^N\sum _{j=1}^N{g}_{\mathrm{outer}}(f_i,f_j)=\sum _{i=1}^N\sum _{j=1}^N{f}_i{f}_j^{\mathrm{T}}=f_{\Sigma }{f}_{\Sigma }^{\mathrm{T}},f_{\Sigma }=\sum _{i=1}^N{f}_i$$

从最终形式看，叠加矩阵 $p$ 的最终形式类似于让所有特征Embedding向量通过一个平均池化层（AveragePooling）后，再进行外积互操作。

在实际应用中，还应对平均池化的操作谨慎对待。因为把不同特征对应维度进行平均，实际上是假设不同特征的对应维度有类似的含义。

PNN 模型的优势和局限性

PNN的结构特点在于强调了特征Embedding向量之间的交叉方式是多样化的，相比于简单的交由全连接层进行无差别化的处理，PNN模型定义的内积和外积操作显然更有针对性地强调了不同特征之间的交互，从而让模型更容易捕获特征的交叉信息。

但PNN模型同样存在着一些局限性，例如在外积操作的实际应用中，为了优化训练效率进行了大量的简化操作。此外，对所有特征进行无差别的交叉，在一定程度上忽略了原始特征向量中包含的有价值信息。

Wide&Deep 模型——记忆能力和泛化能力的综合

本节介绍的是自提出以来就在业界发挥着巨大影响力的模型一谷歌于2016年提出的Wide&Deep模型。Wide&Deep模型的主要思路正如其名，是由单层的Wide部分和多层的Deep部分组成的混合模型。其中，Wide部分的主要作用是让模型具有较强的“记忆能力”（memorization）；Deep部分的主要作用是让模型具有“泛化能力”（generalization），正是这样的结构特点，使模型兼具了逻辑回归和深度神经网络的优点一能够快速处理并记忆大量历史行为特征，并且具有强大的表达能力，不仅在当时迅速成为业界争相应用的主流模型，而且衍生出了大量以Wide&Deep模型为基础结构的混合模型，影响力一直延续到至今。

模型的记忆能力和泛化能力

“记忆能力”可以被理解为模型直接学习并利用历史数据中物品或者特征的“共现频率”的能力。一般来说，协同过滤、逻辑回归等简单模型有较强的“记忆能力”。由于这类模型的结构简单，原始数据往往可以直接影响推荐结果，产生类似于“如果点击过A，就推荐B”这类规则式的推荐，这就相当于模型直接记住了历史数据的分布特点，并利用这些记忆进行推荐。

对“强特征”的记忆：如果以“最终是否安装pandora”为数据标签（label），则可以轻而易举地统计出netflix&pandora这个特征和安装pandora这个标签之间的共现频率。假设二者的共现频率高达 $10\%$ （全局的平均应用安装率为 $1\%$ ），这个特征如此之强，以至于在设计模型时，希望模型一发现有这个特征，就推荐pandora这款应用（就像一个深刻的记忆点一样印在脑海里），这就是所谓的模型的“记忆能力”。像逻辑回归这类简单模型，如果发现这样的“强特征”，则其相应的权重就会在模型训练过程中被调整得非常大，这样就实现了对这个特征的直接记忆。相反，对于多层神经网络来说，特征会被多层处理，不断与其他特征进行交叉，因此模型对这个强特征的记忆反而没有简单模型深刻。

“泛化能力”可以被理解为模型传递特征的相关性，以及发掘稀疏甚至从未出现过的稀有特征与最终标签相关性的能力。矩阵分解比协同过滤的泛化能力强，因为矩阵分解引入了隐向量这样的结构，使得数据稀少的用户或者物品也能生成隐向量，从而获得有数据支撑的推荐得分，这就是非常典型的将全局数据传递到稀疏物品上，从而提高泛化能力的例子。再比如，深度神经网络通过特征的多次自动组合，可以深度发掘数据中潜在的模式，即使是非常稀疏的特征向量输入，也能得到较稳定平滑的推荐概率，这就是简单模型所缺乏的“泛化能力”。

Wide&Deep 模型的结构

Wide&Deep Wide EmbeddingDeep部分连接起来，一起输入最终的输出层。单层的Wide部分善于处理大量稀疏的id类特征；Deep部分利用神经网络表达能力强的特点，进行深层的特征交叉，挖掘藏在特征背后的数据模式。最终，利用逻辑回归模型，输出层将Wide部分和Deep部分组合起来，形成统一的模型。

在具体的特征工程和输入层设计中，展现了GooglePlay的推荐团队对业务场景的深刻理解。从图3-14中可以详细地了解到Wide&Deep模型到底将哪些特征作为Deep部分的输人，将哪些特征作为Wide部分的输入。

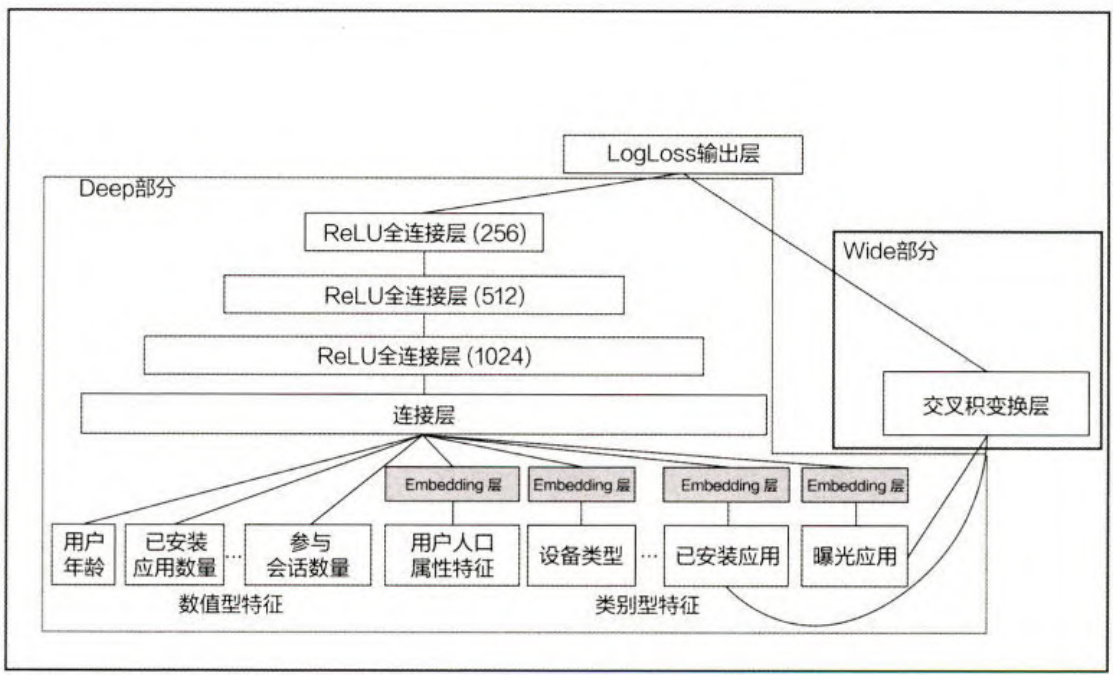
Deep部分的输人是全量的特征向量，包括用户年龄（Age）、已安装应用数量（#App Installs）、设备类型（Device Class）、已安装应用（User Installed App）曝光应用（ImpressionApp）等特征。已安装应用、曝光应用等类别型特征，需 Embedding（Concatenated Embedding），拼接成1200维的Embedding向量，再依次经过3层ReLU全连接层，最终输入LogLoss输出层。

Wide部分的输人仅仅是已安装应用和曝光应用两类特征，其中已安装应用代表用户的历史行为，而曝光应用代表当前的待推荐应用。选择这两类特征的原因是充分发挥Wide部分“记忆能力”强的优势。
Wide部分组合“已安装应用”和“曝光应用”两个特征的函数被称为交叉积变换（Cross Product Transformation）函数，其形式化定义如下所示。
∅ κ ( X ) = ∏ i = 1 d x i c k i c k i ∈ { 0 , 1 } \varnothing_{\kappa}(X)=\prod_{i=1}^{d}x_{i}^{c_{k i}}\quad c_{k i}\in\{0,1\} ∅κ​(X)=i=1∏d​xicki​​cki​∈{0,1}

$c_{ki}$ 是一个布尔变量，当第 $i$ 个特征属于第 $k$ 个组合特征时， $c_{ki}$ 的值为1，否则为0； $x_i$ 是第 $i$ 个特征的值。例如，对于“AND（user installed app $i=$ netfliximpression app $\mathfrak{e}=$ pandora)”这个组合特征来说，只有当“user installed app $=$ netflix’和“impression app $=$ pandora”这两个特征同时为1时，其对应的交叉积变换层的结果才为1，否则为0。

在通过交叉积变换层操作完成特征组合之后，Wide部分将组合特征输入最终的LogLoss输出层，与Deep部分的输出一同参与最后的目标拟合，完成Wide与Deep部分的融合。

Wide&Deep 模型的进化——Deep&Cross模型

在Wide&Deep模型之后，有越来越多的工作集中于分别改进Wide&Deep模型的Wide部分或是Deep部分。较典型的工作是2017年由斯坦福大学和谷歌的研究人员提出的Deep&Cross模型（DCN）。

Deep&Cross模型的结构图如图所示，其主要思路是使用Cross网络替代原来的Wide部分。

设计Cross网络的目的是增加特征之间的交互力度，使用多层交叉层（Crosslayer）对输人向量进行特征交叉。假设第I层交叉层的输出向量为 $x_l$ ，那么第 $l+1$ 层的输出向量如下所示。

$$x_{l+1}=x_0{x}_l^{\mathrm{T}}{W}_l+b_l+x_l$$

可以看到，交叉层操作的二阶部分非常类似于3.5节PNN模型中提到的外积操作，在此基础上增加了外积操作的权重向量 $w_l$ ，以及原输人向量 $x_l$ 和偏置向量 $b_{l\circ }$ 交叉层的操作如图所示。

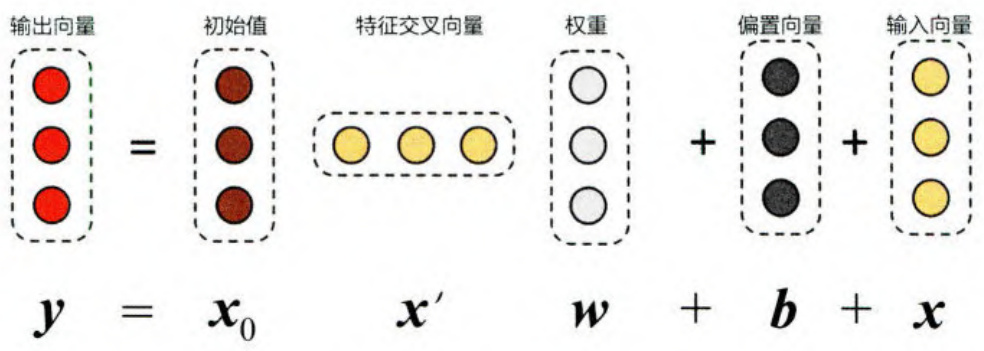
可以看出，交叉层在增加参数方面是比较“克制”的，每一层仅增加了一个 $n$ 维的权重向量 $w_l$ $n$ 维输人向量维度），并且在每一层均保留了输入向量，因此输出与输入之间的变化不会特别明显。由多层交叉层组成的Cross网络在Wide&Deep模型中Wide部分的基础上进行特征的自动化交叉，避免了更多基于业务理解的人工特征组合。同Wide&Deep模型一样，Deep&Cross模型的Deep部分相比Cross部分表达能力更强，使模型具备更强的非线性学习能力。

Wide&Deep模型的影响力

Wide&Deep模型能够取得成功的关键在于：

（1）抓住了业务问题的本质特点，能够融合传统模型记忆能力和深度学习模型泛化能力的优势。

（2）模型的结构并不复杂，比较容易在工程上实现、训练和上线，这加速了其在业界的推广应用。

也正是从Wide&Deep模型之后，越来越多的模型结构被加入推荐模型中，深度学习模型的结构开始朝着多样化、复杂化的方向发展。

FM与深度学习模型的结合

本节将介绍的FNN、DeepFM及NFM模型，使用不同的方式应用或改进了FM模型，并融合进深度学习模型中，持续发挥着其在特征组合上的优势。

FNN——用 FM 的隐向量完成 Embedding 层初始化

FNN类似于DeepCrossing模型，关键在于Embedding层的改进。

在神经网络的参数初始化过程中，往往采用随机初始化这种不包含任何先验信息的初始化方法。由于Embedding层的输入极端稀疏化，导致Embedding层的收敛速度非常缓慢。再加上Embedding层的参数数量往往占整个神经网络参数数量的大半以上，因此模型的收敛速度往往受限于Embedding层。

为什么Embedding层的收敛速度往往很慢

在深度学习网络中，Embedding层的作用是将稀疏输人向量转换成稠密向量，但Embedding层的存在往往会拖慢整个神经网络的收敛速度，原因有两个：

（1）Embedding层的参数数量巨大。这里可以做一个简单的计算。假设输人层的维度是100,000，Embedding层输出维度是32，上层再加5层32维的全连接层，最后输出层维度是10，那么输人层到Embedding层的参数数量是 $32\times 100,000=3,200,000$ ，其余所有层的参数总数是 $(32\times 32)\times 4+32\times 10=4416$ 。那么，Embedding层的权重总数占比是 $3,200,000/(3,200,000+4416)=99.86\%$

也就是说，Embedding层的权重占了整个网络权重的绝大部分。那么，训练过程可想而知，大部分的训练时间和计算开销都被Embedding层占据。

（2）由于输入向量过于稀疏，在随机梯度下降的过程中，只有与非零特征相连的Embedding层权重会被更新（请参照随机梯度下降的参数更新公式理解），这进一步降低了Embedding层的收敛速度。

针对Embedding层收敛速度的难题，FNN模型的解决思路是用FM模型训练好的各特征隐向量初始化Embedding层的参数，相当于在初始化神经网络参数时，已经引入了有价值的先验信息。下图是FM各参数和FNN中Embedding层各参数的对应关系：

DeepFM——用 FM 代替 Wide 部分

DeepFM对Wide&Deep模型的改进之处在于，它用FM替换了原来的Wide部分，加强了浅层网络部分特征组合的能力。FM部分对不同的特征域的Embedding进行了两两交叉，也就是将Embedding向量当作原FM中的特征隐向量。最后将FM的输出与 Deep 部分的输出一同输人最后的输出层，参与最后的目标拟合。这里的改进动机与Deep&Cross模型的完全一致，唯一的不同就在于Deep&Cross模型利用多层Cross网络进行特征组合，而DeepFM模型利用FM进行特征组合。

NFM——FM 的神经网络化尝试

在数学形式上，NFM模型的主要思路是用一个表达能力更强的函数替代原FM中二阶隐向量内积的部分。

NFM网络架构的特点非常明显，就是在Embedding层和多层神经网络之间加入特征交叉池化层（Bi-Interaction Pooling Layer）。假设 $V_x$ 是所有特征域的Embedding集合，那么特征交叉池化层的具体操作如下所示。

$$f_{\mathrm{BI}}(V_x)=\sum _{i=1}^n\sum _{j=i+1}^n(x_i{v}_i)\odot (x_j{v}_j)$$

其中， $\odot$ 代表两个向量的元素积操作，即两个长度相同的向量对应维相乘得到元素积向量，其中第 $k$ 维的操作如下所示。

$${\left(v_i\odot v_j\right)}_k={\nu }_{ik}{\nu }_{jk}$$

在进行两两Embedding向量的元素积操作后，对交叉特征向量取和，得到池化层的输出向量。再把该向量输入上层的多层全连接神经网络，进行进一步的交 叉。

如果把NFM的一阶部分视为一个线性模型，那么NFM的架构也可以视为Wide&Deep模型的进化。相比原始的Wide&Deep模型，NFM模型对其Deep部分加人了特征交叉池化层，加强了特征交叉。这是理解NFM模型的另一个角度。

基于 FM 的深度学习模型的优点和局限性

在经典多层神经网络的基础上加入有针对性的特征交义操作，让模型具备更强的非线性表达能力。

沿着特征工程自动化的思路，深度学习模型从PNN一路走来，经过了Wide&Deep、Deep&Cross、FNN、DeepFM、NFM等模型，进行了大量的、基于不同特征互操作思路的尝试。但特征工程的思路走到这里几乎已经穷尽了可能的尝试，模型进一步提升的空间非常小，这也是这类模型的局限性所在。

从这之后，越来越多的深度学习推荐模型开始探索更多“结构”上的尝试，诸如注意力机制、序列模型、强化学习等在其他领域大放异彩的模型结构也逐渐进入推荐系统领域，并且在推荐模型的效果提升上成果显著。

注意力机制在推荐模型中的应用

AFM 引入注意力机制的 FM

AFM模型可以被认为是NFM模型的延续。在NFM模型中，不同域的特征Embedding向量经过特征交叉池化层的交叉，将各交叉特征向量进行“加和”，输入最后由多层神经网络组成的输出层。问题的关键在于加和池化（SumPooling）操作，它相当于“一视同仁”地对待所有交叉特征，不考虑不同特征对结果的影响程度，事实上消解了大量有价值的信息。

这里“注意力机制”就派上了用场，它基于假设一不同的交叉特征对于结果的影响程度不同，以更直观的业务场景为例，用户对不同交叉特征的关注程度应是不同的。

DIN——引入注意力机制的深度学习网络

相比于之前很多“学术风”的深度学习模型，阿里巴巴提出的DIN模型显然更具业务气息。它的应用场景是阿里巴巴的电商广告推荐，因此在计算一个用户u是否点击一个广告a时，**模型的输入特征自然分为两大部分：一部分是用户u的特征组，另一部分是候选广告a的特征组。**无论是用户还是广告，都含有两个非常重要的特征一商品id（good_id）和商铺id（shop_id）。用户特征里的商品id是一个序列，代表用户曾经点击过的商品集合，商铺id同理；而广告特征里的商品id和商铺id就是广告对应的商品id和商铺id（阿里巴巴平台上的广告大部分是参与推广计划的商品）。

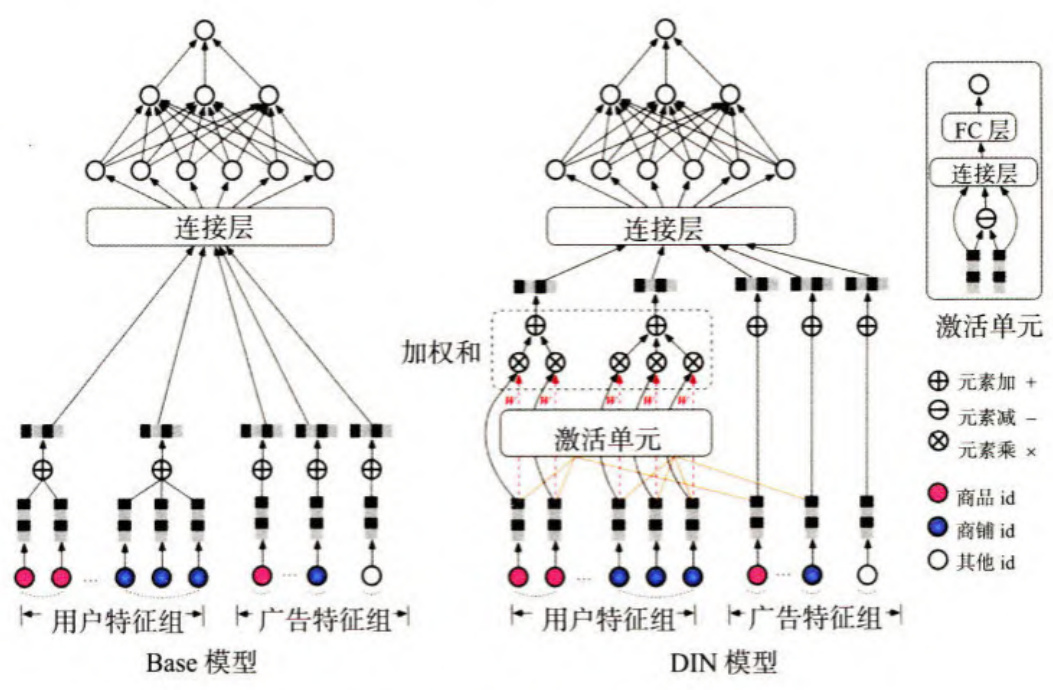
在原来的基础模型中（Base模型），用户特征组中的商品序列和商铺序列经过简单的平均池化操作后就进人上层神经网络进行下一步训练，序列中的商品既没有区分重要程度，也和广告特征中的商品id没有关系。

将上述“注意力”的思想反映到模型中也是直观的。利用候选商品和历史行为商品之间的相关性计算出一个权重，这个权重就代表了“注意力”的强弱，加人了注意力权重的深度学习网络就是DIN模型，其中注意力部分的形式化表达如下所示。

$$V_{\mathrm{u}}=f(V_{\mathrm{a}})=\sum _{i=1}^N{w}_i\cdot V_i=\sum _{i=1}^{N}g(V_i,V_{\mathrm{a}})\cdot V_i$$

其中， $V_{\mathrm{u}}$ Embedding， $V_a$ 是候选广告商品的Embedding向量，

$V_i$ 是用户 $\mathbf{u}$ 的第 $i$ 次行为的Embedding向量。这里用户的行为就是浏览商品或店铺，因此行为的Embedding向量就是那次浏览的商品或店铺的Embedding向量。

因为加人了注意力机制，所以 $V_{\mathrm{u}}.$ 从过去 $V_i$ 的加和变成了 $V_i$ 的加权和， $V_i$ 的权重 $w_i$ 就由 $V_i$ 与 $V_a$ 的关系决定，也就是式中的 $g(V_i,V_a)$ ，即“注意力得分”。

那么， $g(V_i,V_a)$ 函数到底采用什么形式比较好呢？答案是使用一个注意力激活单元（activationunit）来生成注意力得分。这个注意力激活单元本质上也是一个小的神经网络，其具体结构如图3-24右上角处的激活单元所示。

可以看出，激活单元的输人层是两个Embedding向量，经过元素减（element-wiseminus）操作后，Embedding输入，最后通过单神经元输出层生成注意力得分。

如果留意图中的红线，可以发现商铺id只跟用户历史行为中的商铺id序列发生作用，商品id只跟用户的商品id序列发生作用，因为注意力的轻重更应该由同类信息的相关性决定。

DIN模型与基于FM的AFM模型相比，是一次更典型的改进深度学习网络的尝试，而且由于出发点是具体的业务场景，也给了推荐工程师更多实质性的启发。

注意力机制对推荐系统的启发

**注意力机制在数学形式上只是将过去的平均操作或加和操作换成了加权和或者加权平均操作。这一机制对深度学习推荐系统的启发是重大的。**因为“注意力得分”的引入反映了人类天生的“注意力机制”特点。对这一机制的模拟，使得推荐系统更加接近用户真实的思考过程，从而达到提升推荐效果的目的。

从“注意力机制”开始，越来越多对深度学习模型结构的改进是基于对用户行为的深刻观察而得出的。相比学术界更加关注理论上的创新，业界的推荐工程师更需要基于对业务的理解推进推荐模型的演化。

DIEN——序列模型与推荐系统的结合

阿里巴巴在2019年提出DIN模型的演化版本——DIEN。DIEN 模型的应用场景和DIN完全一致，其创新在于用序列模型模拟了用户兴趣的进化过程。

DIEN 的进化动机

无论是电商购买行为，还是视频网站的观看行为，或是新闻应用的阅读行为，特定用户的历史行为都是一个随时间排序的序列。既然是时间相关的序列，就一定存在或深或浅的前后依赖关系，这样的序列信息对于推荐过程无疑是有价值的。但本章之前介绍的所有模型，有没有利用到这层序列信息呢？答案是否定的。即使是引人了注意力机制的AFM或DIN模型，也仅是对不同行为的重要性进行打分，这样的得分是时间无关的，是序列无关的。

例如，上周一位用户在挑选一双篮球鞋，这位用户上周的行为序列都会集中在篮球鞋这个品类的商品上，但在他完成购买后，本周他的购物兴趣可能变成买一个机械键盘。

序列信息的重要性在于：

（1）它加强了最近行为对下次行为预测的影响。在这个例子中，用户近期购买机械键盘的概率会明显高于再买一双篮球鞋或购买其他商品的概率。

（2）序列模型能够学习到购买趋势的信息。在这个例子中，序列模型能够在一定程度上建立“篮球鞋”到“机械键盘”的转移概率。如果这个转移概率在全局统计意义上是足够高的，那么在用户购买篮球鞋时，推荐机械键盘也会成为一个不错的选项。直观上，二者的用户群体很有可能是一致的。

**如果放弃序列信息，则模型学习时间和趋势这类信息的能力就不会那么强，推荐模型就仍然是基于用户所有购买历史的综合推荐，而不是针对“下一次购买推荐。**显然，从业务的角度看，后者才是推荐系统正确的推荐目标。

DIEN 模型的架构

模型仍是输人层+Embedding层 $+$ 连接层 $+$ 多层全连接神经网络 $+$ 输出层的整体架构。图中彩色的“兴趣进化网络”被认为是一种用户兴趣的Embedding方法，它最终的输出是 $h^{\prime }(T)$ 这个用户兴趣向量。

兴趣进化网络分为三层，从下至上依次是：

（1）行为序列层（BehaviorLayer，浅绿色部分）：其主要作用是把原始的id类行为序列转换成Embedding行为序列。（2）兴趣抽取层（InterestExtractorLayer，米黄色部分）：其主要作用是通过模拟用户兴趣迁移过程，抽取用户兴趣。（3）兴趣进化层（InterestEvolvingLayer，浅红色部分）：其主要作用是通过在兴趣抽取层基础上加入注意力机制，模拟与当前目标广告相关的兴趣进化过程。

在兴趣进化网络中，行为序列层的结构与普通的Embedding层是一致的，模拟用户兴趣进化的关键在于“兴趣抽取层”和“兴趣进化层”。

兴趣抽取层的结构

兴趣抽取层的基本结构是GRU（GatedRecurrentUnit，门循环单元）网络。相比传统的序列模型 RNN（Recurrent Neural Network，循环神经网络）和LSTM （LongShort-TermMemory，长短期记忆网络），GRU解决了RNN的梯度消失问题。与LSTM相比，GRU的参数数量更少，训练收敛速度更快，因此成了DIEN序列模型的选择。
每个GRU单元的具体形式由系列公式定义。

$$\begin{array}{rl}& u_t=\sigma (W^u{i}_t+U^u{h}_{t-1}+b^u)\\ & r_t=\sigma (W^r{i}_t+U^r{h}_{t-1}+b^r)\\ & \widetilde{h_t}=\tanh (W^h{i}_t+r_t\circ U^h{h}_{t-1}+b^h)\\ & h_t=(1-u_t)\circ h_{t-1}+u_t\circ {\tilde{h}}_t\end{array}$$

其中， $\sigma$ 是Sigmoid激活函数，·是元素积操作， $W^u,W^r,W^h,U^z,U^r,U^h$ 是6组需要学习的参数矩阵， $i_t$ 是输人状态向量，也就是行为序列层的各行为Embedding $b(t)$ ， $h_t$ 是GRU网络中第 $t$ 个隐状态向量。

经过由GRU组成的兴趣抽取层后，用户的行为向量 $b(t)$ 被进一步抽象化，形成了兴趣状态向量 $h(t)$ 。理论上，在兴趣状态向量序列的基础上，GRU网络已经可以做出下一个兴趣状态向量的预测，但DIEN却进一步设置了兴趣进化层，这是为什么呢？

兴趣进化层的结构

兴趣进化层注意力得分的生成过程与DIN完全一致，都是当前状态向量与自标厂告向量进行互作用的结果。也就是说，DIEN在模拟兴趣进化的过程中，需要考虑与目标广告的相关性。

**在兴趣抽取层之上再加上兴趣进化层就是为了更有针对性地模拟与目标广告相关的兴趣进化路径。**由于阿里巴巴这类综合电商的特点，用户非常有可能同时购买多品类商品，例如在购买“机械键盘”的同时还在查看“衣服”品类下的商品，那么这时注意力机制就显得格外重要了。当目标广告是某个电子产品时，用户购买“机械键盘”相关的兴趣演化路径显然比购买“衣服”的演化路径重要，这样的筛选功能兴趣抽取层没有。

兴趣进化层完成注意力机制的引入是通过AUGRU（GRU with Attentional Update gate，基于注意力更新门的GRU）结构，具体形式如下所示。
$$\begin{array}{rl}& {\tilde{u}}_t^{\prime }=a_t\cdot u_t^{\prime }\\ & h_t^{\prime }=(1-{\tilde{u}}_t^{\prime })\circ h_{t-1}^{\prime }+{\tilde{u}}_t^{\prime }\circ {\tilde{h}}_t^{\prime }\end{array}$$

可以看出AUGRU在原始的 $u_t^{\prime }$ ［原始更新门向量中的 $u_t$ 门基础上加人了注意力得分 $a_t$ ，注意力得分的生成方式与DIN模型中注意力激活单元的基本一致。

序列模型对推荐系统的启发

由于序列模型具备强大的时间序列的表达能力，使其非常适合预估用户经过一系列行为后的下一次动作。

事实上，不仅阿里巴巴在电商模型上成功运用了序列模型，YouTube、Netflix等视频流媒体公司也已经成功的在其视频推荐模型中应用了序列模型，用于预测用户的下次观看行为（nextwatch）。

但在工程实现上需要注意：序列模型比较高的训练复杂度，以及在线上推断过程中的串行推断，使其在模型服务过程中延迟较大，这无疑增大了其上线的难度，需要在工程上着重优化。

DRN——强化学习与推荐系统的结合

强化学习（ReinforcementLearning）是近年来机器学习领域非常热门的研究话题，它的研究起源于机器人领域，针对智能体（Agent）在不断变化的环境（Environment）中决策和学习的过程进行建模。在智能体的学习过程中，会完成收集外部反馈（Reward），改变自身状态（State），再根据自身状态对下一步的行动（Action）进行决策，在行动之后持续收集反馈的循环，简称“行动-反馈-状态更新”的循环。

2018年，由宾夕法尼亚州立大学和微软亚洲研究院的学者提出的推荐领域的强化学习模型DRN，就是一次将强化学习应用于新闻推荐系统的尝试。

深度强化学习推荐系统框架

智能体：推荐系统本身，它包括基于深度学习的推荐模型、探索（explore）策略，以及相关的数据存储（memory）。

环境：由新闻网站或App、用户组成的整个推荐系统外部环境。在环境中，用户接收推荐的结果并做出相应反馈。
行动：对一个新闻推荐系统来说，“行动”指的就是推荐系统进行新闻排序后推送给用户的动作。

反馈：用户收到推荐结果后，进行正向的或负向的反馈。例如，点击行为被认为是一个典型的正反馈，曝光未点击则是负反馈的信号。此外，用户的活跃程度，用户打开应用的间隔时间也被认为是有价值的反馈信号。

状态：状态指的是对环境及自身当前所处具体情况的刻画。在新闻推荐场景中，状态可以被看作已收到所有行动和反馈，以及用户和新闻的所有相关信息的特征向量表示。站在传统机器学习的角度，“状态”可以被看作已收到的、可用于训练的所有数据的集合。

在这样的强化学习框架下，模型的学习过程可以不断地选代，迭代过程主要有如下几步：

（1）初始化推荐系统（智能体）

（2）推荐系统基于当前已收集的数据（状态）进行新闻排序（行动），并推送到网站或App（环境）中。

（3）用户收到推荐列表，点击或者忽略（反馈）某推荐结果。

（4）推荐系统收到反馈，更新当前状态或通过模型训练更新模型。

（5）重复第2步。

强化学习相比传统深度模型的优势就在于强化学习模型能够进行“在线学习”，不断利用新学到的知识更新自己，及时做出调整和反馈。这也正是将强化学习应用于推荐系统的收益所在。

深度强化学习推荐模型

智能体部分是强化学习框架的核心，对推荐系统这一智能体来说，推荐模型是推荐系统的“大脑”。在DRN框架中，扮演“大脑”角色的是DeepQ-Network（深度Q网络，简称DQN），其中Q是Quality的简称，指通过对行动进行质量评估，得到行动的效用得分，以此进行行动决策。
DON的网络结构如图所示，在特征工程中套用强化学习状态向量和行动向量的概念，把用户特征（user features）和环境特征（context features）归为状态向量，因为它们与具体的行动无关：把用户-新闻交叉特征和新闻特征归为行动特征，因为其与推荐新闻这一行动相关。

用户特征和环境特征经过左侧多层神经网络的拟合生成价值（value）得分 $V(s)$ ，利用状态向量和行动向量生成优势（advantage）得分 $A(s,a)$ ，最后把两部分得分综合起来，得到最终的质量得分 $Q(s,a)$

价值得分和优势得分都是强化学习中的概念，在理解DQN时，读者不必过多纠结这些名词，只要清楚DQN的结构即可。事实上，任何深度学习模型都可以作为智能体的推荐模型，并没有特殊的建模方面的限制。

DRN 的学习过程

按照从左至右的时间顺序，依次描绘DRN学习过程中的重要步骤。

（1）在离线部分，根据历史数据训练好DQN模型，作为智能体的初始化模型。（2）在 $t_1\to t_2$ 阶段，利用初始化模型进行一段时间的推送（push）服务，积累反馈（feedback）数据。(3）在 $t_2$ 时间点，利用 $t_1\to t_2$ 阶段积累的用户点击数据，进行模型微更新（minorupdate) （4）在 $t_4$ 时间点，利用 $t_1\to t_4$ 阶段的用户点击数据及用户活跃度数据进行模型的主更新（major update）。

（5）重复第2~4步。

在第4步中出现的模型主更新操作可以理解为利用历史数据的重新训练，用训练好的模型替代现有模型。那么在第3步中提到的模型微调怎么操作呢？这就牵扯到DRN使用的一种新的在线训练方法——竞争梯度下降算法（DuelingBand it Gradient Descent Algorithm) 。

DRN 的在线学习方法——竞争梯度下降算法

其主要步骤如下：

（1）对于已经训练好的当前网络 $Q$ ，对其模型参数 $W$ 添加一个较小的随机扰动$△W$，得到新的模型参数$\tilde{W}$，这里称W对应的网络为探索网络 $\tilde{Q}$

（2）对于当前网络 $Q$ 和探索网络 $\tilde{Q}$ ，分别生成推荐列表 $L$ 和 $\tilde{L}$ ，用Interleaving（后续章节介绍）将两个推荐列表组合成一个推荐列表后推送给用户。

（3）实时收集用户反馈。如果探索网络Q生成内容的效果好于当前网络 $\mathcal{Q}$ 则用探索网络代替当前网络，进入下一轮选代；反之则保留当前网络。

在第1步中，由当前网络 $Q$ 生成探索网络 $\tilde{Q}$ ，产生随机扰动的公式。
$$△W=\alpha \ast rand(-1,1)\ast W$$
其中，α是探索因子，决定探索力度的大小。rand(-1,1)是一个[-1,1]之间的随机数。

DRN的在线学习过程利用了“探索”的思想，其调整模型的粒度可以精细到每次获得反馈之后，这一点很像随机梯度下降的思路，虽然一次样本的结果可能产生随机扰动，但只要总的下降趋势是正确的，就能通过海量的尝试最终达到最优点。DRN正是通过这种方式，让模型时刻与最“新鲜”的数据保持同步，将最新的反馈信息实时地融人模型中。

强化学习对推荐系统的启发

强化学习在推荐系统中的应用可以说又一次扩展了推荐模型的建模思路。它与之前提到的其他深度学习模型的不同之处在于变静态为动态，把模型学习的实时性提到了一个空前重要的位置。

它也给我们提出了一个值得思考的问题一到底是应该打造一个重量级的、“完美”的，但训练延迟很大的模型；还是应该打造一个轻巧的、简单的，但能够实时训练的模型。当然，工程上的事情没有假设，更没有猜想，只通过实际效果说话，“重量”与“实时”之间也绝非对立关系，但在最终决定一个技术方案之前，这样的思考是非常必要的，也是值得花时间去验证的。

总结