LabVIEW 实现 find_nearest_neighbors 功能(二维平面上的最近邻查找)
1. 背景介绍
在数据分析和图像处理领域,经常需要查找给定点的最近邻居点。在LabVIEW中,计算二维平面上多个点之间的欧氏距离,并返回距离最近的几个点是一种常见操作。find_nearest_neighbors 函数用于实现这个功能。
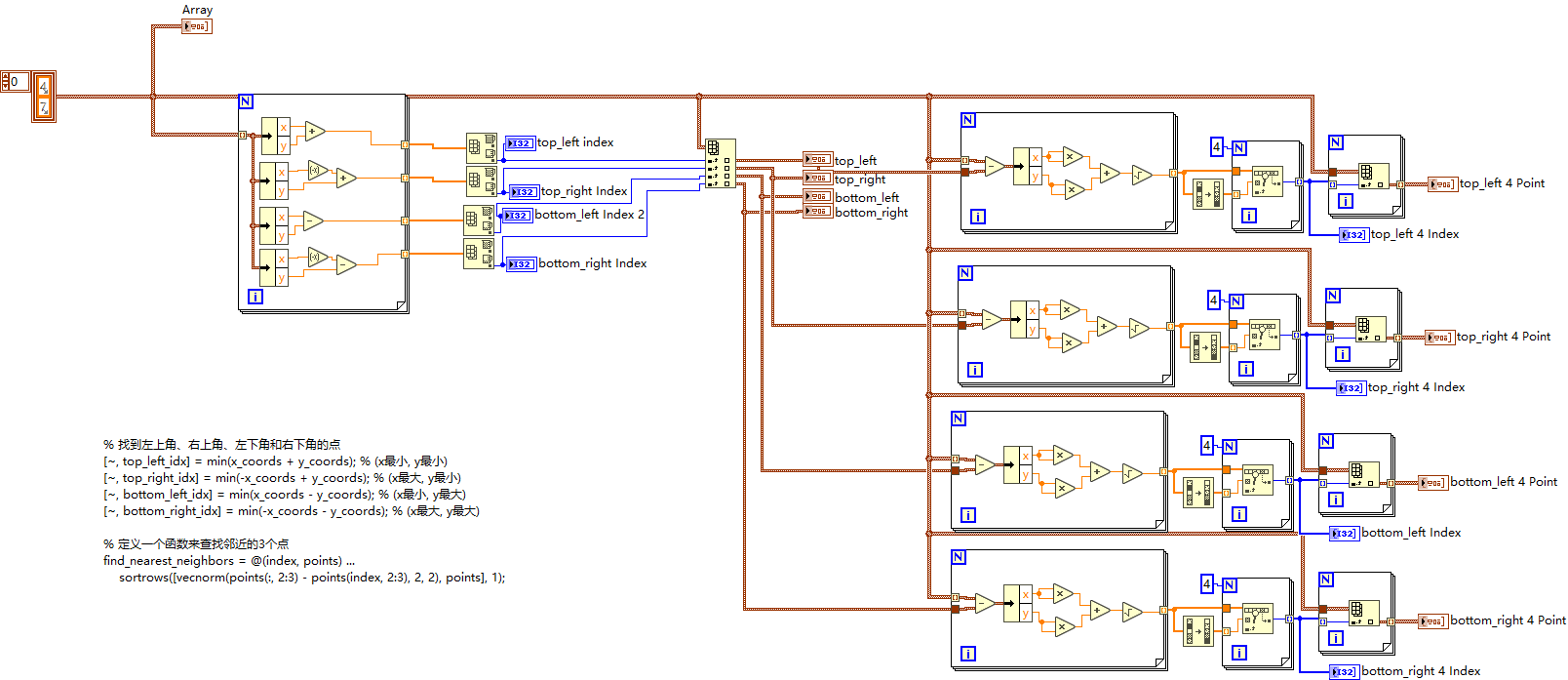
2. 欧氏距离计算
在二维平面上,两个点 (x1,y1)(x1,y1) 和 (x2,y2)(x2,y2) 之间的欧氏距离公式为:
D=(x2−x1)2+(y2−y1)2D=(x2−x1)2+(y2−y1)2
3. 实现步骤
步骤概述:
-
输入:给定一个参考点和一个包含其他点的数组。
-
计算:使用欧氏距离公式计算参考点与数组中每个点的距离。
-
排序:将所有计算的距离进行排序。
-
输出:提取排序后的前3个最小距离点。
具体操作:
-
For Loop:使用
For Loop遍历点数组。-
使用
Subtract计算 x 和 y 坐标差值。 -
使用
Square计算差值的平方。 -
使用
Add求平方和,再通过Sqrt计算平方根得到距离。
-
-
排序:将所有计算得到的距离存入数组,使用
Sort 1D Array对其升序排序。 -
提取最小3个距离:
-
使用
Array Subset提取排序后的前3个最小距离点。
-
4. 使用的LabVIEW函数
-
Subtract:计算两个点坐标的差。
-
Square:计算差值的平方。
-
Add:累加平方后的差值。
-
Sqrt:求平方根,得到欧氏距离。
-
Sort 1D Array:对距离进行排序。
-
Array Subset:提取前3个最近的点。
5. 应用场景
-
图像处理:用于识别图像中最接近的特征点。
-
数据分析:用于聚类分析中的最近邻查找。
-
机器人路径规划:用于计算目标点的最优路径。
通过上述方法,LabVIEW可以高效地实现二维平面上点的最近邻查找,满足工程项目中对数据处理的需求。
