当前位置：首页 > article >正文

数据结构与算法基础-学习-18-哈夫曼编码

article 2025/1/20 18:33:11

一、个人理解

在远程通讯中，需要把字符转成二进制的字符串进行传输，例如我们需要传输ABCD，我们可以用定长的字符串进行表示，例如:

A:00

B:01

C:02

D:03

这样可能就造成空间的浪费，我们多存储了一个0号位。那用变长呢，会怎么样，我们试试，例如：

B:00

C:01

如果接收到的二进制字符串为：0000101，在解码时是否就会出现歧义，可以是AAAADAD,也可以是ABCC，也可以是BBDC等等。

从而引入了哈夫曼编码，也称为最优前缀码。之前我们已经实现了哈夫曼树，可以参考文章链接《数据结构与算法基础-学习-17-二叉树之哈夫曼树》，从哈夫曼树这个中间结果，转换出我们想要的哈夫曼编码。

二、为什么哈夫曼编码得出二进制字符串最短呢？

在生成哈夫曼树之前，我们需要统计字符在数据中出现的概率，出现的概率越高，编码会越短。

之前介绍过的哈夫曼树的特点，权值越大的结点离根结点越近，也就是路径越短。

哈夫曼树规定走左子树就标记为0，走右子树就标记为1，从根结点到各个叶子节点的标记拼接起来，就是这个字符的哈夫曼编码。

三、结构体定义

typedef char** HaffmanCode;

四、函数实现

1、生成哈夫曼编码

（1）定义

Status CreateHaffmanCode(HaffmanTree HT, HaffmanCode* HC, HaffmanTreeLentype ArrayLen)
{
    JudgeAllNullPointer(HT);

    //Init HaffmanCode
    *HC          = (HaffmanCode)MyMalloc(sizeof(char*) * ArrayLen);

    char* TmpHC = (char*)MyMalloc(sizeof(char) * (ArrayLen - 1));//临时数组存放哈夫曼编码中间结果,长度n，编码最长需要n-1,所以分配n-1。
    HaffmanTreeLentype TmpHCLen = 0;

    HaffmanTreeLentype i,j;
    HaffmanTreeLentype TmpParentIndex;//上一个结点的父亲索引。
    HaffmanTreeLentype TmpIndex;//上一个结点的索引号。

    for(i = 1; i <= ArrayLen; i++)
    {
        TmpParentIndex = HT[i].ParentIndex;
        TmpIndex       = i;
        while(HT[TmpParentIndex].ParentIndex != 0)
        {
            if(HT[TmpParentIndex].LeftChildIndex == TmpIndex)
            {
                TmpHC[TmpHCLen] = '0';
                TmpHCLen++;
            }
            else if (HT[TmpParentIndex].RightChildIndex == TmpIndex)
            {
                TmpHC[TmpHCLen] = '1';
                TmpHCLen++;
            }
            else
            {
                Log("Internal Error : Perant LeftChildIndex and RightChildIndex != TmpIndex",Error);
            }
            TmpIndex       = TmpParentIndex;
            TmpParentIndex = HT[TmpParentIndex].ParentIndex;
        }
        
        //根节点判断
        if(HT[TmpParentIndex].LeftChildIndex == TmpIndex)
        {
            TmpHC[TmpHCLen] = '0';
            TmpHCLen++;
        }
        else if(HT[TmpParentIndex].RightChildIndex == TmpIndex)
        {
            TmpHC[TmpHCLen] = '1';
            TmpHCLen++;
        }
        else
        {
            Log("Internal Error : Root Node Perant LeftChildIndex and RightChildIndex != TmpIndex",Error);
        }

        //将TmpHC中的字符倒序写入HC中。
        (*HC)[i-1] = (char*)MyMalloc(sizeof(char) * (TmpHCLen + 1));//编码最长需要n,加上\0，所以分配n+1。
        for(j = TmpHCLen - 1; j >= 0; j--)
        {
            (*HC)[i-1][TmpHCLen - 1 - j] = TmpHC[j];
            if(j == 0)//因为j是无符号长整型，j不能等于负数，当j=-1,退出循环，导致程序core掉，由此添加此判断，避免问题的发生。
            {
                break;
            }
        }
        (*HC)[i-1][TmpHCLen] = '\0';
        TmpHCLen             = 0;
    }
    free(TmpHC);
    TmpHC = NULL;
    Log("Create HaffmanCode     : OK\n",Info);
    return SuccessFlag;
}

（2）参数

参数名	说明
HT	传入参数类型为HaffmanTree 的哈夫曼树。
HC	传入参数类型为HaffmanCode*的哈夫曼编码数组指针。
ArrayLen	传入参数类型为HaffmanTreeLentype的权值数组长度。

（3）实现思路

A,B,C,D,E对应的权值如下：

HaffmanTreeLentype WeightArray[]  = {2,4,2,3,3};

生成哈夫曼树如下：

2023-3--[Info]--HaffmanTree            :
[ Index | Weight | ParentIndex | LeftChildIndex | RightChildIndex ]
[ 0     | 0      | 0           | 0              | 0               ]
[ 1     | 2      | 6           | 0              | 0               ]
[ 2     | 4      | 8           | 0              | 0               ]
[ 3     | 2      | 6           | 0              | 0               ]
[ 4     | 3      | 7           | 0              | 0               ]
[ 5     | 3      | 7           | 0              | 0               ]
[ 6     | 4      | 8           | 1              | 3               ]
[ 7     | 6      | 9           | 4              | 5               ]
[ 8     | 8      | 9           | 6              | 2               ]
[ 9     | 14     | 0           | 7              | 8               ]

图示如下：

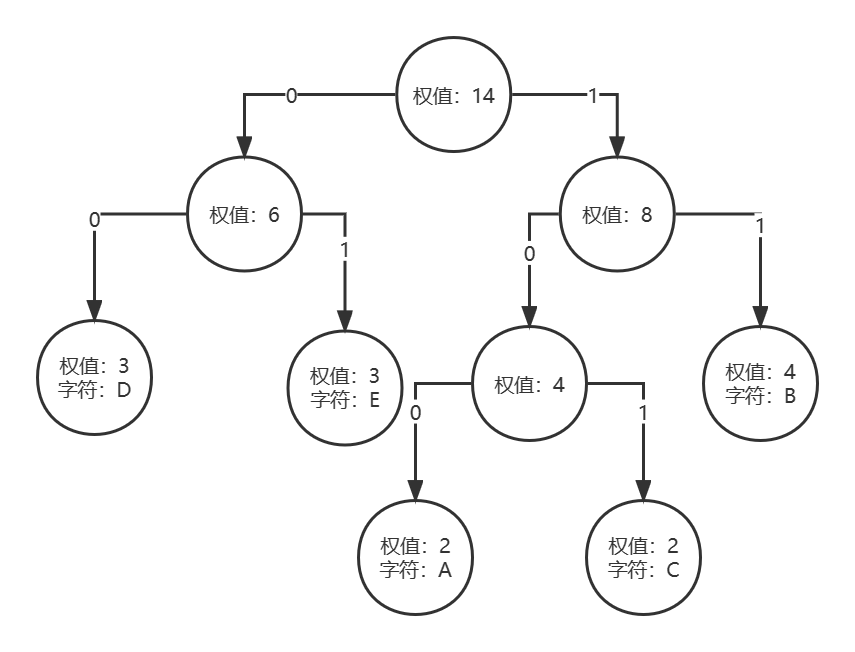
从根节点开始遍历到每个叶子结点算出哈夫曼编码比较困难，我们反其道而行之，从叶子结点开始遍历到根节点，但我们算出的结果是一个倒序的，我们需要一个临时数组来存储倒序编码，最后再正序填写回哈夫曼编码数组中即可。

例如我们来算一个A，父亲是权值4，走左子树为0，0写入临时数组,

char TmpHC[] = {'0'};

再往上走，父亲是权值8，走左子树为0，0写入临时数组，

char TmpHC[] = {'0','0'};

再往上走，父亲是权值14，走右子树为1，1写入临时数组，

char TmpHC[] = {'0','0','1'};

倒序写回哈夫曼编码数组就是100。其他的大家自己可以算一下，是不是这样，至于和老师讲的可能有不一样的地方，例如最后形成的编码，只是由于数组中选出两个最小的值，哪个是左子树索引，哪个是右子树索引，不一样导致，但不影响编码。最终得出的哈夫曼编码如下：

2023-3--[Info]--HaffmanCode            :
[ Index | Code    ]
[ 1     | 100     ]
[ 2     | 11      ]
[ 3     | 101     ]
[ 4     | 00      ]
[ 5     | 01      ]

2、销毁哈夫曼编码

（1）定义

Status DestoryHaffmanCode(HaffmanCode HC,HaffmanTreeLentype ArrayLen)
{
    JudgeAllNullPointer(HC);
    HaffmanTreeLentype i;
    for(i = 0; i < ArrayLen; i++)
    {
        free(HC[i]);
        HC[i] = NULL;
    }
    free(HC);
    HC = NULL;
    Log("Destory HaffmanCode    : OK\n",Info);
    return SuccessFlag;
}

（2）参数

参数名	说明
HC	传入参数类型为HaffmanCode*的哈夫曼编码数组指针。
ArrayLen	传入参数类型为HaffmanTreeLentype的权值数组长度。

五、虚机测试

[gbase@czg2 Tree]$ make
gcc -Wall -g ../Log/Log.c BinaryTree.c HaffmanTree.c main.c -o TestBinaryTree -I ../Log/
[gbase@czg2 Tree]$ ./TestBinaryTree 
2023-3--[Info]--Init Global Array      : OK
2023-3--[Info]--Init Binary Tree       : OK
2023-3--[Info]--New Binary Search Tree : OK
2023-3--[Info]--PreOrderTraverse       : [6 ,3 ,2 ,1 ,5 ,8 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverse        : [1 ,2 ,3 ,5 ,6 ,7 ,8 ], CurSize : 7
2023-3--[Info]--PostOrderTraverse      : [1 ,2 ,5 ,3 ,7 ,8 ,6 ], CurSize : 7
2023-3--[Info]--PreOrderTraverseNoRcs  : [6 ,3 ,2 ,1 ,5 ,8 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverseNoRcs   : [1 ,2 ,3 ,5 ,6 ,7 ,8 ], CurSize : 7
2023-3--[Info]--PostOrderTraverseNoRcs : [1 ,2 ,5 ,3 ,7 ,8 ,6 ], CurSize : 7
2023-3--[Info]--LevelOrderBinaryTree   : [6 ,3 ,8 ,2 ,5 ,7 ,1 ], CurSize : 7
2023-3--[Info]--SqQueue Data           :
Data           : [1 ,2 ,3 ,0 ,0 ,4 ,5 ,0 ,6 ,0 ,0 ,7 ,0 ,0 ,0 ]
FrontIndex     : 0
RearIndex      : 15
SqQueueLen     : 15
2023-3--[Info]--Init Binary Tree       : OK
2023-3--[Info]--PreOrderTraverse       : [1 ,2 ,3 ,4 ,5 ,6 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverse        : [3 ,2 ,5 ,6 ,4 ,7 ,1 ], CurSize : 7
2023-3--[Info]--PostOrderTraverse      : [3 ,6 ,5 ,7 ,4 ,2 ,1 ], CurSize : 7
2023-3--[Info]--PreOrderTraverseNoRcs  : [1 ,2 ,3 ,4 ,5 ,6 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverseNoRcs   : [3 ,2 ,5 ,6 ,4 ,7 ,1 ], CurSize : 7
2023-3--[Info]--PostOrderTraverseNoRcs : [3 ,6 ,5 ,7 ,4 ,2 ,1 ], CurSize : 7
2023-3--[Info]--LevelOrderBinaryTree   : [1 ,2 ,3 ,4 ,5 ,7 ,6 ], CurSize : 7
2023-3--[Info]--Init Binary Tree       : OK
2023-3--[Info]--Copy Tree              : OK
2023-3--[Info]--PreOrderTraverse       : [1 ,2 ,3 ,4 ,5 ,6 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverse        : [3 ,2 ,5 ,6 ,4 ,7 ,1 ], CurSize : 7
2023-3--[Info]--PostOrderTraverse      : [3 ,6 ,5 ,7 ,4 ,2 ,1 ], CurSize : 7
2023-3--[Info]--Tree Depth             : 4
2023-3--[Info]--Tree Depth             : 5
2023-3--[Info]--Tree Depth             : 5
2023-3--[Info]--Tree Node Num          : 7
2023-3--[Info]--Tree Node Num          : 7
2023-3--[Info]--Tree Node Num          : 7
2023-3--[Info]--Tree Leaves Node Num   : 3
2023-3--[Info]--Tree Leaves Node Num   : 3
2023-3--[Info]--Tree Leaves Node Num   : 3
2023-3--[Info]--Create HaffmanTree     : OK
2023-3--[Info]--HaffmanTree            :
[ Index | Weight | ParentIndex | LeftChildIndex | RightChildIndex ]
[ 0     | 0      | 0           | 0              | 0               ]
[ 1     | 2      | 6           | 0              | 0               ]
[ 2     | 4      | 8           | 0              | 0               ]
[ 3     | 2      | 6           | 0              | 0               ]
[ 4     | 3      | 7           | 0              | 0               ]
[ 5     | 3      | 7           | 0              | 0               ]
[ 6     | 4      | 8           | 1              | 3               ]
[ 7     | 6      | 9           | 4              | 5               ]
[ 8     | 8      | 9           | 6              | 2               ]
[ 9     | 14     | 0           | 7              | 8               ]
2023-3--[Info]--Create HaffmanCode     : OK
2023-3--[Info]--HaffmanCode            :
[ Index | Code    ]
[ 1     | 100     ]
[ 2     | 11      ]
[ 3     | 101     ]
[ 4     | 00      ]
[ 5     | 01      ]
2023-3--[Info]--Destory HaffmanCode    : OK
2023-3--[Info]--Destory HaffmanTree    : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK

查看全文

http://www.kler.cn/a/3944.html