最小生成树应用北极通讯网络

题目 2396: 

信息学奥赛一本通T1487-北极通讯网络

时间限制: 2s 内存限制: 192MB 提交: 37 解决: 14

题目描述

原题来自：Waterloo University 2002

北极的某区域共有 n 座村庄，每座村庄的坐标用一对整数 (x,y) 表示。为了加强联系，决定在村庄之间建立通讯网络。通讯工具可以是无线电收发机，也可以是卫星设备。所有的村庄都可以拥有一部无线电收发机， 且所有的无线电收发机型号相同。但卫星设备数量有限，只能给一部分村庄配备卫星设备。

不同型号的无线电收发机有一个不同的参数 d，两座村庄之间的距离如果不超过 d 就可以用该型号的无线电收发机直接通讯，d 值越大的型号价格越贵。拥有卫星设备的两座村庄无论相距多远都可以直接通讯。

现在有 k 台卫星设备，请你编一个程序，计算出应该如何分配这 k 台卫星设备，才能使所拥有的无线电收发机的 d 值最小，并保证每两座村庄之间都可以直接或间接地通讯。

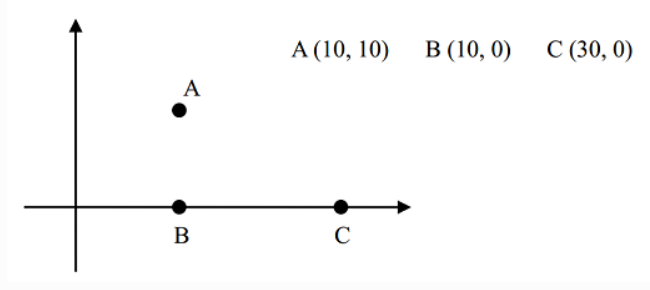
例如，对于下面三座村庄：

其中 |AB|=10,|BC|=20,|AC|=10–√5≈22.36

如果没有任何卫星设备或只有 1 台卫星设备 (k=0或 k=1)，则满足条件的最小的 d=20，因为 A和 B，B和 C 可以用无线电直接通讯；而 A 和 C可以用 B 中转实现间接通讯 (即消息从 A 传到 B，再从 B 传到 C)；

如果有 2 台卫星设备 (k=2），则可以把这两台设备分别分配给 B 和 C ，这样最小的 d 可取 10，因为 A 和 B 之间可以用无线电直接通讯；B 和 C 之间可以用卫星直接通讯；A 和 C 可以用 B 中转实现间接通讯。

如果有 3 台卫星设备，则 A,B,C 两两之间都可以直接用卫星通讯，最小的 d 可取 0。

输入格式

第一行为由空格隔开的两个整数 n,k;
第 2∼n+1行，每行两个整数，第 i 行的 xi,yi表示第 i 座村庄的坐标 (xi,yi)。

输出格式

一个实数，表示最小的 d 值，结果保留 2 位小数。

样例输入

复制

3 2
10 10
10 0
30 0

样例输出

复制

10.00

提示

数据范围:

对于全部数据，1≤n≤500,0≤x,y≤104,0≤k≤100。

 思路：

这题算是最小生成树中最简单的应用了，只需要考虑提前结束建树，和记录最长树边。

#include<bits/stdc++.h>
using namespace std;
const int N = 510, M = N * N;
int p[N];
int dx[N];
int dy[N];
struct edge {
	int a, b;
	double w;
	bool operator<(edge& W) {
		return w < W.w;
	}
}e[M];
int n, k;
double ans;
int find(int x) {
	if (x != p[x]) {
		p[x] = find(p[x]);
	}
	return p[x];
}

int main()
{
	cin >> n >> k;
	for (int i = 1;i <= n;i++) {
		cin >> dx[i] >> dy[i];
	}
	int cnt = 0;
	for (int i = 1;i <= n;i++) {
		for (int j = 1;j <= n;j++) {
			if (i == j) {
				continue;
			}
			double c = sqrt((dx[i] - dx[j]) * (dx[i] - dx[j]) + (dy[i] - dy[j]) * (dy[i] - dy[j]));
			cnt++;
			e[cnt].a = i;
			e[cnt].b = j;
			e[cnt].w = c;
		}
	}
	for (int i = 1;i <= n;i++) {
		p[i] = i;
	}
	sort(e + 1, e + 1 + cnt);
	int idx = 0;
	for (int i = 1;i <= cnt;i++) {
		if (idx == n - k ) {
			break;
		}
		int a = e[i].a;
		int b = e[i].b;
		int x = find(a);
		int y = find(b);
		if (x != y) {
			idx++;
			p[x] = y;
			ans = e[i].w;
		}
	}
	cout << fixed << setprecision(2) << ans;
}