✅DAY30 贪心算法 | 452. 用最少数量的箭引爆气球 | 435. 无重叠区间 | 763.划分字母区间
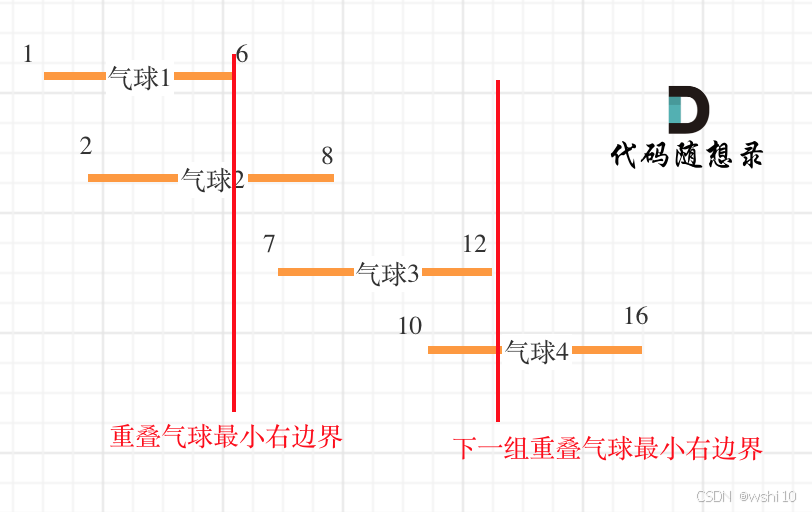
452. 用最少数量的箭引爆气球
解题思路:首先把原数组按左边界进行排序。然后比较[i-1]的右边界和[i]的左边界是否重叠,如果重叠,更新当前右边界为最小右边界和[i+1]的左边界判断是重叠。
class Solution:
def findMinArrowShots(self, points: List[List[int]]) -> int:
if len(points) == 0: return 0
points.sort(key=lambda x: x[0])
result = 1
for i in range(1, len(points)):
if points[i][0] > points[i-1][1]: # 第二段的头和第一段的尾不衔接
result += 1
else:
points[i][1] = min(points[i-1][1], points[i][1])
# else是这两段重叠,但是要判断下一个部分是否重叠
# 更新尾为最小的右边界,如果下一个[i][0]< [i-1][1],则又有一段重叠
return result优化:按右边界排序的方式通常更直观,因为只需要维护一个变量 current_end 表示当前的射击位置,不需要更新区间边界,也减少了不必要的操作。
class Solution:
def findMinArrowShots(self, points: List[List[int]]) -> int:
if not points: return 0
points.sort(key=lambda x: x[1]) # 按右边界排序
result = 1
current_end = points[0][1]
for i in range(1, len(points)):
if points[i][0] > current_end:
result += 1
current_end = points[i][1]
return result435. 无重叠区间
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
if not intervals: return 0
intervals.sort(key = lambda x:x[0])
count = 0
for i in range(1, len(intervals)):
if intervals[i-1][1] > intervals[i][0]: # 存在重叠
intervals[i][1] = min(intervals[i-1][1], intervals[i][1])
count += 1
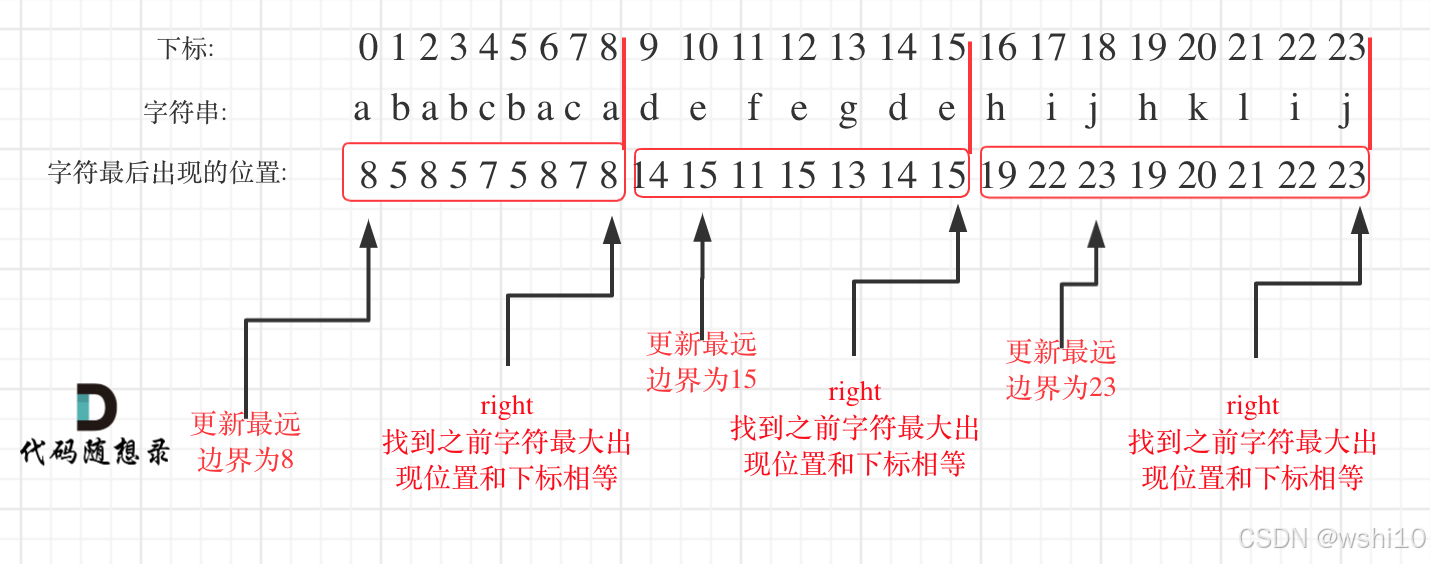
return count763. 划分字母区间
class Solution:
def partitionLabels(self, s: str) -> List[int]:
last_occ = {}
result = []
for i, char in enumerate(s):
last_occ[char] = i
start_index, end_index = 0, 0
for i, char in enumerate(s):
end_index = max(end_index, last_occ[char])#找出当前字符出现的最远位置
if i == end_index:#i遍历到当前end的最尾部,说明前面的所有出现字符到这停下了
result.append(end_index - start_index + 1)
start_index = i + 1
return result