几种常见的校验算法
目录
一、校验和
二、异或校验
三、CRC校验
四、MD5算法
五、SM3算法
六、SHA算法
UART有一个奇偶校验,CAN通信有CRC校验。Modbus、USB等通信协议也有校验信息。在自定义数据存储时,有经验的工程师一般都会添加一定校验信息。
一、校验和
校验和是最基本,也是嵌入式软件工程师最常用的一种校验算法,其实现方法很简单。
实现原理:按每个字节,计算累加和。
实现的方式方法很多,不同的编程语言,不同的应用有所不同,下面以C语言8位校验和为例:
uint8_t CheckSum(uint8_t *Buf, uint8_t Len)
{
uint8_t i = 0;
uint8_t sum = 0;
uint8_t checksum = 0;
for(i=0; i<Len; i++)
{
sum += *Buf++;
}
checksum = sum & 0xff;
return checksum;
}二、异或校验
【异或校验】与【校验和】类似,对数据进行“异或”,最终得到一个“异或值”。
实现原理:按每个字节异或,求结果。
校验和、异或校验的方式有很多种,比如有的还会传入一个参数作为异或校验的值。实现的方式方法很多,不同的编程语言,不同的应用有所不同,下面以C语言为例:
uint8_t CheckXOR(uint8_t *Buf, uint8_t Len)
{
uint8_t i = 0;
uint8_t x = 0;
for(i=0; i<Len; i++)
{
x = x^(*(Buf+i));
}
return x;
}三、CRC校验
CRC:Cyclic Redundancy Check,即循环冗余校验。
CRC是数据通信领域中最常用的一种查错校验码,其特征是信息字段和校验字段的长度可以任意选定。循环冗余检查(CRC)是一种数据传输检错功能,对数据进行多项式计算,并将得到的结果附在帧的后面,接收设备也执行类似的算法,以保证数据传输的正确性和完整性。
实现原理:设置crc值和多项式码;依次遍历每个字节,与crc值进行异或;crc值取出最低位的值,并右移一位;如果最低位值位1,则于多项式码进行异或;循环直到8位结束。
CRC校验属于冗余校验中的一种,大学学计算机相关专业的同学都应该学过CRC校验。
CRC有多种变体,比如:CRC-1、 CRC-5-USB、 CRC-8、 CRC-16、 CRC-32、 CRC-64等。其中,在嵌入式领域,CRC-16用的比较多。
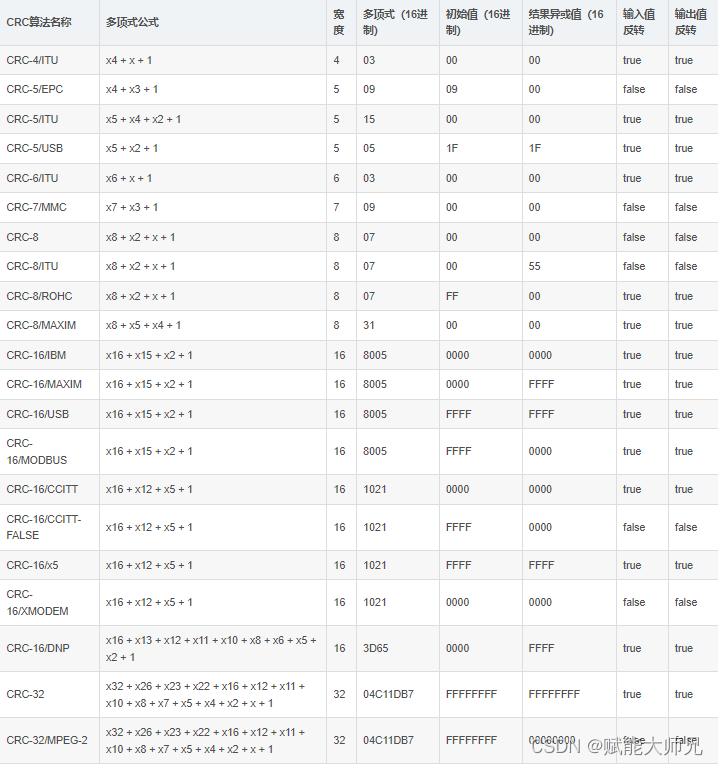
CRC校验不同场景实现方式不同,网上也有很多公开的库和源码,比如:
C语言中的开源CRC库 网上还有在线计算CRC校验值以及代码生成工具
不同的编程语言,不同的应用有所不同,下面以C语言为例:
uint16_t Crc16(uint8_t *data,uint16_t len)
{
uint16_t crc16 = 0xFFFF;
uint32_t uIndex ; //CRC查询表索引
while (len --)
{
uIndex = (crc16&0xff) ^ ((*data) & 0xff) ; //计算CRC
data = data + 1;
crc16 = ((crc16>>8) & 0xff) ^ crc16_tab[uIndex];
}
return crc16 ;//返回CRC校验值
}四、MD5算法
MD5:Message-Digest Algorithm 5,即“信息-摘要算法。消息摘要算法又称为哈希算法、散列算法,输出的消息摘要又称为哈希值、散列值。
从名字来看就知道它是从MD3、MD4发展而来的一种加密算法,其主要通过采集文件的信息摘要,以此进行计算并加密。
- 压缩性:MD5可以将任意长度的输入转化为128位长度的输出;
- 不可逆性:MD5是不可逆的,我们无法通过常规方式从MD5值倒推出它的原文;
- 抗修改性:对原文做一丁点儿改动,MD5值就会有巨大的变动,也就是说就算两个MD5值非常相似,你也不能想当然地认为它们俩对应的原文也非常相似。
实现原理:MD5是输入不定长度信息,输出固定长度128-bits的算法。经过程序流程,生成四个32位数据,最后联合起来成为一个128-bits散列。基本方式为,求余、取余、调整长度、与链接变量进行循环运算。得出结果。
因为MD5可以被暴力破解,所以MD5不再是安全的了,对安全性要求较高的场合,不建议直接使用MD5。
MD5的源码在网上都能找到现成的,而且有不同编程语言(C、 C++、 JAVA)版本。
实现对字符串和文件的MD5值的生成
五、SM3算法
随着变成技术越来越发达,校验算法也越来越多,有通用的算法,也有特殊领域特定的算法。
比如我之前开发使用由密码管理局发布的SM3密码杂凑算法。其安全性及效率与SHA-256相当。
包括SM2、SM3、SM4、SM9,杂凑值算法也可称为摘要算法或者哈希算法。实现原理:通过对数据资料的填充、分组、扩展压缩等方式计算成特定长度的数值,来作为数据指纹或者数据特征使用。
常见的MD5算法长度为128bit(16字节),SHA1算法计算长度为160bit(20字节),SHA256算法计算长度256bit(32字节),SHA512算法计算长度512bit(64字节),SM3算法计算长度为256bit(32字节)。
lk_sm3.h文件定义了一些函数宏和数据结构
#ifndef __lk_sm3_h__
#define __lk_sm3_h__
#ifdef __cpluscplus
extern "C" {
#endif
#include <strings.h>
#ifdef __cpluscplus
}
#endif
#define LK_GVALUE_LEN 64
#define LK_WORD_SIZE 32
#define LK_GVALUE_BITLEN 256
#define LK_HASH_NMEMB 8
typedef unsigned int UINT;
#ifdef i386
typedef unsigned long long UWORD;
#else
typedef unsigned long UWORD;
#endif
typedef unsigned char UCHAR;
//常量
// 0 <= j <= 15
#define LK_T0 0x79cc4519
// 16 <= j <= 63
#define LK_T1 0x7a879d8a
//循环左移
#define LOOPSHFT(a, n) ( ((a) << (n)) | ((a) >> (LK_WORD_SIZE - (n))))
//布尔函数
#define LK_FF0(x, y, z) ((x)^(y)^(z))
#define LK_FF1(x, y, z) (((x) & (y)) | ((x) & (z)) | ((y) & (z)))
#define LK_GG0(x, y, z) ((x)^(y)^(z))
#define LK_GG1(x, y, z) (( (x) & (y) ) | ((~x) & (z)))
//置换函数
#define LK_P0(x) (\
(x)^(LOOPSHFT((x), 9))^(LOOPSHFT((x), 17)) )
#define LK_P1(x) (\
(x)^(LOOPSHFT((x), 15))^(LOOPSHFT((x), 23)) )
//标准中给出的IV初始值
#define LK_INIT_VALUE(t) {\
lk_sm3_context_t *x = (t);\
x->v[0] = 0x7380166f;\
x->v[1] = 0x4914b2b9;\
x->v[2] = 0x172442d7;\
x->v[3] = 0xda8a0600;\
x->v[4] = 0xa96f30bc;\
x->v[5] = 0x163138aa;\
x->v[6] = 0xe38dee4d;\
x->v[7] = 0xb0fb0e4e;\
bzero(x->data, LK_GVALUE_LEN);\
x->total = 0;\
x->len = 0;}
#define LK_LE_ONE(t) {\
lk_sm3_context_t *x = (t);\
UINT l_z, l_d;\
for (l_z = 0; l_z < LK_HASH_NMEMB; l_z++) {\
l_d = x->v[l_z];\
x->output[l_z*4] = ((l_d >> 24) & 0x000000ff);\
x->output[l_z*4 + 1] = ((l_d >> 16) & 0x000000ff);\
x->output[l_z*4 + 2] = ((l_d >> 8) & 0x000000ff);\
x->output[l_z*4 + 3] = (l_d & 0x000000ff);\
}}
//大端转化
#define LK_GE_ONE(c) (\
((c&0x00000000000000ffUL) << 56) | (((c&0x000000000000ff00UL) << 40)) |\
((c&0x0000000000ff0000UL) << 24) | (((c&0x00000000ff000000UL) << 8)) |\
((c&0x000000ff00000000UL) >> 8) | (((c&0x0000ff0000000000UL) >> 24)) |\
((c&0x00ff000000000000UL) >> 40) | (((c&0xff00000000000000UL) >> 56)) )
#define LK_GE(w, c) \
int j2;\
for (j = 0; j <= 15; j++) {\
j2 = j*4;\
w[j] = ((c[j2] << 24) | ((c[j2+1] << 16)) |\
(c[j2+2] << 8) | (c[j2+3]));\
}
//压缩计算摘要函数
#define LK_MSG_CF(t) {\
UINT j;\
lk_sm3_context_t *x = t;\
UCHAR *data = x->data;\
UINT W1[68];\
UINT W2[64];\
UINT a,b,c,d,e,f,g,h;\
a = x->v[0];\
b = x->v[1];\
c = x->v[2];\
d = x->v[3];\
e = x->v[4];\
f = x->v[5];\
g = x->v[6];\
h = x->v[7];\
LK_GE(W1, data)\
for ( j = 16; j <= 67; j++ ) {\
W1[j] = LK_P1(W1[j-16]^W1[j-9]^(LOOPSHFT(W1[j-3], 15))) ^ LOOPSHFT(W1[j-13], 7) ^ W1[j-6];\
}\
for ( j = 0; j <= 63; j++ ) {\
W2[j] = W1[j] ^ W1[j+4];\
}\
for ( j = 0; j <= 63; j++ ) {\
UINT T, ss1, ss2, tt1, tt2;\
if ( j >= 0 && j <= 15 )\
T = LK_T0;\
else\
T = LK_T1;\
ss1 = LOOPSHFT( (LOOPSHFT(a, 12) + e + LOOPSHFT(T, j)), 7 );\
ss2 = ss1 ^ LOOPSHFT(a, 12);\
if ( j >= 0 && j <= 15 ) {\
tt1 = LK_FF0(a, b, c) + d + ss2 + W2[j];\
tt2 = LK_GG0(e, f, g) + h + ss1 + W1[j];\
} else {\
tt1 = LK_FF1(a, b, c) + d + ss2 + W2[j];\
tt2 = LK_GG1(e, f, g) + h + ss1 + W1[j];\
}\
d = c;\
c = LOOPSHFT(b, 9);\
b = a;\
a = tt1;\
h = g;\
g = LOOPSHFT(f, 19);\
f = e;\
e = LK_P0(tt2);\
}\
x->v[0] = a ^ x->v[0];\
x->v[1] = b ^ x->v[1];\
x->v[2] = c ^ x->v[2];\
x->v[3] = d ^ x->v[3];\
x->v[4] = e ^ x->v[4];\
x->v[5] = f ^ x->v[5];\
x->v[6] = g ^ x->v[6];\
x->v[7] = h ^ x->v[7];\
x->len = 0;\
}
typedef struct lk_sm3_context_s
{
UINT len;
UINT total;
UCHAR data[LK_GVALUE_LEN];
UINT v[LK_HASH_NMEMB];
UCHAR output[LK_WORD_SIZE];
} lk_sm3_context_t;
#ifdef __cpluscplus
extern "C" {
#endif
extern void lk_sm3_final(lk_sm3_context_t *context);
extern void lk_sm3_update (lk_sm3_context_t *context, UCHAR *data, UINT len);
#ifdef __cpluscplus
}
#endif
#endiflk_sm3.c文件实现了update和final两个函数
#include <stdio.h>
#include <string.h>
#include "lk_sm3.h"
static void lk_sm3_cf(lk_sm3_context_t *context)
{
LK_MSG_CF(context)
}
void lk_sm3_update (lk_sm3_context_t *context, UCHAR *data, UINT len)
{
int real_len, free, offset = 0;
real_len = len + context->len;
if (real_len < LK_GVALUE_LEN) {
//本次数据不够一个分组大小,先缓存起来
memcpy(context->data + context->len, data + offset, len);
context->len = real_len;
context->total += len;
return;
}
free = LK_GVALUE_LEN - context->len;
memcpy(context->data + context->len, data + offset, free);
context->total += free;
offset += free;
len -= free;
//进行迭代压缩
lk_sm3_cf(context);
while (1) {
if (len < LK_GVALUE_LEN) {
//本次数据不够一个分组大小,先缓存起来
memcpy(context->data + context->len, data + offset, len);
context->len = len;
context->total += len;
return;
}
memcpy(context->data + context->len, data + offset, LK_GVALUE_LEN);
offset += LK_GVALUE_LEN;
len -= LK_GVALUE_LEN;
context->total += LK_GVALUE_LEN;
//进行迭代压缩
lk_sm3_cf(context);
}
}
void lk_sm3_final(lk_sm3_context_t *context)
{
UINT tk, k, free, i, len;
UCHAR tmp[LK_GVALUE_LEN] = {0};
tk = context->total * 8 % 512;
if (tk < 448) {
k = 448 - tk;
} else {
k = 448 -tk + 512;
}
//计算需要填充的字节
k = k / 8 + 8;
free = LK_GVALUE_LEN - context->len;
k--;
context->data[context->len] = 0x80;
len = context->total * 8;
for (i = context->len + 1; i < LK_GVALUE_LEN; i++, k--) {
if (k != 8)
context->data[i] = 0x00;
else {
bzero(context->data + i, 8);
UWORD *pdata = (UWORD *)&(context->data[i]);
*pdata = LK_GE_ONE(len);
break;
}
}
//进行迭代压缩
lk_sm3_cf(context);
if (64 == k) {
for (i = 0; i < LK_GVALUE_LEN; i++, k--) {
if (k != 8)
context->data[i] = 0x00;
else {
bzero(context->data + i, 8);
UWORD *pdata = (UWORD *)&(context->data[i]);
*pdata = LK_GE_ONE(len);
break;
}
}
//进行迭代压缩
lk_sm3_cf(context);
}
//get result
LK_LE_ONE(context)
}六、SHA算法
还有从MD4算法改进而来的SHA-1算法。
SHA(Secure Hash Algorithm),安全哈希算法,包括SHA-1、SHA-256、SHA-512等。
SHA-1和MD5都是由MD4导出的,所以它们的特点、问题和应用场景基本一致。它们的区别就是SHA-1输出的长度是160位,MD5的输出是128位,2的160次方是远远超过2的128次方这个数量级的,所以SHA-1相对来说要比MD5更安全一些,但也可以被暴力破解。
SHA的源码在网上都能找到现成的,而且有不同编程语言(C、 C++、 JAVA)版本。
