[模版总结] - 树的基本算法4 -最近公共祖先 LCA

什么是最近公共祖先LCA

LCA：在一个树中，距离两个节点p,q最近可以是其本身并且同时包含这两个子节点的节点

题目连接

Leetcode 236 - LCA
Leetcode 1644 - LCA II
Leetcode 1650 - LCAIII
Leetcode 1123 - LCA of Deepest leaves

基本思路

Leetcode 236 - LCA
Leetcode 1644 - LCA II
求解LCA的基本思路就是分治法，两个节点的相对位置关系有三种情况：

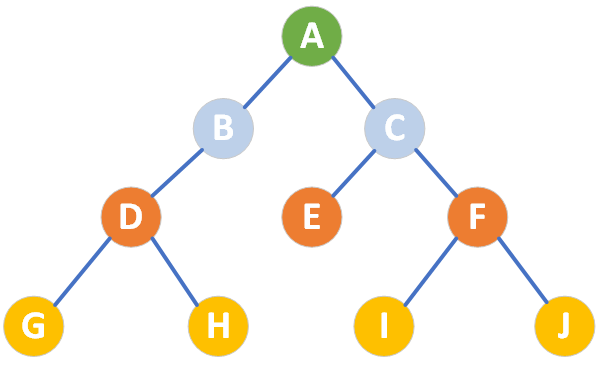
1. p和q在同一侧某个子树中，比如下图 p在H点，q在B点。
2. p和q在两侧不同子树中，比如下图p在D点，q在C点
3. 边界情况，p,q中有一个节点不存在在该树中

基于上述三种情况，分治递归过程中如果当前节点是p 或者 q那么返回该节点，如果当前节点不是p, q查看左右子树递归返回结果：

1. 如果左右有一个是p或者q或者一个非空节点(说明找到了p, q的LCA)那么返回那个点
2. 如果左右既有p又有q那么返回当前节点说明当前点就是LCA, 如果左右都是空指针那么返回空指针说明p, q和LCA都没有找到。
   解决第三种情况可以建立一个count, 遇到p和q都count++最后返回LCA时保证count==2再返回即可

代码如下

class Solution {
public:
    int count = 0;
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        auto res = dc(root, p, q);
        return count==2? res: nullptr;
    }

    TreeNode* dc(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (!root) return nullptr;

        auto l = dc(root->left, p, q);
        auto r = dc(root->right, p, q);

        if (root==p || root==q) {
            count++;
            return root; 
        } else if ((l==q && r==p) || (l==p && r==q)) return root;
        else return !l? r: l;
    }
        
};

时间复杂度：$\mathcal{O}(N)$ N代表树节点总数
空间复杂度：$\mathcal{O}(H)$ H代表树的深度，也就是栈的深度

Leetcode 1650

题目描述也是求解两个节点LCA但是树的结构中提供了parent这个节点，树有保存父节点。这道题思路就和 Leetcode 160 找到两个相交链表的相交点。p和q保证是同一个树的两个节点。

基本思路就是让p和q一直通过parent向上层移动，如果p到了root就把p指向q继续移动，如果q到了root就把q指向p继续移动，p和q最后一定会相交在相交点位置，返回这个点就是LCA

为什么一定会相交在相交点LCA位置？

• 假设p到LCA的距离是 x, q到LCA的距离为y, LCA到root的距离为z
• 根据上面的思路，p总共移动距离 x+z+y ; q总共移动距离 y+z+x 移动距离相等并在LCA处相交

代码如下

class Solution {
public:
    Node* lowestCommonAncestor(Node* p, Node * q) {
        /*
        [1,2,3,null,4]
           1
          2  3
           4    
        和找两个链表的第一个相交点类似
        // 第一种左右两边
        p -> 1 -> 2 ->3 
                        ->4 ->5->6
                  q ->7
        a + c + b 
        b + c + a
        
        // 第二种没到终点前找到另一个就返回另一个
        p -> 2-> q
        p = 2, q = 4
        p = 1, q = 2
        a + b 
        b + a      
        */
        auto pp = p;
        auto qq = q;
        while (p && q) {
            if (q==p) return q;
            q = q->parent;
            p = p->parent;
            // 如果p或者q就是LCA，那么移动p,q时后面的点一定会走到前面的点，直接返回这个点即可
            if (q==pp || p==qq) return q==pp? pp: qq;
            //到root了，回到另一个点pp或着qq继续走直到相遇
            if (!q) q=pp; 
            if (!p) p=qq;
        }
        return nullptr;
    }
};

时间复杂度：通常 $\mathcal{O}(X+Y+Z)$ x指p到LCA经过节点数，y指q到LCA经过节点数, z指LCA到root经过节点数
空间复杂度：$\mathcal{O}(1)$

Leetcode 1123

题目描述给一个二叉树找到他的所有最深的叶子节点LCA。和之前题目不同的是，这道题最深的叶子节点可能有不止两个，而且你还需要找到最深的叶子节点。
求解LCA的基本思路还是一样，不同的地方在于要在返回节点给上一层递归时，返回深度信息进行打擂台

1. 如果左右子树返回结果都不为空，判断结果深度是否相等？相等那就返回当前节点LCA, 如果不同就返回深度更深的那个结果
2. 如果左右子树返回结果一个为空一个不为空，那就返回不为空的结果即可

代码如下

class Solution {
public:
    int h = 0;
    TreeNode* lcaDeepestLeaves(TreeNode* root) {
        // dfs找到所有的deepest leaf 然后第二次给这个list的节点找LCA,由于
        auto res = dc(root, 0);
        return res.first;
    }

    pair<TreeNode*, int> dc(TreeNode* root, int h) {
        if (!root) return {root, -1};
        if (!root->left && !root->right) return {root, h};

        auto l = dc(root->left, h+1);
        auto r = dc(root->right, h+1);

        // 如果两边返回的leaf同深度，返回当前节点和该深度
        // 如果两边返回的leaf不同深度，返回深的那个
        if (l.second==-1 || r.second==-1) return l.second==-1? r: l;
        else if (l.second==r.second) return {root, l.second};
        else return l.second>r.second? l: r;
    }
};

时间复杂度：$\mathcal{O}(N)$ N为节点个数
空间复杂度：$\mathcal{O}(H)$ H为递归深度