【深度学习之回归预测篇】 深度极限学习机DELM多特征回归拟合预测(Matlab源代码)
深度极限学习机 (DELM) 作为一种新型的深度学习算法,凭借其独特的结构和训练方式,在诸多领域展现出优异的性能。本文将重点探讨DELM在多输入单输出 (MISO) 场景下的应用,深入分析其算法原理、性能特点以及未来发展前景。
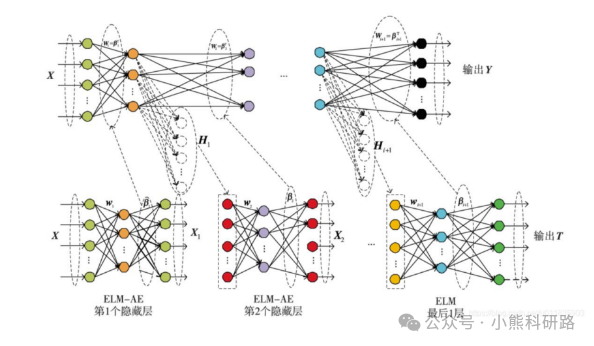
1、 DELM算法原理及其MISO拓展
极限学习机 (ELM) 作为一种单隐层前馈神经网络 (SLFN),以其快速训练速度和良好的泛化性能而备受关注。然而,传统的ELM在处理复杂非线性问题时,单隐层的表达能力有限。DELM则通过堆叠多个ELM层,构建深度结构,有效提升了网络的表达能力和学习能力。
在MISO场景下,DELM的输入层接收多个输入变量,经过多个ELM层的逐层非线性变换,最终输出单个标量值。每一层ELM都包含输入权重矩阵、偏置向量和激活函数。与传统深度学习算法不同的是,DELM的每一层ELM的权重和偏置都是随机生成的,无需迭代调整。只有输出层的权重需要通过最小二乘法或其他优化算法进行学习。这种独特的训练方式极大地缩短了训练时间,避免了容易陷入局部最优解的风险。
具体来说,假设DELM包含L层ELM,输入向量为𝑥∈𝑅𝑛x∈Rn,输出为𝑦∈𝑅y∈R。第l层ELM的输出为ℎ𝑙=𝑔𝑙(𝑊𝑙𝑥𝑙+𝑏𝑙)hl=gl(Wlxl+bl),其中𝑊𝑙Wl是输入权重矩阵,𝑏𝑙bl是偏置向量,𝑔𝑙gl是激活函数,𝑥𝑙xl是第l层的输入向量 (第一层输入为𝑥x,后续层输入为前一层输出)。最后一层ELM的输出ℎ𝐿hL通过线性组合得到最终输出:𝑦=𝛽𝑇ℎ𝐿y=βThL,其中𝛽β是输出权重向量。
2、 DELM MISO的性能分析
DELM MISO模型的性能受到多个因素的影响,包括:
网络层数 (L): 层数的增加可以提高网络的表达能力,但同时也会增加计算复杂度和过拟合的风险。需要根据实际问题选择合适的层数。
隐层神经元个数 (N): 隐层神经元个数决定了网络的复杂度,过少则可能导致欠拟合,过多则可能导致过拟合。合适的个数需要通过交叉验证等方法确定。
激活函数的选择: 激活函数的选择对网络的学习能力和泛化性能有重要影响。常用的激活函数包括sigmoid函数、ReLU函数等。不同激活函数适用于不同类型的数据和问题。
输入数据的预处理: 输入数据的归一化、标准化等预处理步骤可以提高模型的训练效率和预测精度。
相比于传统的深度学习算法,DELM MISO在训练速度方面具有显著优势。由于其权重不需要迭代更新,训练时间大大缩短,尤其在处理大规模数据集时,这种优势更加明显。同时,DELM MISO的泛化性能也相对较好,能够有效避免过拟合问题。然而,DELM MISO也存在一些不足,例如参数选择较为依赖经验,对噪声敏感性较高。
3、运行效果展示
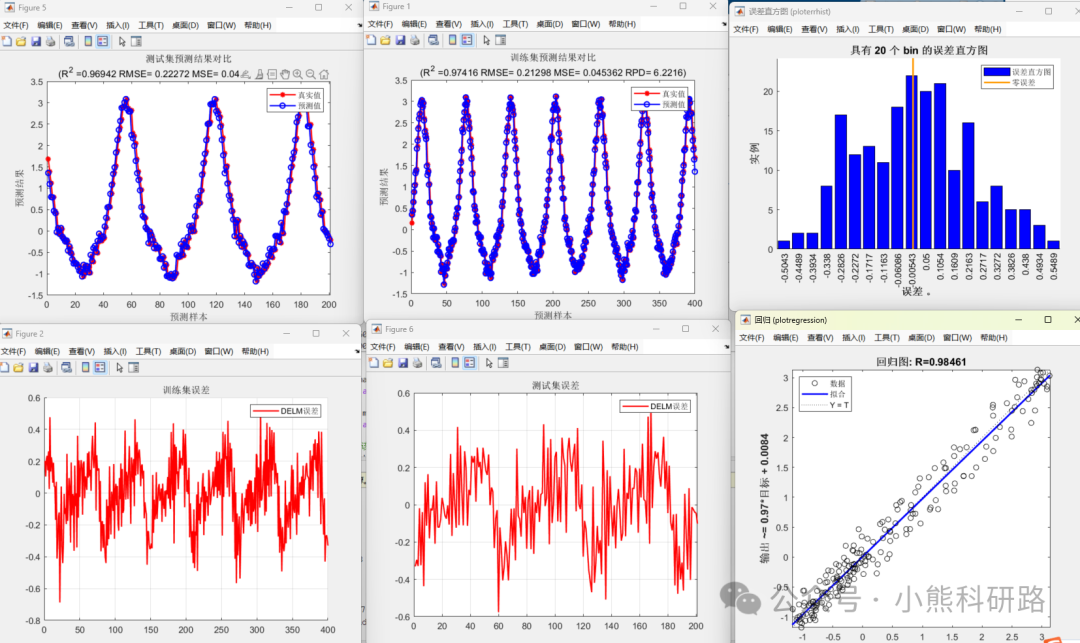
本文采用Matlab编写了深度学习之深度极限学习机 (DELM)回归预测模型代码,代码注释详细,编写逻辑清晰易懂,可一键运行,数据集采用excel数据形式,方便替换数据集。适合新手学习和SCI建模使用。
评价指标全面包括 MAE,MAPE,MSE,RMSE,R2,error,errorPercent,RPD等性能指标,出图包括训练集和预测集预测对比图果,拟合效果图,误差直方图、相对误差图等进行可视化分析,使用起来简单方便,直接替换成自己的数据即可生成美观图形用于写作。
