当前位置：首页 > article >正文

【基础算法】1-2：归并排序

article 2025/1/16 3:00:08

归并排序

OVERVIEW

归并排序
- - 1.归并排序
  - - （1）基本思想
    - （2）归并排序特性
  - 2.归并排序模板
  - 3.归并排序练习
  - - （1）AcWing787.归并排序
    - （2）AcWing788.逆序对的数量

1.归并排序

（1）基本思想

确定分界点mid = (low + high) / 2
先对左边进行归并排序，然后对右边进行归并排序
将两个有序子序列归并为一个有序序列

（2）归并排序特性

归并排序时间效率为O（nlog₂n）
归并排序空间效率为O（n）
归并排序是一个稳定的排序算法

注：关于2路归并的归并树（倒立的二叉树）

二叉树的第h层最多有2^h-1个结点，即满足 n ≤ 2^h-1 即为 h - 1 = $\lceil log_2n \rceil$
n个元素进行2路归并，归并趟数为 $\lceil log_2n \rceil$

2.归并排序模板

//写法1:for循环写法
//[low...mid]和[mid+1...high]各自有序 将两个部分归并
void merge(int A[], int n, int low, int mid, int high) {//需要传入数组大小n以节省不必要的空间浪费
    int i, j, k;
    int *B = (int *)malloc(n * sizeof(int));//辅助数组B
    for (k = low; k <= high; ++k) B[k] = A[k];
    for (i = low, j = mid + 1, k = i; i <= mid && j <= high; ++k) {//核心归并操作
        if (B[i] <= B[j]) A[k] = B[i++];
        else A[k] = B[j++];
    }
    while(i <= mid) A[k++] = B[i++];//未归并完的部分直接复制到尾部
    while(j <= high) A[k++] = B[j++];
}

void mergeSort(int A[], int n, int low, int high) {
    if (low < high) {
        int mid = (low + high)/2;//从中间划分
        mergeSort(A, n, low, mid);//左半部分归并排序
        mergeSort(A, n, mid + 1, high);//右半部分归并排序
        merge(A, n, low, mid, high);//归并操作
    }
}

//写法2:while循环写法
void my_merge_sort(int arrA[], int low, int high) {
    if (low >= high) return;
    int mid = (low + high) / 2;
    my_merge_sort(arrA, low, mid);
    my_merge_sort(arrA, mid + 1, high);
    
    int i = low, j = mid + 1, k = 0;
    while (i <= mid && j <= high) {
        if (arrA[i] <= arrA[j]) arrB[k++] = arrA[i++];
    	else arrB[k++] = arrA[j++];
    }
    while (i <= mid) arrB[k++] = arrA[i++];
    while (j <= high) arrB[k++] = arrA[j++];
    for (i = low, j = 0; i <= high; i++, j++) arrA[i] = arrB[j];//将数组数据拷贝回arrA
}

3.归并排序练习

（1）AcWing787.归并排序

（2）AcWing788.逆序对的数量

逆序对的定义：

对于数列的第 i 个和第 j 个元素，如果满足 i < j 且 a[i] > a[j]，则其为一个逆序对。

分治法解决，将序列从中间分开，将逆序对分成三类：

两个元素都在左边；
两个元素都在右边；
两个元素一个在左一个在右；

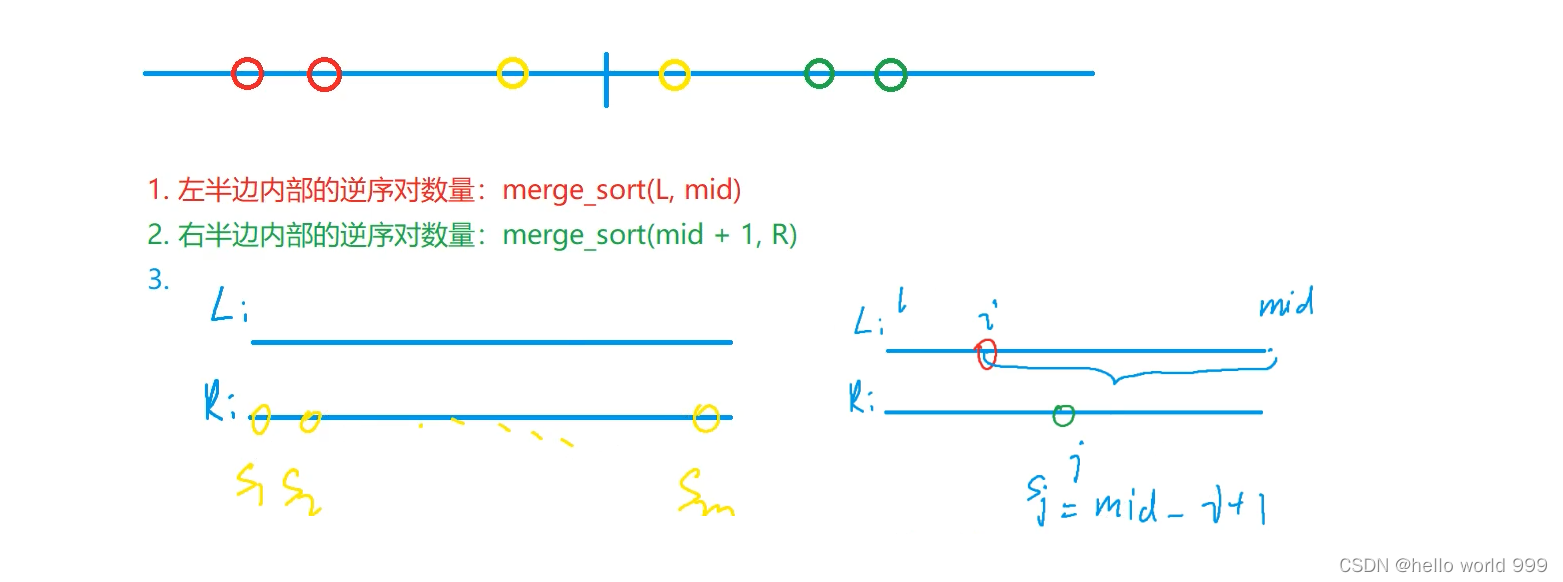
这个时候我们注意到一个很重要的性质，左右半边的元素在各自任意调换顺序，是不影响第三步计数的。因此我们可以数完就给它排序，这么做的好处在于，如果序列是有序的会让第三步计数很容易。如果无序暴力数的话这一步是O(n^2)的。

比如序列是这样的 4 5 6 | 1 2 3

当你发现 4 比 3 大的时候，也就是说右边最大的元素都小于左边最小的元素，那么左边剩下的5和6都必然比右边的所有元素大，因此就可以不用数5和6的情形了，直接分别加上右半边的元素个数就可以了，这一步就降低到了O(n), 我们知道递归式 T(n) = 2T(n/2)+O(n) = O(nlogn)的，所以排序的成本是可以接受的，并且这一问题下，可以很自然地使用归并排序。

#include<iostream>
using namespace std;

const int MAX = 1e6 + 10;

int n, arrA[MAX], arrB[MAX];

long long my_merge_sort(int low, int high) {
    if (low >= high) return 0;
    int mid = (low + high) / 2;
    long long res = my_merge_sort(low, mid) + my_merge_sort(mid + 1, high);

    int i = low, j = mid + 1, k = 0;
    while (i <= mid && j <= high) {
        if (arrA[i] <= arrA[j]) {
            arrB[k++] = arrA[i++];
        } else {//arrA[i] > arrA[j]满足逆序数的定义
            arrB[k++] = arrA[j++];
            res += (mid - i + 1);
        }
    }
    while (i <= mid) arrB[k++] = arrA[i++];
    while (j <= high) arrB[k++] = arrA[j++];
    for (int i = low, j = 0; i <= high; ++i, ++j) arrA[i] = arrB[j];
    return res;
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) scanf("%d", &arrA[i]);
    cout << my_merge_sort(0, n - 1) << endl;
    return 0;
}