机器学习头歌（第三部分-强化学习）

一、强化学习及其关键元素

二、强化学习的分类

三、任务与奖赏

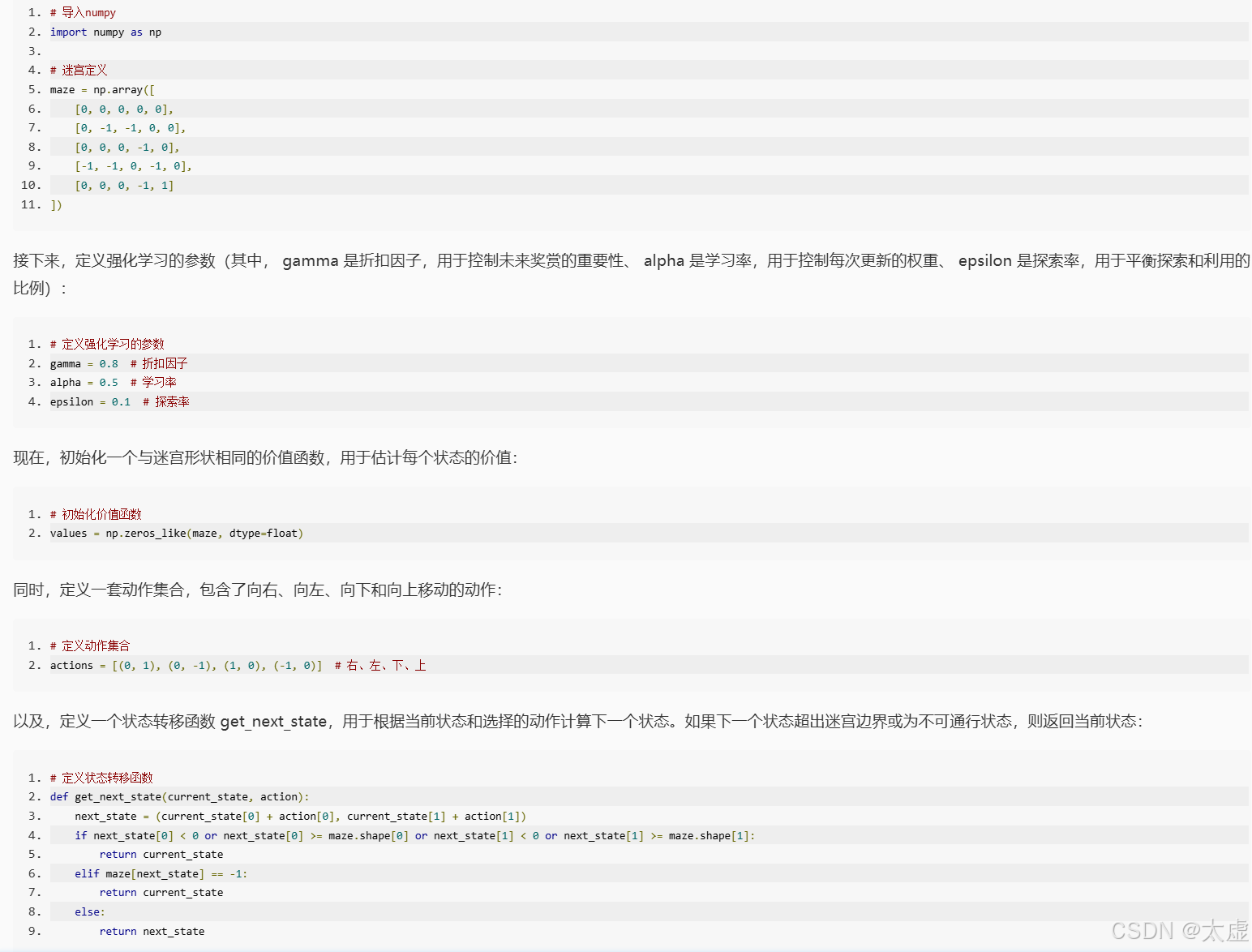
import numpy as np

# 迷宫定义
maze = np.array([
    [0, 0, 0, 0, 0],
    [0, -1, -1, 0, 0],
    [0, 0, 0, -1, 0],
    [-1, -1, 0, -1, 0],
    [0, 0, 0, -1, 1]
])

# 定义强化学习的参数
gamma = 0.8  # 折扣因子
alpha = 0.5  # 学习率
epsilon = 0.1  # 探索率

# 初始化价值函数
values = np.zeros_like(maze, dtype=float)

# 定义动作集合
actions = [(0, 1), (0, -1), (1, 0), (-1, 0)]  # 右、左、下、上

# 定义状态转移函数
def get_next_state(current_state, action):
    next_state = (current_state[0] + action[0], current_state[1] + action[1])
    if next_state[0] < 0 or next_state[0] >= maze.shape[0] or next_state[1] < 0 or next_state[1] >= maze.shape[1]:
        return current_state
    elif maze[next_state] == -1:
        return current_state
    else:
        return next_state

# 进行强化学习训练
num = 0
for _ in range(10):

    # 请在下面的 Begin-End 之间按照注释中给出的提示编写正确的代码
    ########## Begin ##########
    state = (0, 0)  # 初始状态
    while state != (4, 4):  # 未到达目标状态时
        if np.random.rand() < epsilon:  # 探索
            action = actions[np.random.randint(len(actions))]
        else:  # 利用
            action_values = []
            for a in actions:
                next_state = get_next_state(state, a)
                action_values.append(values[next_state])
            max_value = np.max(action_values)
            max_indices = [i for i, v in enumerate(action_values) if v == max_value]
            action_index = np.random.choice(max_indices)
            action = actions[action_index]
        next_state = get_next_state(state, action)
        reward = maze[next_state]
        values[state] += alpha * (reward + gamma * values[next_state] - values[state])
        state = next_state


    ########## End ##########

        next_state = get_next_state(state, action)
        reward = maze[next_state]
        values[state] += alpha * (reward + gamma * values[next_state] - values[state])
        state = next_state
    num = num + 1

四、K-摇臂赌博机

1.探索与利用

import numpy as np

# 请在下面的 Begin-End 之间按照注释中给出的提示编写正确的代码
########## Begin ##########

# 定义k-摇臂赌博机类
# 定义k-摇臂赌博机类
class Bandit:
    def __init__(self, k):
        self.k = k
        self.q_star = np.random.normal(0, 1, k)  # 真实回报分布
    # 选择拉杆并获得奖励
    def pull(self, action):
        reward = np.random.normal(self.q_star[action], 1)
        return reward

# 选择摇臂
actions=6

# 第六步：创建一个 10-摇臂赌博机实例
bandit = Bandit(k=10)

# 第七步：完成一次摇臂选择和奖励获取
reward = bandit.pull(actions)

# 选择摇臂
actions=6

########## End ##########

2.ϵ -贪心

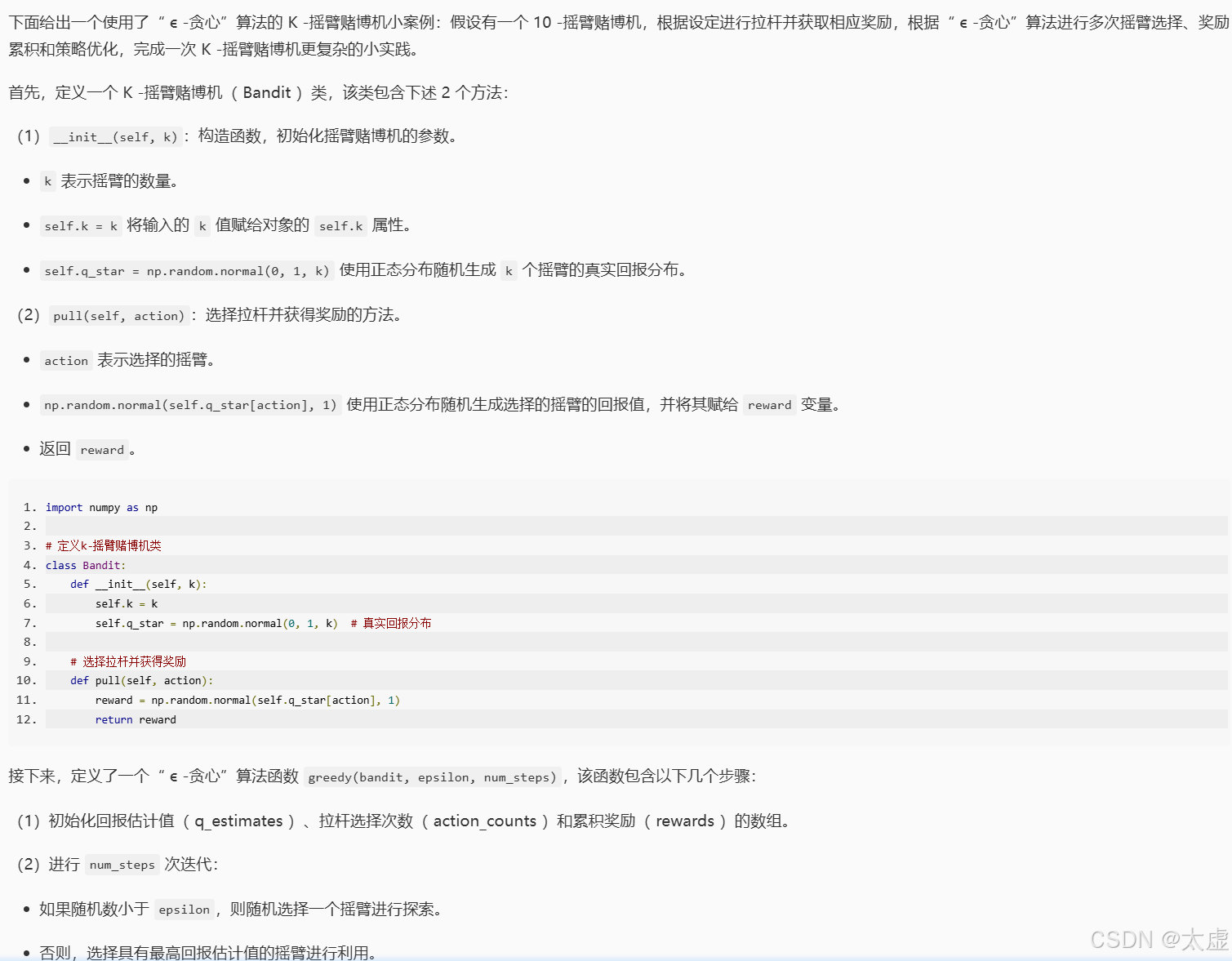
import numpy as np

# 定义k-摇臂赌博机类
class Bandit:
    def __init__(self, k):
        self.k = k
        self.q_star = np.random.normal(0, 1, k)  # 真实回报分布

    # 选择拉杆并获得奖励
    def pull(self, action):
        reward = np.random.normal(self.q_star[action], 1)
        return reward

# 请在下面的 Begin-End 之间按照注释中给出的提示编写正确的代码
########## Begin ##########

# 贪心算法
def greedy(bandit, epsilon, num_steps):
    q_estimates = np.zeros(bandit.k)  # 回报估计值
    action_counts = np.zeros(bandit.k)  # 拉杆选择次数
    rewards = np.zeros(num_steps)  # 累积奖励
    for step in range(num_steps):
        if np.random.random() < epsilon:
            # 随机选择拉杆进行探索
            action = np.random.randint(0, bandit.k)
        else:
            # 选择具有最高回报估计值的拉杆进行利用
            action = np.argmax(q_estimates)
        reward = bandit.pull(action)
        action_counts[action] += 1
        q_estimates[action] += (reward - q_estimates[action]) / action_counts[action]
        rewards[step] = reward
    return rewards
########## End ##########

# 创建一个k-摇臂赌博机实例
bandit = Bandit(k=10)

# 使用贪心算法进行探索与利用
epsilon = 0.1
num_steps = 10
rewards_greedy = greedy(bandit, epsilon, num_steps)

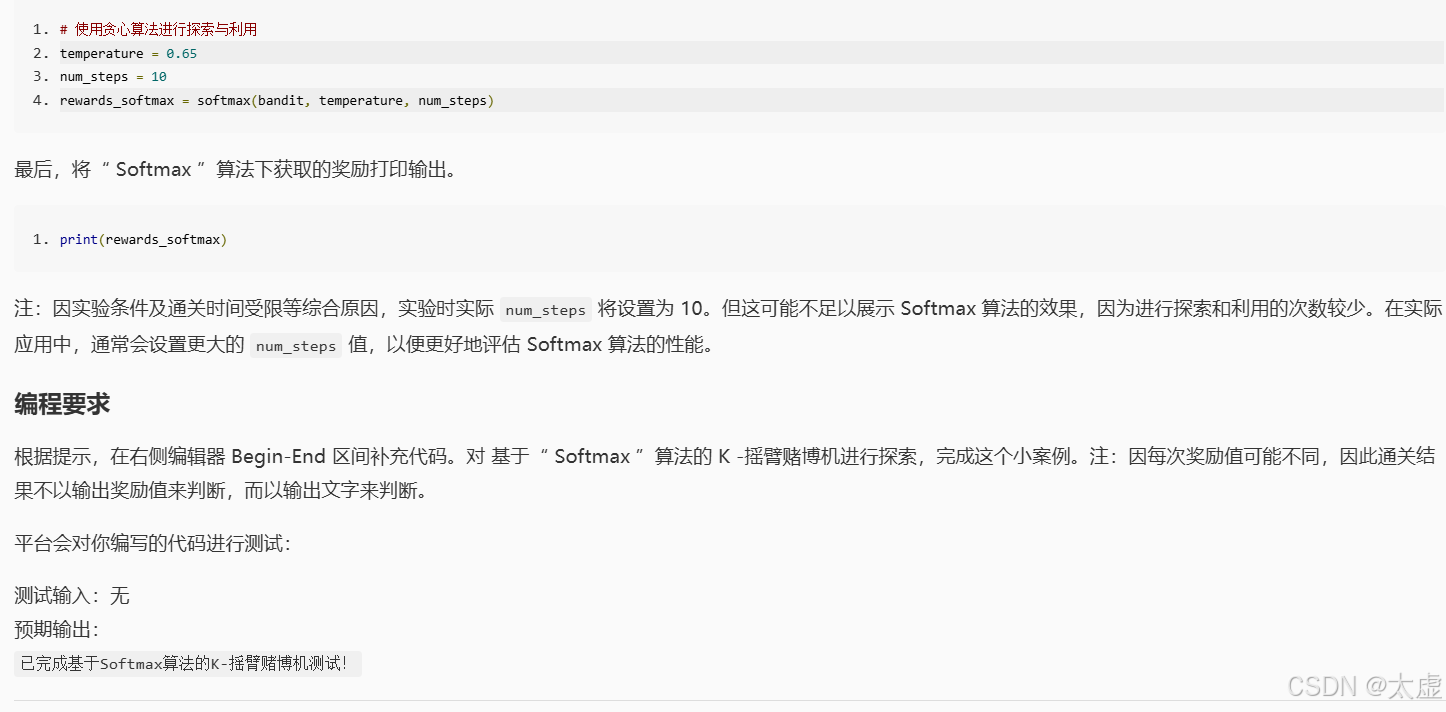
3.Softmax

import numpy as np

# 定义k-摇臂赌博机类
class Bandit:
    def __init__(self, k):
        self.k = k
        self.q_star = np.random.normal(0, 1, k)  # 真实回报分布

    # 选择拉杆并获得奖励
    def pull(self, action):
        reward = np.random.normal(self.q_star[action], 1)
        return reward

# 请在下面的 Begin-End 之间按照注释中给出的提示编写正确的代码
########## Begin ##########

# Softmax算法
def softmax(bandit, temperature, num_steps):
    action_preferences = np.zeros(bandit.k)  # 拉杆的偏好值
    rewards = np.zeros(num_steps)  # 累积奖励
    for step in range(num_steps):
        action_probs = np.exp(action_preferences / temperature) / np.sum(np.exp(action_preferences / temperature))
        action = np.random.choice(range(bandit.k), p=action_probs)
        reward = bandit.pull(action)
        action_preferences[action] += reward
        rewards[step] = reward
    return rewards

########## End ##########

# 创建一个k-摇臂赌博机实例
bandit = Bandit(k=10)

# 使用Softmax算法进行探索与利用
temperature = 0.65
num_steps = 10
rewards_softmax = softmax(bandit, temperature, num_steps)

五、有模型学习

1.策略评估

2.策略改进

import numpy as np

# 定义一个简单的环境类
class Environment:
    def __init__(self):
        self.num_states = 3
        self.num_actions = 2
        self.transition_matrix = np.array([
            [[0.6, 0.2, 0.2], [0.2, 0.6, 0.2], [0.4, 0.4, 0.2]],  # 状态0对应的两个动作的转移概率
            [[0.3, 0.3, 0.4], [0.4, 0.3, 0.3], [0.9, 0.05, 0.05]],  # 状态1对应的两个动作的转移概率
            [[0.1, 0.3, 0.6], [0.5, 0.2, 0.3], [0.1, 0.4, 0.5]]   # 状态2对应的两个动作的转移概率
        ])
        self.reward_matrix = np.array([
            [1, -1, 0],  # 状态0对应的两个动作的奖励
            [-1, 1, 0],  # 状态1对应的两个动作的奖励
            [0, 0, 1]    # 状态2对应的两个动作的奖励
        ])

    def step(self, state, action):
        next_state = np.random.choice(range(self.num_states), p=self.transition_matrix[state][action])
        reward = self.reward_matrix[state][action]
        return next_state, reward

# 策略评估算法
def policy_evaluation(env, policy, gamma, theta, num_iterations):
    V = np.zeros(env.num_states)  # 初始化状态价值函数
    for i in range(num_iterations):
        delta = 0
        for s in range(env.num_states):
            v = V[s]
            q_values = np.zeros(env.num_actions)
            for a in range(env.num_actions):
                for s_next in range(env.num_states):
                    p = env.transition_matrix[s][a][s_next]
                    r = env.reward_matrix[s][a]
                    q_values[a] += p * (r + gamma * V[s_next])
            V[s] = np.sum(policy[s] * q_values)
            delta = max(delta, abs(v - V[s]))
        if delta < theta:
            break
    return V

# 请在下面的 Begin-End 之间按照注释中给出的提示编写正确的代码
########## Begin ##########

# 策略改进算法
# 策略改进算法
def policy_improvement(env, policy, gamma, theta, num_iterations):
    while True:
        V = policy_evaluation(env, policy, gamma, theta, num_iterations)
        policy_stable = True
        for s in range(env.num_states):
            old_action = np.argmax(policy[s])  # 记录旧的行动
            q_values = np.zeros(env.num_actions)
            for a in range(env.num_actions):
                for s_next in range(env.num_states):
                    p = env.transition_matrix[s][a][s_next]
                    r = env.reward_matrix[s][a]
                    q_values[a] += p * (r + gamma * V[s_next])
            best_action = np.argmax(q_values)  # 寻找最优行动
            policy[s] = np.eye(env.num_actions)[best_action]
            if old_action != best_action:
                policy_stable = False
        if policy_stable:
            break
    return V

########## End ##########

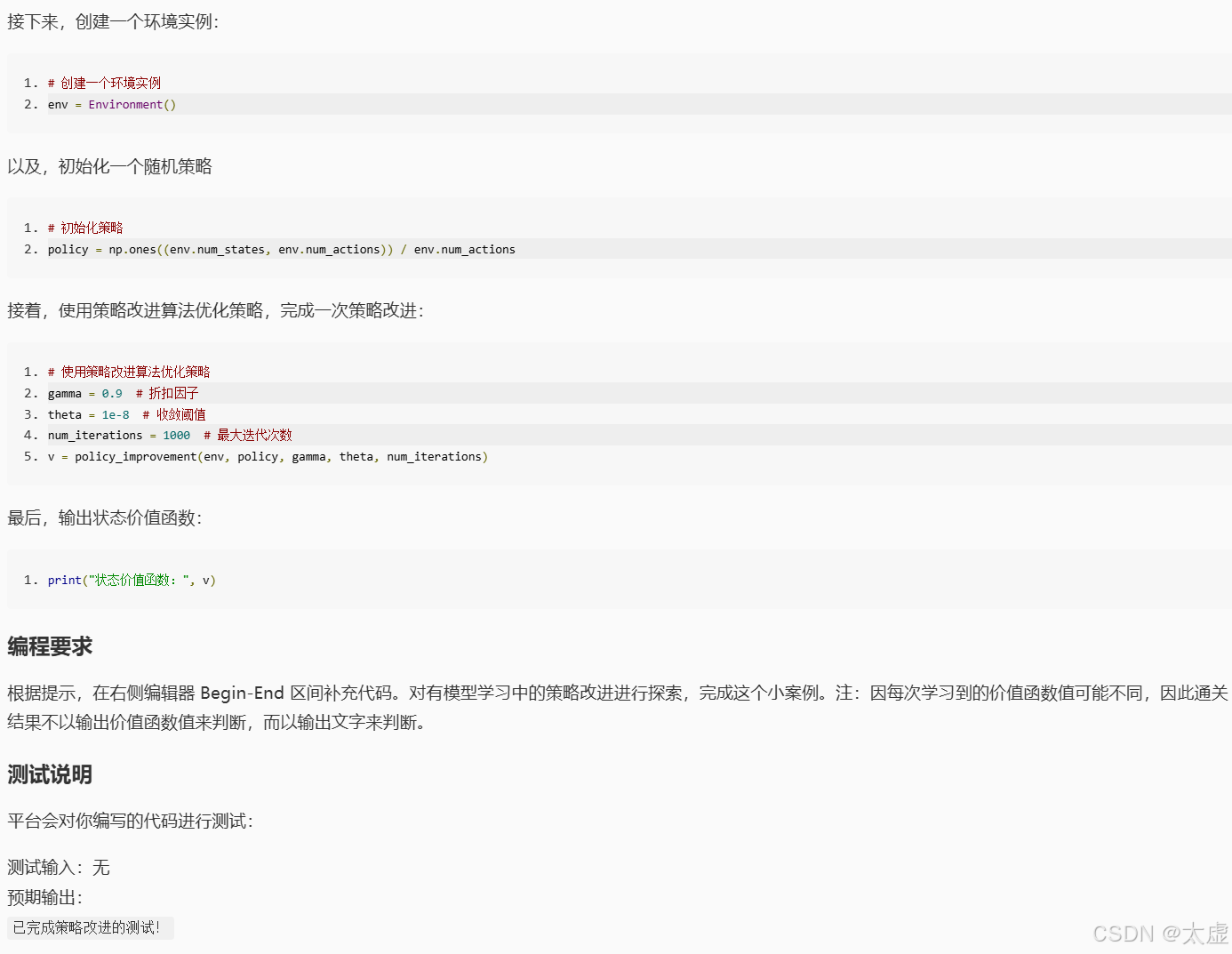
# 创建一个环境实例
env = Environment()

# 初始化一个随机策略
policy = np.ones((env.num_states, env.num_actions)) / env.num_actions

# 使用策略改进算法优化策略
gamma = 0.9  # 折扣因子
theta = 1e-8  # 收敛阈值
num_iterations = 1000  # 最大迭代次数
v = policy_improvement(env, policy, gamma, theta, num_iterations)


 

3.策略迭代与值迭代

import gym
import numpy as np

def policy_evaluation(env, policy, gamma=0.9, threshold=1e-6):
    num_states = env.observation_space.n
    num_actions = env.action_space.n

    # 初始化值函数
    values = np.zeros(num_states)

    while True:
        delta = 0

        for state in range(num_states):
            v = values[state]

            # 根据贝尔曼方程更新值函数
            q_values = np.zeros(num_actions)
            for action in range(num_actions):
                for prob, next_state, reward, _ in env.P[state][action]:
                    q_values[action] += prob * (reward + gamma * values[next_state])

            # 更新值函数
            values[state] = np.sum(policy[state] * q_values)

            delta = max(delta, np.abs(v - values[state]))

        if delta < threshold:
            break

    return values

# 请在下面的 Begin-End 之间按照注释中给出的提示编写正确的代码
########## Begin ##########

def policy_iteration(env, gamma=0.9, max_iterations=10000):
    num_states = env.observation_space.n
    num_actions = env.action_space.n
    # 初始化策略函数
    policy = np.ones((num_states, num_actions)) / num_actions
    for _ in range(max_iterations):
        # 策略评估
        values = policy_evaluation(env, policy, gamma)
        policy_stable = True
        for state in range(num_states):
            old_action = np.argmax(policy[state])
            # 策略改进
            q_values = np.zeros(num_actions)
            for action in range(num_actions):
                for prob, next_state, reward, _ in env.P[state][action]:
                    q_values[action] += prob * (reward + gamma * values[next_state])
            new_action = np.argmax(q_values)
            if old_action != new_action:
                policy_stable = False
            policy[state] = np.eye(num_actions)[new_action]
        if policy_stable:
            break
    return policy


def value_iteration(env, gamma=0.9, max_iterations=10000):
    num_states = env.observation_space.n
    num_actions = env.action_space.n

    # 初始化值函数
    values = np.zeros(num_states)

    for _ in range(max_iterations):
        delta = 0

        for state in range(num_states):

            # 第六步：记录当前状态的旧值


            # 更新值函数
            q_values = np.zeros(num_actions)
            for action in range(num_actions):
                for prob, next_state, reward, _ in env.P[state][action]:
                    q_values[action] += prob * (reward + gamma * values[next_state])

            # 第七步：使用Q值的最大值更新值函数


            # 第八步：计算值函数的变化量


        if delta < 1e-6:
            break

    # 根据最终的值函数，生成最优策略
    policy = np.zeros((num_states, num_actions))
    for state in range(num_states):
        q_values = np.zeros(num_actions)
        for action in range(num_actions):
            for prob, next_state, reward, _ in env.P[state][action]:
                q_values[action] += prob * (reward + gamma * values[next_state])
        best_action = np.argmax(q_values)
        policy[state][best_action] = 1.0
    return values

########## End ##########

env = gym.make('FrozenLake-v0')

# 使用策略迭代
v1 = policy_iteration(env)

# 使用值迭代
v2 = value_iteration(env)

六、未标记样本

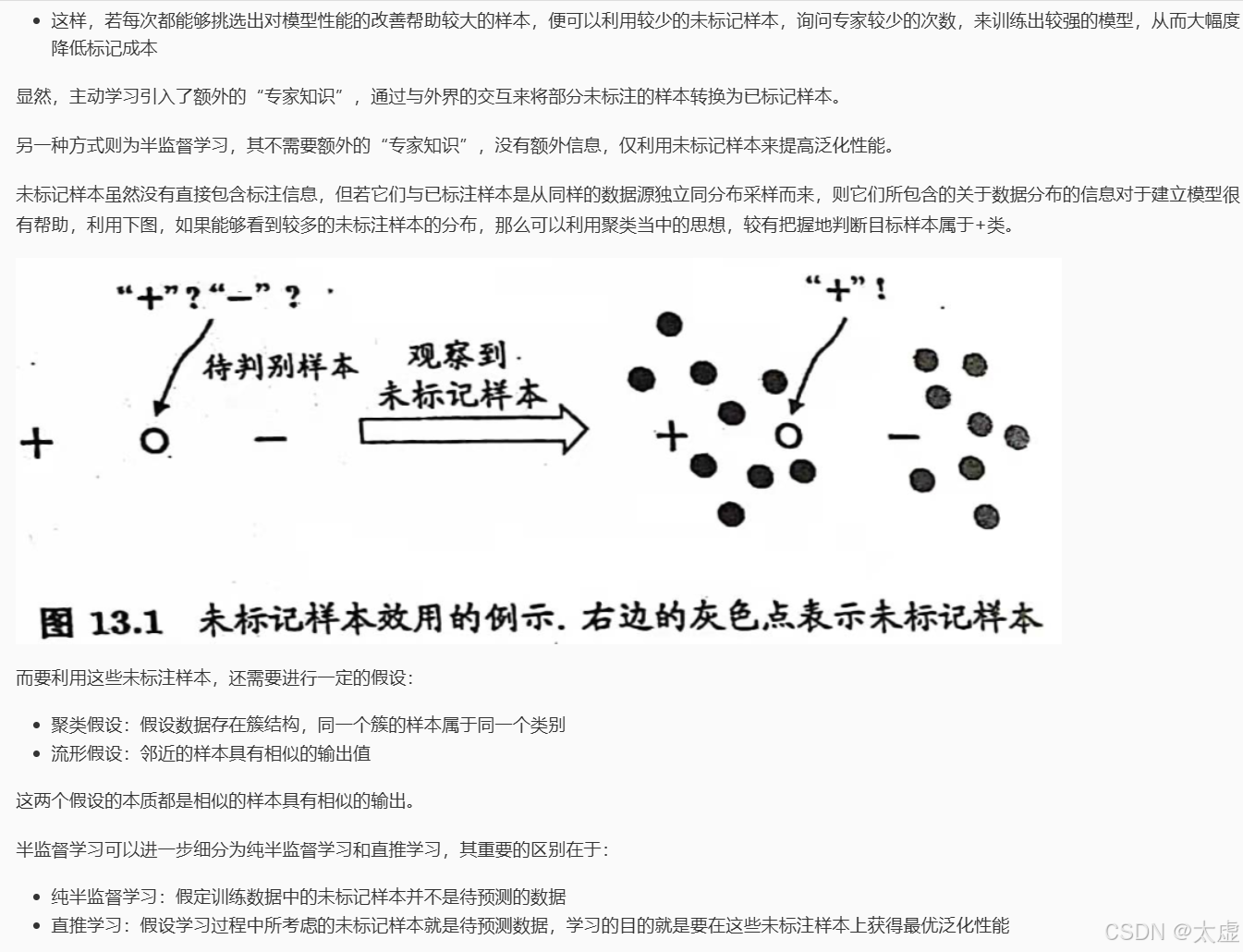
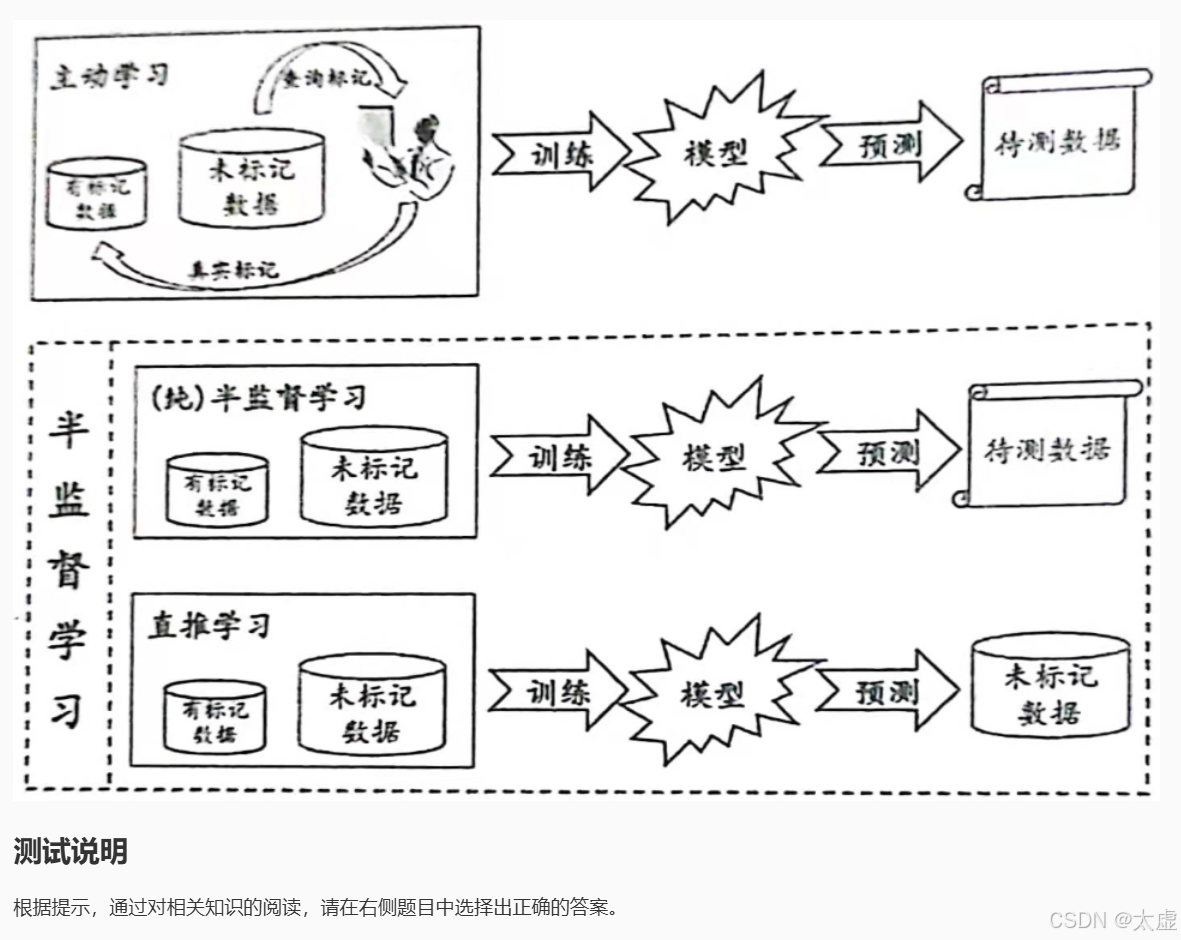
七、 生成式方法

import numpy as np  
from sklearn.datasets import make_classification  
from sklearn.semi_supervised import LabelSpreading  
from sklearn.model_selection import train_test_split  

# ********** Begin **********#
# 生成模拟数据集，生成了一个包含2000个样本和20个特征的数据集，其中只有2个特征是有信息的，10个特征是冗余的，随机种子是42。
X, y = make_classification(n_samples=2000, n_features=20, n_informative=2, n_redundant=10, random_state=42)
# ********** End **********#

# 将数据集划分为训练集和测试集  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)  
  
# 初始化模型  
lp_model = LabelSpreading(kernel="knn", alpha=0.8)  
  
# 使用有标签数据进行训练  
lp_model.fit(X_train, y_train)  
  
# 预测未标记数据的标签  
y_pred = lp_model.predict(X_test)  
  
# 输出准确率  
print("Accuracy:", np.mean(y_pred == y_test))

八、半监督SVM

import random
import numpy as np
import sklearn.svm as svm
from sklearn.datasets import make_classification
import joblib
import warnings

np.random.seed(1477)
random.seed(1477)
warnings.filterwarnings(action='ignore')


class TSVM(object):
    def __init__(self, kernel='linear'):
        self.Cl, self.Cu = 1.5, 0.001
        self.kernel = kernel
        self.clf = svm.SVC(C=1.5, kernel=self.kernel)

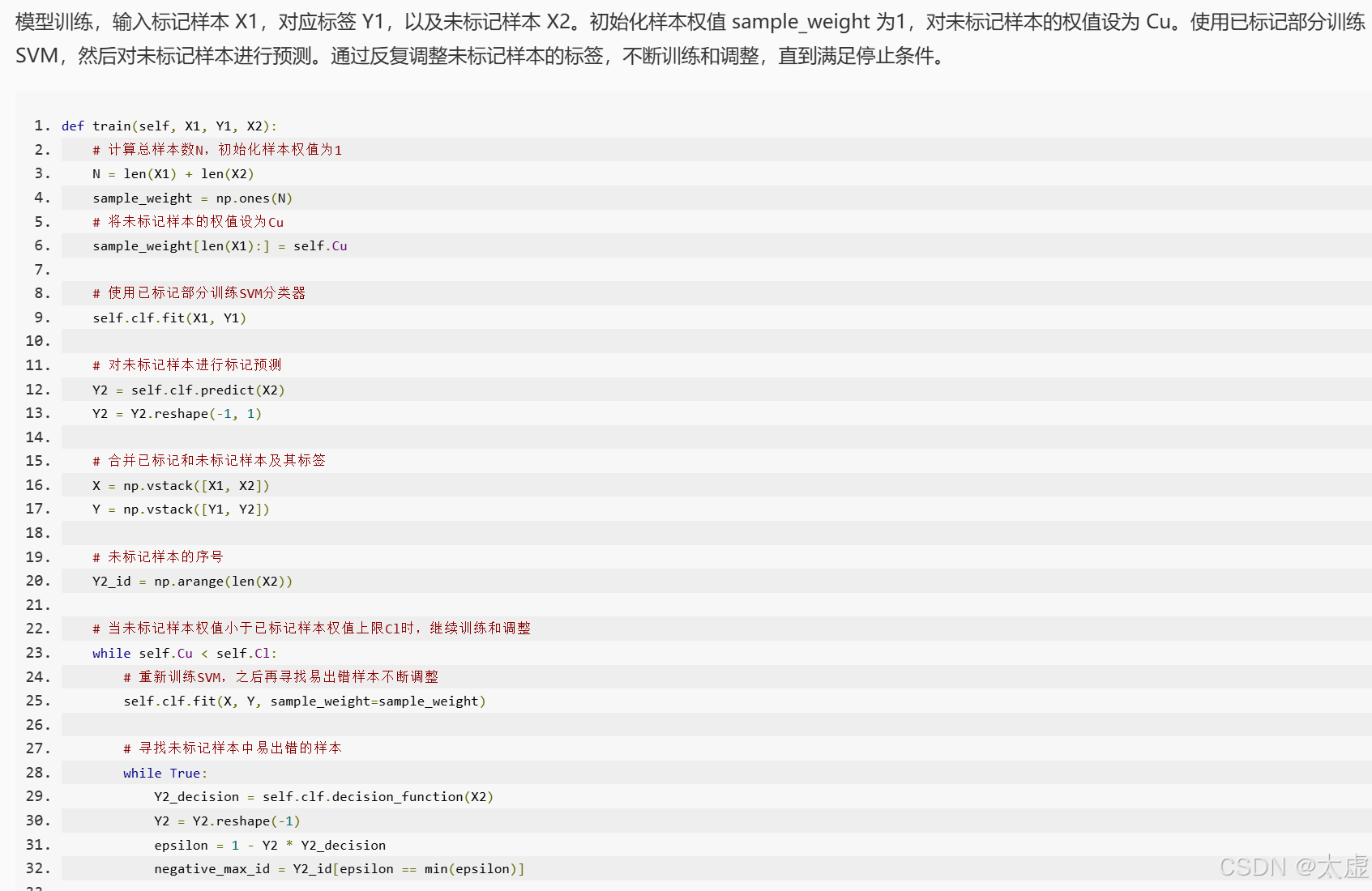
    def train(self, X1, Y1, X2):
        N = len(X1) + len(X2)
        # 样本权值初始化
        sample_weight = np.ones(N)
        sample_weight[len(X1):] = self.Cu

        # 用已标注部分训练出一个初始SVM
        self.clf.fit(X1, Y1)

        # 对未标记样本进行标记
        #********* Begin *********#
        Y2 = 
        Y2 = 

        X = 
        Y = 
        #********* End *********#

        # 未标记样本的序号
        Y2_id = np.arange(len(X2))

        while self.Cu < self.Cl:
            # 重新训练SVM, 之后再寻找易出错样本不断调整
            self.clf.fit(X, Y, sample_weight=sample_weight)
            while True:
                Y2_decision = self.clf.decision_function(X2)  # 参数实例到决策超平面的距离
                Y2 = Y2.reshape(-1)
                epsilon = 1 - Y2 * Y2_decision
                negative_max_id = Y2_id[epsilon == min(epsilon)]

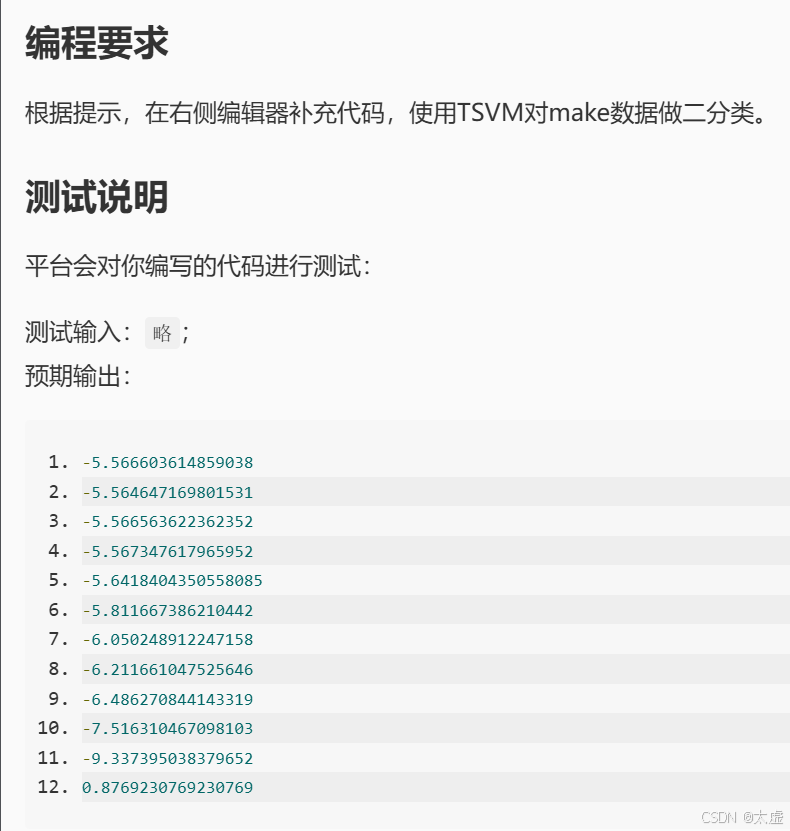
                print(epsilon[negative_max_id][0])
                if epsilon[negative_max_id][0] > 0:
                    #********* Begin *********#
                    # 寻找很可能错误的未标记样本，改变它的标记成其他标记
                    pool = 
                    Y2[negative_max_id] = 
                    Y2 = 
                    Y = 

                    self.clf.fit( )
                    #********* End *********#
                else:
                    break
            self.Cu = min(2 * self.Cu, self.Cl)
            sample_weight[len(X1):] = self.Cu

    def score(self, X, Y):
        return self.clf.score(X, Y)

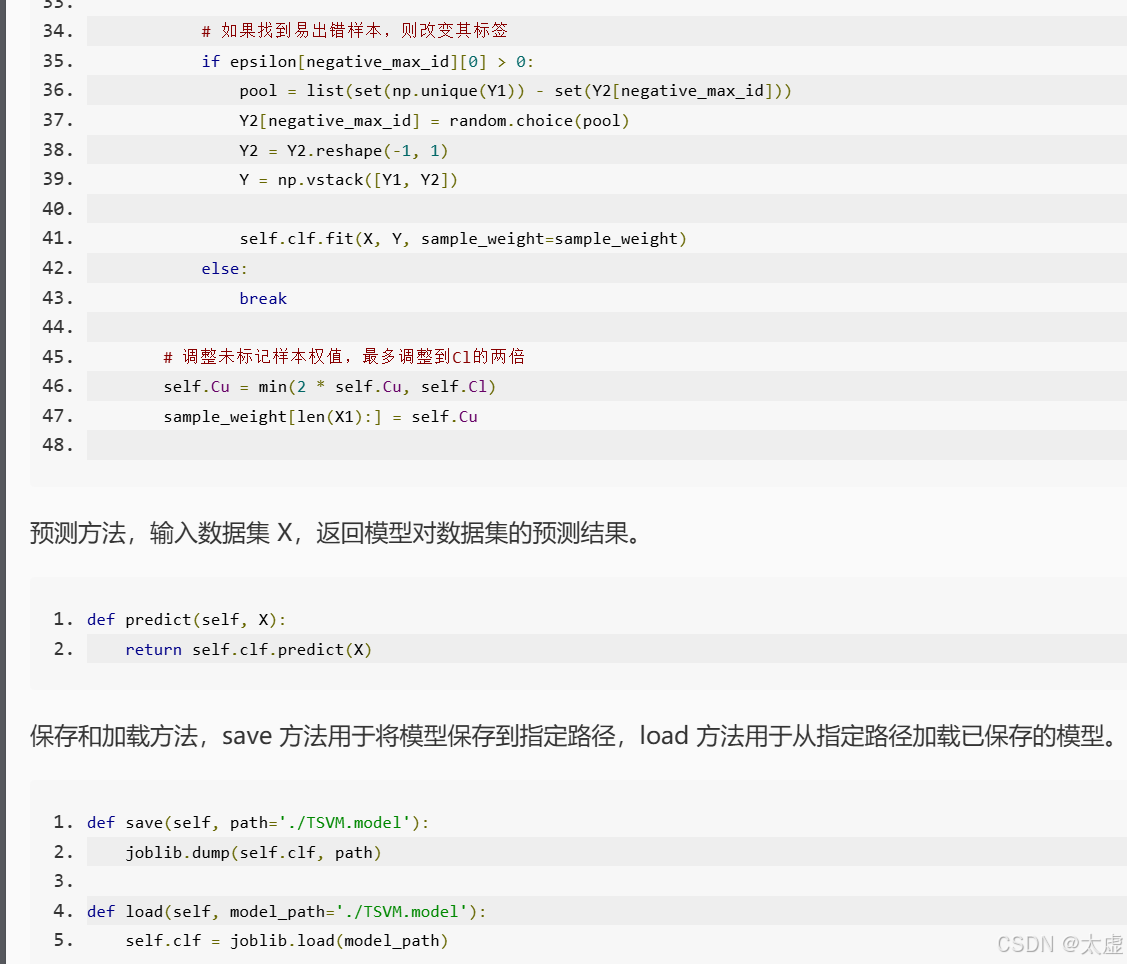
    def predict(self, X):
        return self.clf.predict(X)

    def save(self, path='./TSVM.model'):
        joblib.dump(self.clf, path)

    def load(self, model_path='./TSVM.model'):
        self.clf = joblib.load(model_path)


if __name__ == '__main__':
    features, labels = make_classification(n_samples=200, n_features=3, n_redundant=1, n_repeated=0, n_informative=2,
                                           n_clusters_per_class=2)
    n_given = 70
    # 取前n_given个数字作为标注集
    X1 = np.copy(features)[:n_given]
    X2 = np.copy(features)[n_given:]
    Y1 = np.array(np.copy(labels)[:n_given]).reshape(-1, 1)
    Y2_labeled = np.array(np.copy(labels)[n_given:]).reshape(-1, 1)

    model = TSVM()
    model.train(X1, Y1, X2)

    # Y2_hat = model.predict(X2)
    accuracy = model.score(X2, Y2_labeled)
    print(accuracy)

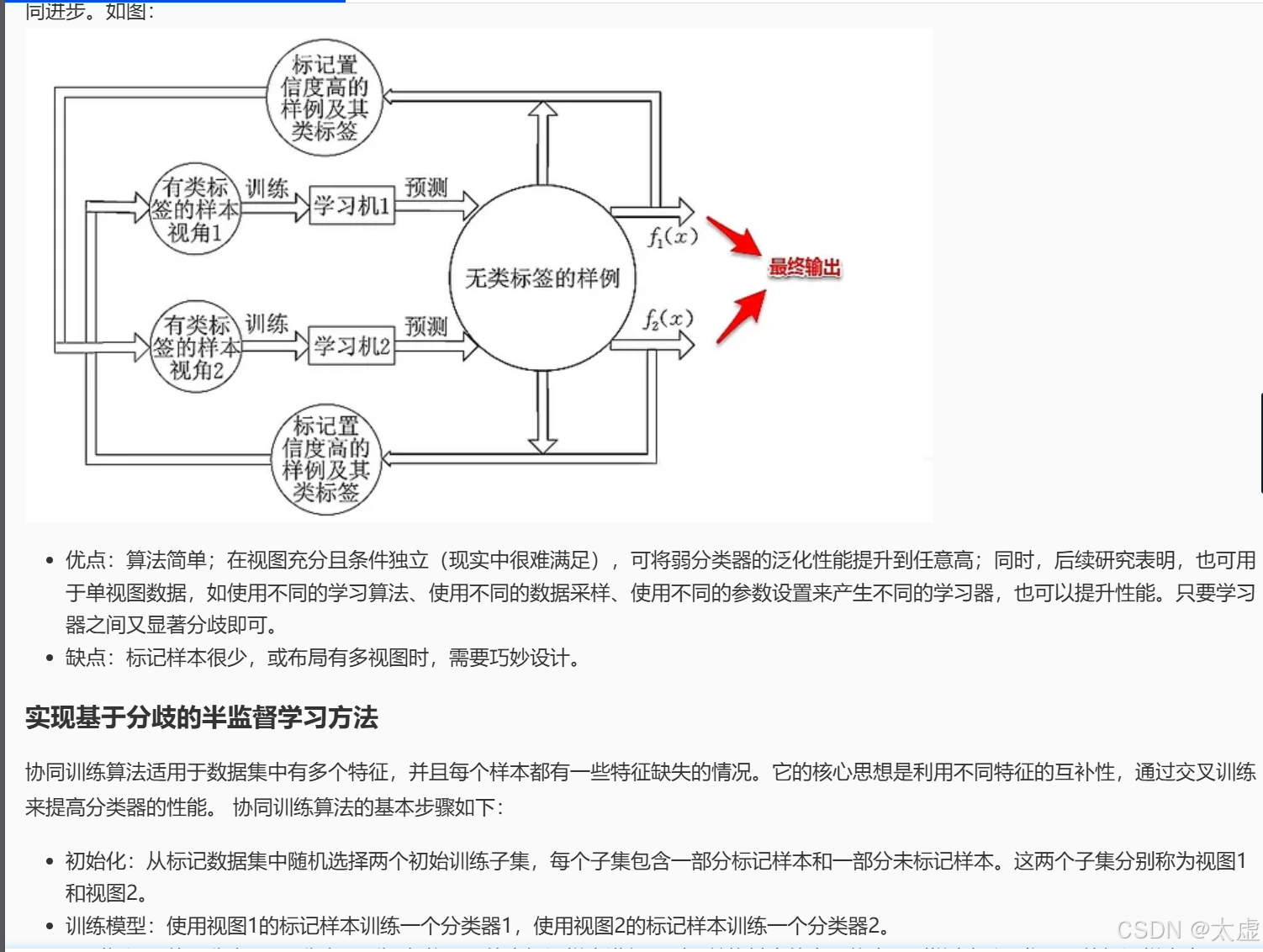
 九、基于分歧的方法

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
import numpy as np

def co_training(X, y, num_iterations):
    # ********** Begin **********#
    # 划分初始的视图1和视图2，测试集与训练集的比例为1:1， 随机种子为1。
    X_view1, X_view2, y_view1, y_view2 = train_test_split(X, y, test_size=0.5, random_state=1)
    
    # 训练两个初始分类器
    clf1 = SVC(probability=True)  # 使用probability=True以获得类别的概率值
    clf2 = SVC(probability=True)
    
    clf1.fit(X_view1, y_view1)
    clf2.fit(X_view2, y_view2)
    
    for i in range(num_iterations):
        # 使用分类器1和分类器2对未标记样本进行预测
        y_pred_view1 = clf1.predict(X_view2)
        y_pred_view2 = clf2.predict(X_view1)
        
        # 使用分类器1的高置信度预测样本来扩充视图1
        prob_view2 = clf1.predict_proba(X_view2)  # 获取预测的概率
        high_confidence_1 = np.max(prob_view2, axis=1) > 0.95  # 置信度阈值设定为0.95
        X_view1 = np.concatenate((X_view1, X_view2[high_confidence_1]))
        y_view1 = np.concatenate((y_view1, y_pred_view1[high_confidence_1]))
        
        # 使用分类器2的高置信度预测样本来扩充视图2
        prob_view1 = clf2.predict_proba(X_view1)  # 获取预测的概率
        high_confidence_2 = np.max(prob_view1, axis=1) > 0.95  # 置信度阈值设定为0.95
        X_view2 = np.concatenate((X_view2, X_view1[high_confidence_2]))
        y_view2 = np.concatenate((y_view2, y_pred_view2[high_confidence_2]))
        
        # 重新训练分类器
        clf1.fit(X_view1, y_view1)
        clf2.fit(X_view2, y_view2)
    
    # 将视图1和视图2合并为完整的训练集
    X_train = np.concatenate((X_view1, X_view2))
    y_train = np.concatenate((y_view1, y_view2))
    
    # 在完整的训练集上训练最终的分类器
    clf_final = SVC()
    clf_final.fit(X_train, y_train)
    
    return clf_final
    # ********** End **********#

# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target

# 使用协同训练算法进行分类
clf = co_training(X, y, num_iterations=5)

# 在测试集上进行预测
X_test = X[100:]  # 使用后50个样本作为测试集
y_test = y[100:]
y_pred = clf.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

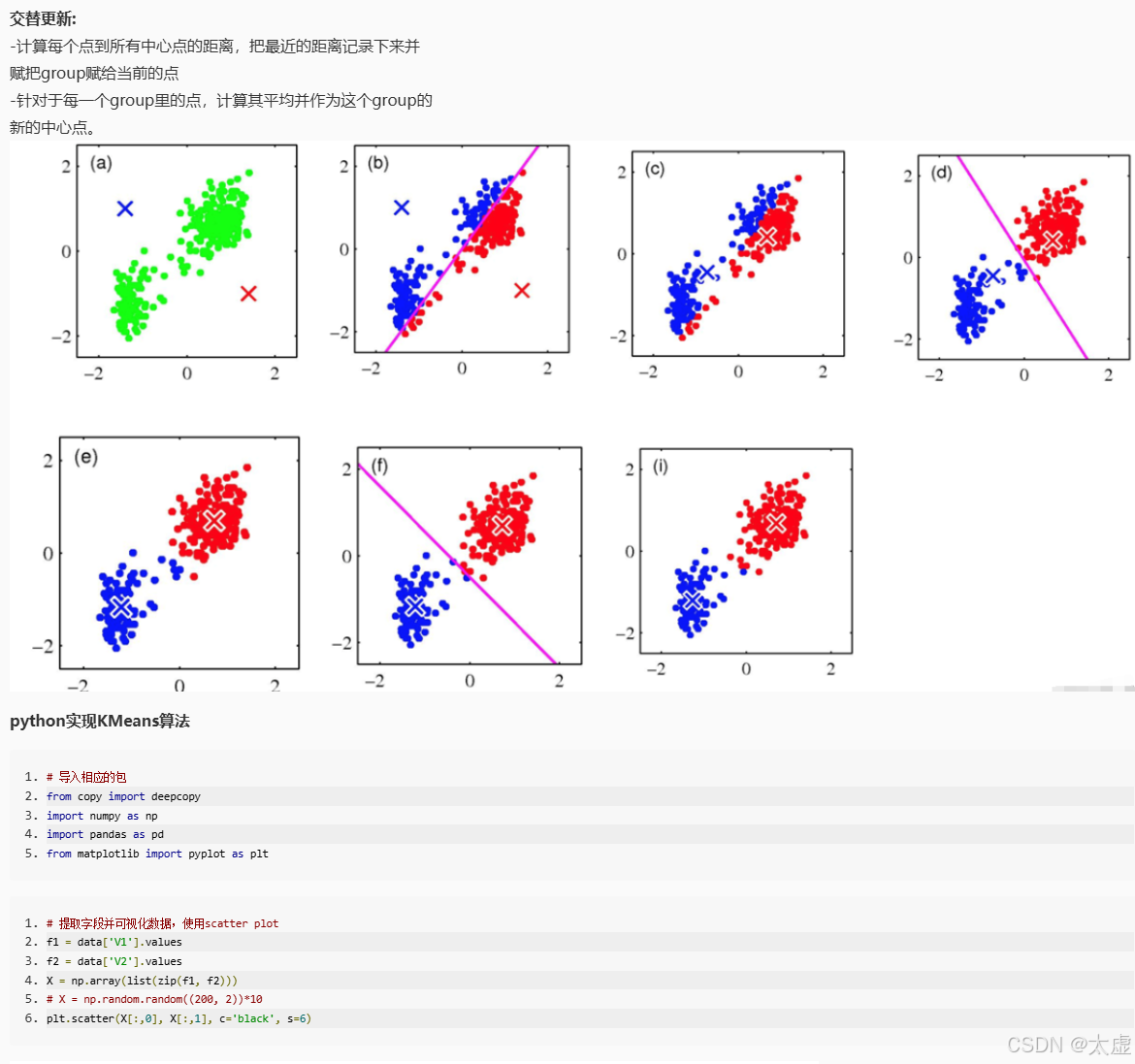
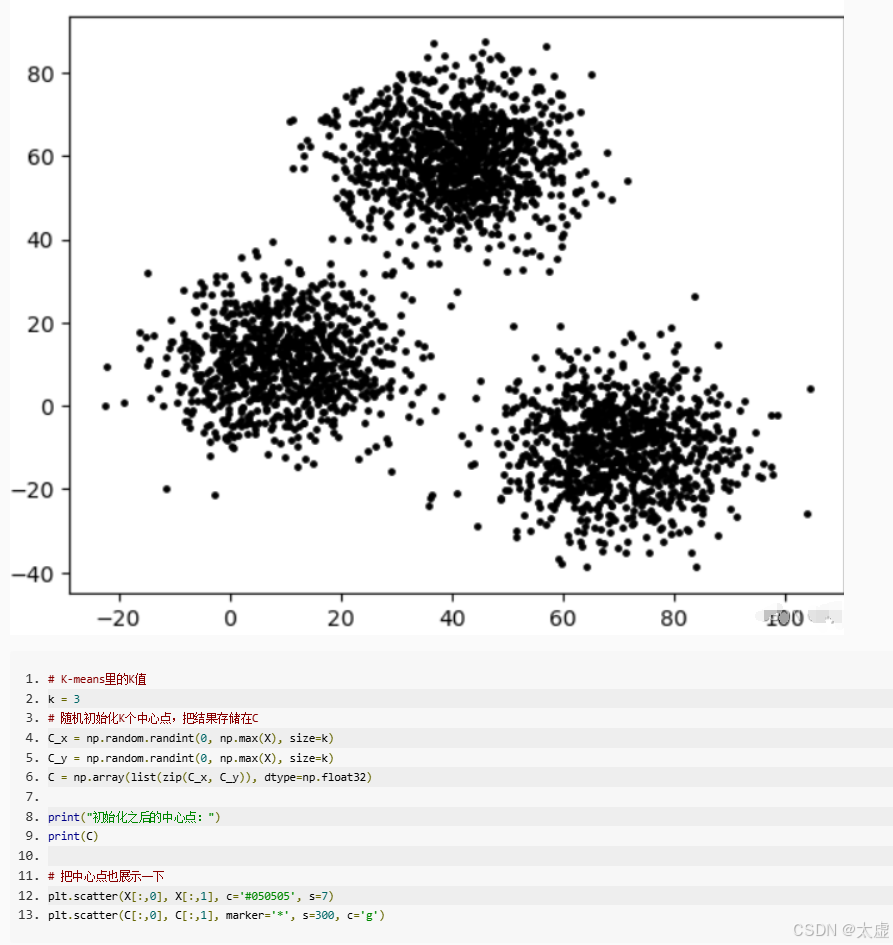
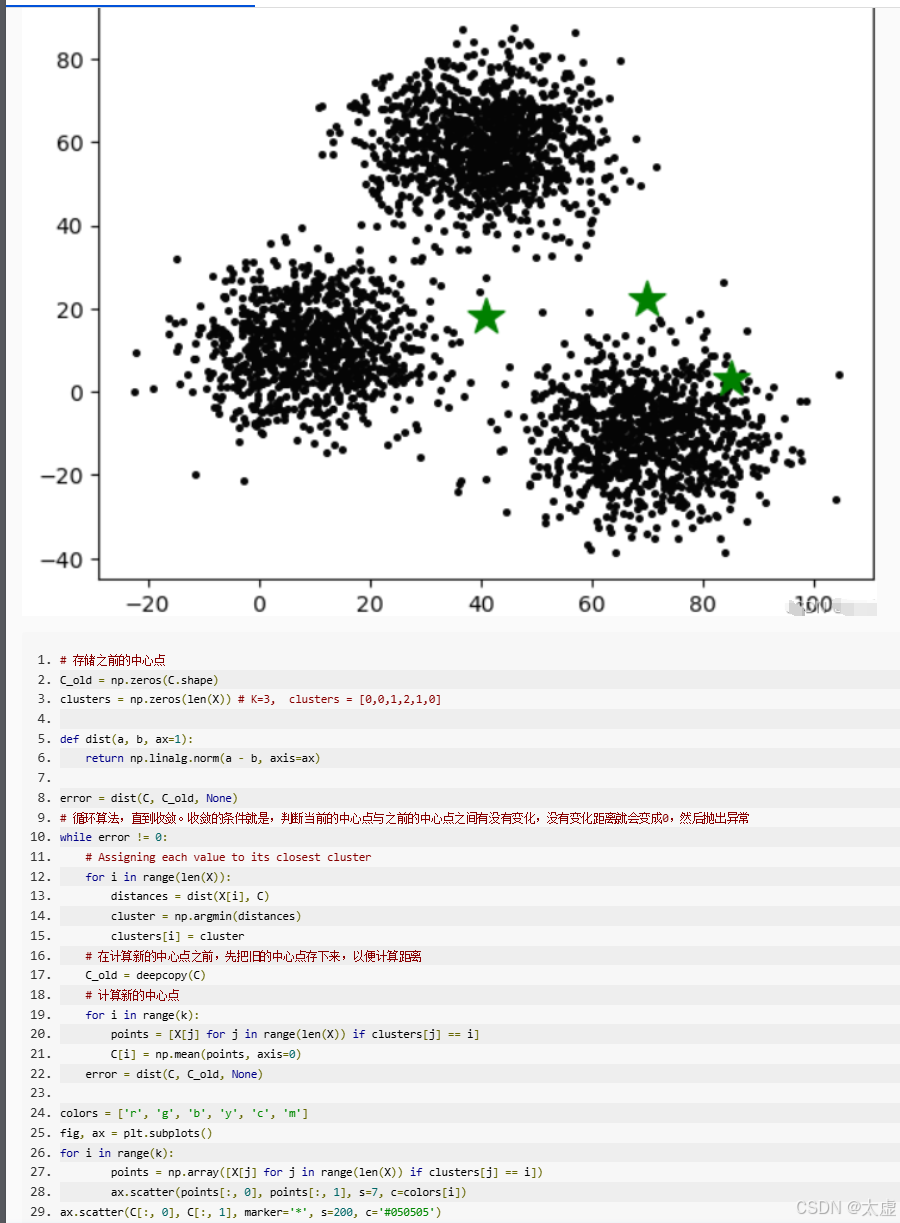
十、半监督聚类

import numpy as np

def distEclud(vecA, vecB):
    '''
    输入：向量A和B
    输出：A和B间的欧式距离
    '''
    return np.sqrt(sum(np.power(vecA - vecB, 2)))

def newCent(L):
    '''
    输入：有标签数据集L
    输出：根据L确定初始聚类中心
    '''
    centroids = []
    label_list = np.unique(L[:, -1])  # 获取所有的类别标签
    for i in label_list:
        L_i = L[(L[:, -1]) == i]  # 按照标签分割数据
        cent_i = np.mean(L_i, 0)  # 计算每个簇的均值
        centroids.append(cent_i[:-1])  # 忽略最后一列标签
    return np.array(centroids)

def semi_kMeans(L, U, distMeas=distEclud, initial_centriod=newCent):
    '''
    输入：有标签数据集L（最后一列为类别标签）、无标签数据集U（无类别标签）
    输出：聚类结果
    '''
    # 合并有标签数据L和无标签数据U
    dataSet = np.vstack((L[:, :-1], U))  # L去掉标签，U本身无标签
    label_list = np.unique(L[:, -1])     # 获取L中所有类别标签
    k = len(label_list)                  # L中类别个数
    m = np.shape(dataSet)[0]             # 数据集总共有多少样本
    
    # 初始化样本分配（记录每个点的聚类标签）
    clusterAssment = np.zeros(m)
    centroids = initial_centriod(L)      # 确定初始聚类中心
    clusterChanged = True

    while clusterChanged:
        clusterChanged = False
        # 1. 将每个样本分配到最近的聚类中心
        for i in range(m):
            minDist = np.inf  # 初始化最小距离为无穷大
            minIndex = -1
            for j in range(k):
                dist = distMeas(dataSet[i], centroids[j])  # 计算样本i到聚类中心j的距离
                if dist < minDist:
                    minDist = dist
                    minIndex = j  # 找到最近的聚类中心
            if clusterAssment[i] != minIndex:  # 如果该样本的标签发生了变化
                clusterChanged = True
            clusterAssment[i] = minIndex  # 更新该样本的标签
        
        # 2. 更新聚类中心
        for j in range(k):
            # 获取当前簇中所有样本
            pointsInCluster = dataSet[clusterAssment == j]
            if len(pointsInCluster) > 0:
                newCentroid = np.mean(pointsInCluster, axis=0)  # 计算该簇样本的均值
                centroids[j] = newCentroid  # 更新聚类中心
    
    return clusterAssment

# 测试数据
L = np.array([[1.0, 4.2, 1],
              [1.3, 4.0, 1],
              [1.0, 4.0, 1],
              [1.5, 4.3, 1],
              [2.0, 4.0, 0],
              [2.3, 3.7, 0],
              [4.0, 1.0, 0]])  # L的最后一列是类别标签

U = np.array([[1.4, 5.0],
              [1.3, 5.4],
              [2.0, 5.0],
              [4.0, 2.0],
              [5.0, 1.0],
              [5.0, 2.0]])

# 执行半监督K-means
clusterResult = semi_kMeans(L, U)
print(clusterResult)