【伪随机数】关于排序算法自测如何生成随机数而引发的……
以 Random 开始
可能一开始,你只是写到了排序算法如何生成随机数
public static void main(String[] args) {
Random random = new Random();
int[] nums = new int[10];
for (int i = 0; i < nums.length; i++) {
nums[i] = random.nextInt(100);
}
System.out.println("Before sorting...");
for (int num : nums) {
System.out.println(num);
}
quickSort(nums, 0, nums.length - 1);
System.out.println("After sorting...");
for (int num : nums) {
System.out.println(num);
}
}然后想弱弱的问一句
Random random = new Random();
int num = random.nextInt(100);num的取值范围包不包括 100?
然后,你看到了这篇文章~恭喜🎉~你以后再也不会忘记什么是伪随机数了
(什么、你并不想知道什么是伪随机数?……emmm来都来了,花一分钟瞅瞅呗_
一切都起源于这张图
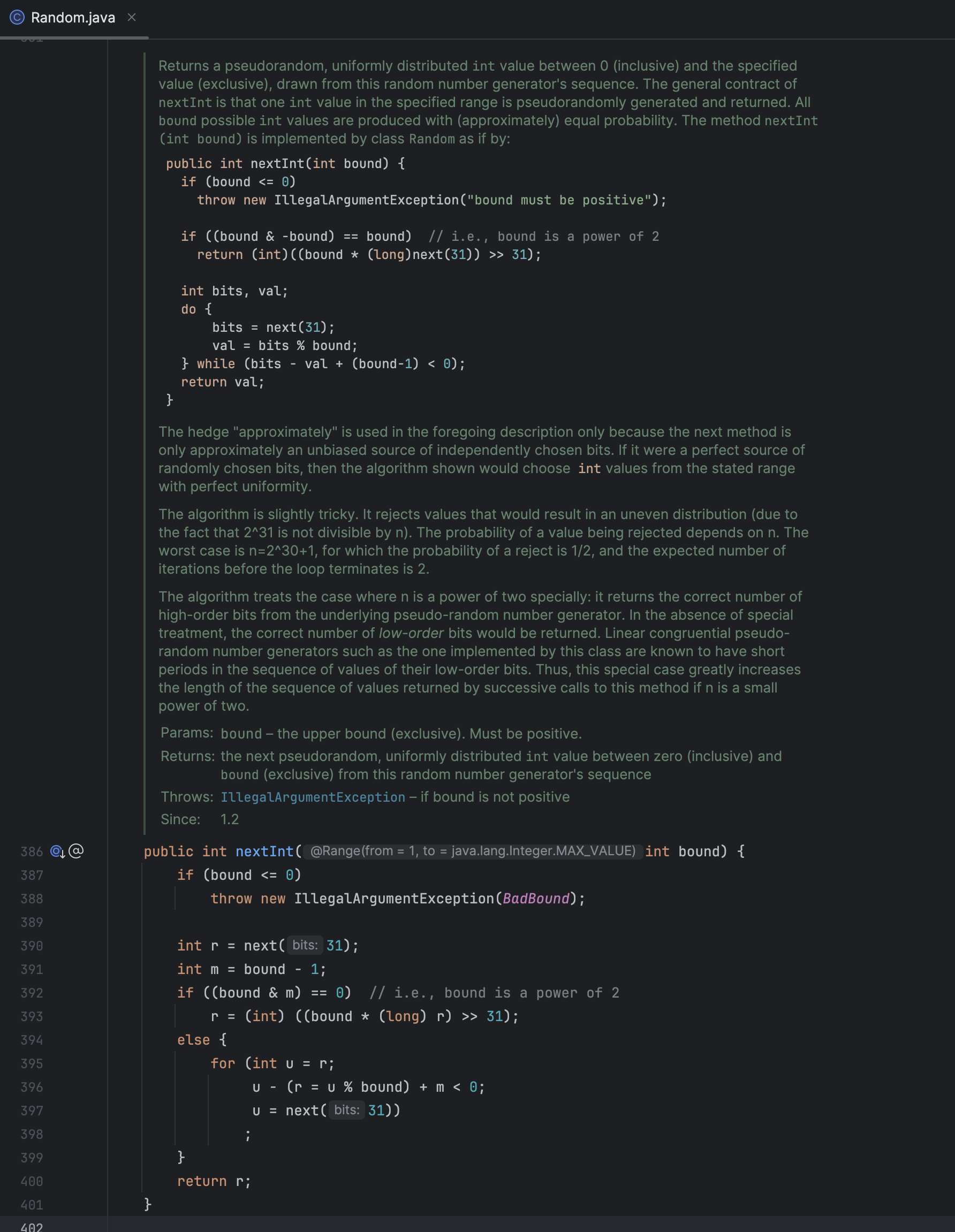
我们大致翻译下上面👆的注释
返回一个介于 0(包含)和指定值(不包含)之间的伪随机(pseudorandom)、均匀分布的 int 值,该值取自随机数生成器的序列。
nextInt 的一般约定是在指定范围内伪随机生成并返回一个 int 值。
所有绑定的 int 值都会以(近似)相等的概率生成。
……
“伪随机”?“(近似)相等的概率”?什么意思 为什么这么说我们 random 生成的随机数?
什么是伪随机数(pseudorandom)?
伪随机数就是由算法生成的随机数,真随机是真正随机的数。
emmmm...哈哈约等于没说哈
其实一般来讲,计算机生成的的都叫伪随机数,因为他们都有以下几点共同之处:
- 算法可重现性:比如我们开篇引入内容提到的Random函数,它其实就是通过确定性的数学算法来生成随机数的,即只要给定相同的初始值(种子),就会按照固定的规则和步骤,产生完全相同的随机数序列(比如常见的伪随机数生成算法线性同余发生器(LCG))
- 缺乏真正的不确定性:真正的随机数来源于自然界的随机事件,如放射性衰变、热噪声等,这些事件是不可预测的,具有真正的不确定性。正如上一个特性“算法可重现性”提到的,只要知道初始值和规则,就可以重现整个随机数序列,所以它并不是真正的不确定(只是我们无法简单的确定下一个是啥)。而真正的随机数,如基于量子随机数生成器产生的随机数,其每一个数值的出现都是独立的、不可重现的随机事件的结果。
为什么量子随机数生成器产生的就是真正的随机数?
大家应该有听过那个“薛定谔的猫”吧%%
这是一个著名的思想实验,在这个思想实验中,一只猫被放置在一个密封的盒子里,盒子内有一个装有毒气的装置,该装置与一个放射性原子相连。根据量子力学的解释,在未进行观测之前,放射性原子处于衰变与未衰变的叠加态,相应地,猫也处于既死又活的叠加态。只有当我们打开盒子进行观测时,原子的波函数才会坍缩,猫的状态才会确定为死或活。
而量子随机数生成器中的量子比特(qubit)也处于类似的叠加态,直到被测量才会塌缩到0或1的某个确定状态,且塌缩到0或1的概率是相等的,这种不确定性是量子力学的基本特性,不是由任何外部因素或人为设定的算法所决定的,因此基于量子叠加态的测量结果具有真正的随机性。
- 周期性重复:虽然现代的伪随机数生成算法周期通常很长很长很长长长长……但理论上它们生成的随机数序列终究会重复。例如,梅森旋转算法的周期为2的19937次方减1,虽然这个周期非常长,在一般应用中几乎不会出现重复的情况,但从理论上讲,当生成的随机数数量达到这个周期时,序列就会开始重复。
梅森旋转算法(Mersenne Twister,MT19937)的周期到底有多长?
2^19937-1(2的19937次方减1),其实不是很有概念,这个数到底有多大?
宇宙有多大知道不emmmm
目前观测到的宇宙直径约为930亿光年,即9.3 × 10^10光年
换算成米为:
9.3 × 10^10 × 9.461 × 10^15 ≈ 8.8 × 10^26 米
那么2^19937米相当于多少个宇宙直径?
2^19937 / 8.8 × 10^26 ≈ 4.89×10^5974
相当于 4.89×10^5974 个宇宙直径
宇宙不太熟悉?那用地球算算。。。
地球的赤道周长约为40,075公里,即40,075,000米。
2^19937(2的19937次方)米相当于多少个地球周长?
简单除一下……2^19937/40,075,000 约等于1.07×10^5994
相当于绕地球赤道大约1.07×10^5994圈
以 Random 结束
我们回到一开始的问题:
Random random = new Random();
int num = random.nextInt(100);num的取值范围包不包括 100?
不包括嘿嘿😊
[0,100) 左闭右开,就是函数注释中的第一句
返回一个介于 0(包含)和指定值(不包含)之间的伪随机(pseudorandom)、均匀分布的 int 值,该值取自随机数生成器的序列。
